[Nächstes Kapitel] [vorangehendes Kapitel] [vorangehendes Kapitel (SeitenEnde)] [SeitenEnde] [Inhalt]
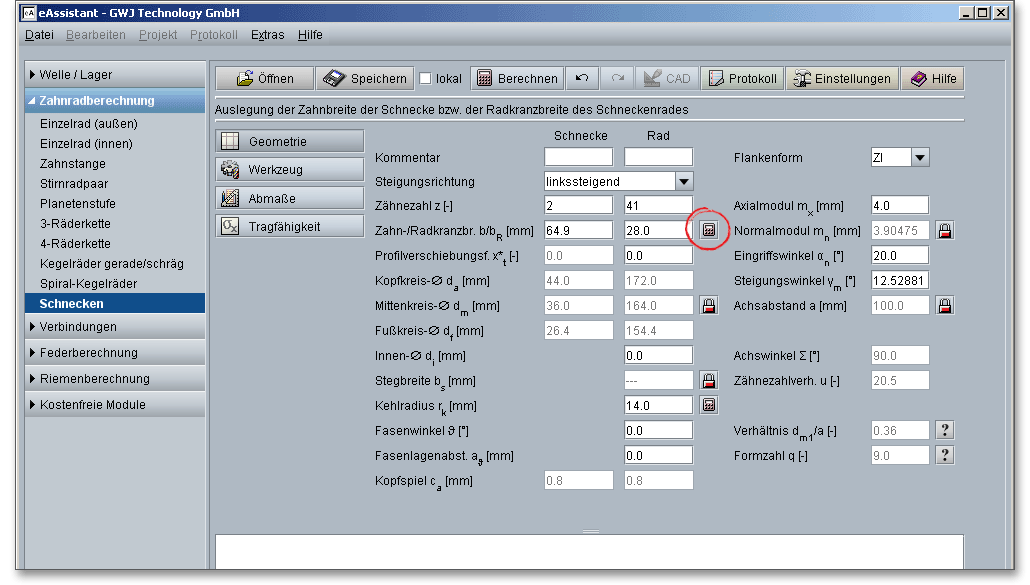
Melden Sie sich auf der Startseite www.eAssistant.eu mit Ihrem Benutzernamen und Ihrem Passwort an. Um das Berechnungsmodul für Schnecken zu starten, klicken Sie in der Baumstruktur auf der linken Seite auf den Menüpunkt „Zahnradberechnung“ und anschließend auf „Schnecken“.

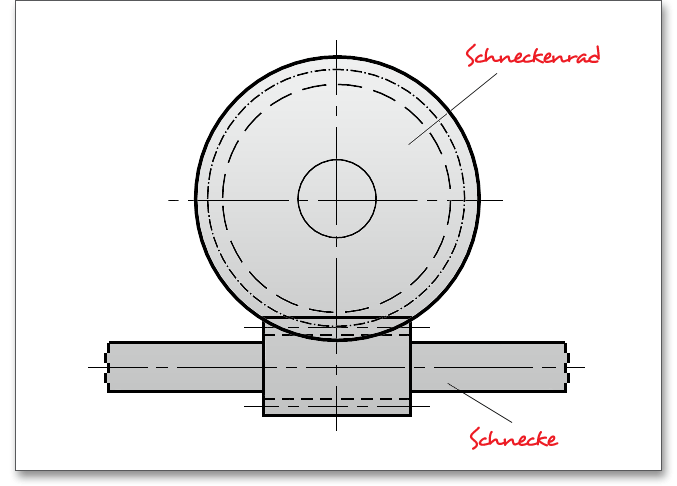
Dieses Modul ermöglicht eine einfache und schnelle Berechnung der Geometrie und Festigkeit von
zylindrischen Schnecken in Verbindung mit einem Globoidrad. Die Schnecke weist eine zylindrische Form auf,
das dazu gehörige Schneckenrad eine globoidische Form. In industriellen Anwendungen wird diese Bauform
am häufigsten verwendet. Das Schneckengetriebe ist ein Sonderfall der Schraubradgetriebe und dient zum
Übertragen von Drehbewegungen und Drehmomenten. Da sich die Zahnflanken der Schnecke und des
Schneckenrades linienförmig berühren, erhöht sich die Flankentragfähigkeit und die Schneckengetriebe
laufen somit ruhiger und geräuschärmer als Schraubgetriebe. Sie dienen für große Übersetzungen ins
Langsame und ins Schnelle. Üblicherweise hat die Schnecke einen kleineren Durchmesser als das
Schneckenrad. Zwischen der Achse der Schnecke und des Schneckenrades besteht meist ein Achswinkel von
90\(^\circ \). Der Zahneingriff von Schnecke und Schneckenrad ist vergleichbar mit dem Zahneingriff von Zahnstange
und Stirnrad.
Zu den wesentlichsten Eigenschaften der Schneckengetriebe gehören:
Die Geometrieberechnung erfolgt nach DIN 3975. Die Tragfähigkeitsberechnung erfolgt nach DIN 3996
Methode B, ISO/TR 14521 Methode B oder nach Niemann. In dem Modul werden verschiedene Flankenformen
unterstützt. Bei der Berechnung werden zum Beispiel Profilverschiebung am Rad oder die Toleranzen
berücksichtigt.
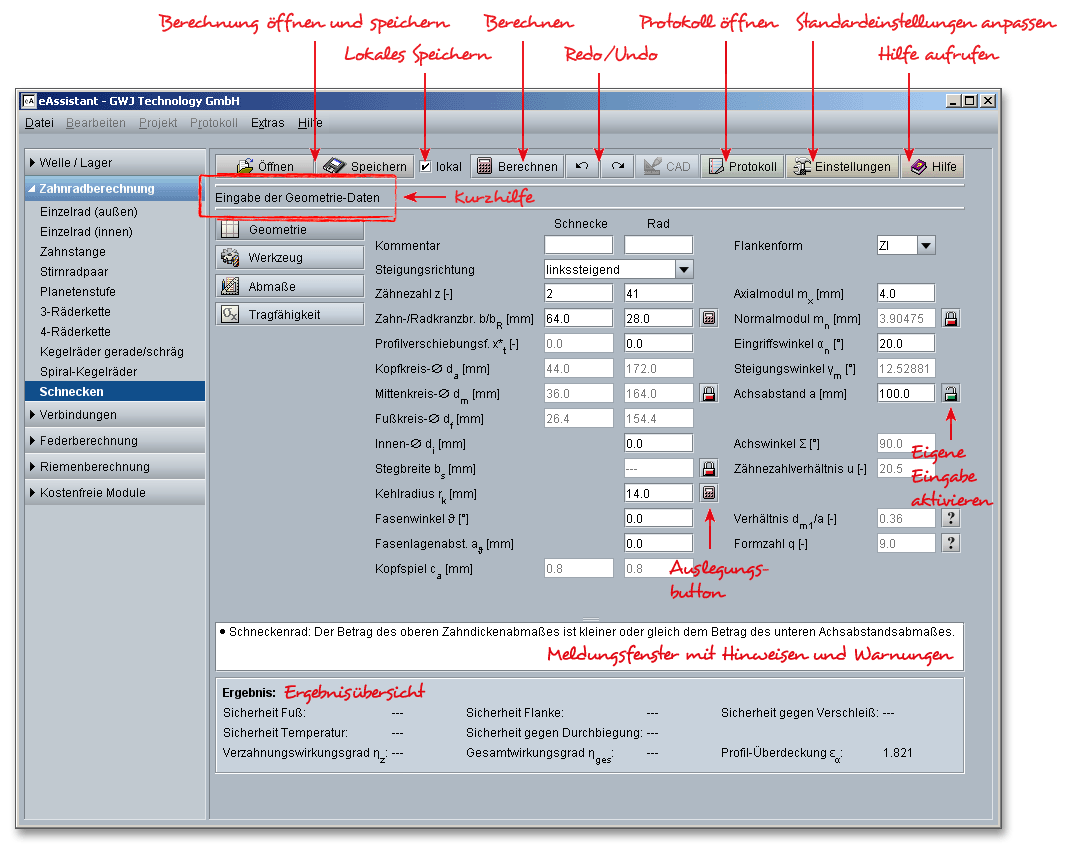
Die Ergebnisse werden bereits während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld angezeigt.
Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Dadurch werden jegliche Veränderungen
der Eingabewerte auf die Ergebnisse schnell sichtbar. Werden die Mindestsicherheiten nicht erfüllt, so wird das
Ergebnis mit einer roten Markierung angezeigt. Grundsätzlich können Sie jede Eingabe mit der Enter-Taste
oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können Sie mit der Tab-Taste durch
die Eingabemaske springen oder nach jeder Eingabe auf den Button „Berechnen“ klicken. Auch
hierbei werden die Werte entsprechend übernommen und die Ergebnisse sofort in der Übersicht
angezeigt.
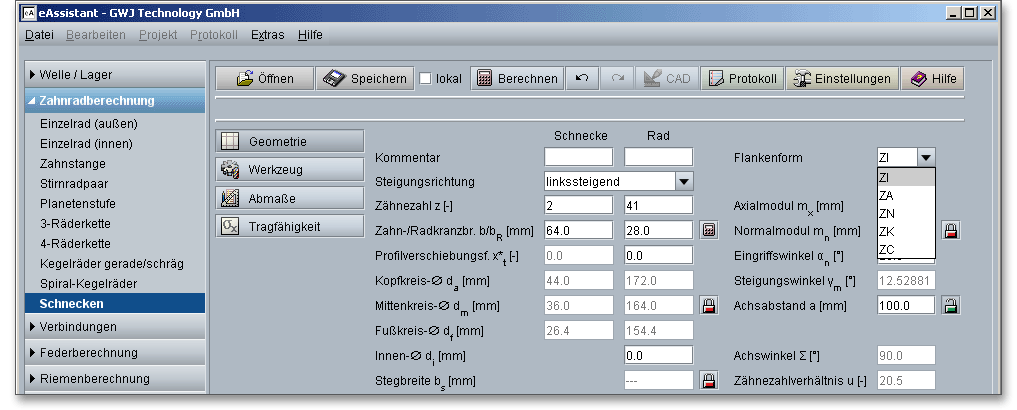
Je nach Herstellungsverfahren ergeben sich an den Zylinderschnecken verschiedene Flankenformen, die nach DIN 3975 genormt sind. Wegen ihrer Wirtschaftlichkeit in der Herstellung mit geradflankigen Schleifscheiben werden am häufigsten die Flankenformen ZI und ZK verwendet. Die ZA-, ZK-, ZN- und ZI-Schnecken unterscheiden sich in ihrer Tragfähigkeit, Schmierdruckbildung und der Verlustleistung nur geringfügig. Aus der Listbox lassen sich die verschiedenen Flankenformen auswählen.
Die Schneckenzahnflanken sind wie bei Schrägstirnrädern Evolventenflächen. Die Schnecke heißt
deswegen auch Evolventenschnecke, die Kennzeichnung I steht für Involute. Die Profilerzeugung erfolgt mit
einem Drehmeißel oder Wälzfräser.
Die Schneckengänge der ZA-Schnecke sind im Axialschnitt gerade (trapezförmig). Diese Flankenform
entsteht, wenn ein trapezförmiger Drehmeißel so angestellt wird, dass die Schneiden im Axialschnitt
liegen.
Die ZN-Schnecke weist in einem Normalschnitt durch die Mitte einer Zahnlücke ein gerades Flankenprofil auf.
Im Axialschnitt ist das Flankenprofil leicht konkav. Die Herstellung erfolgt mit einem schräg angestellten
Drehmeißel oder einem kleinen trapezförmigen Scheibenfräser.
Die ZK-Schnecke weist ein konvexes Axialschnittprofil auf, das mit einem rotierenden scheibenförmigen Werkzeug mit trapezförmigem Profil erzeugt wird. Die Herstellung kann mit einer Schleifscheibe erfolgen, deren Achse um den Steigungswinkel \(\gamma _{m}\) am Mittenkreis gegenüber der Schneckenachse gedreht ist. Die Balligkeit der Flanken hängt vom Durchmesser des Werkzeugs ab.
Wenn Sie diese Flankenform aus der Listbox auswählen, dann gibt es in der Maske „Werkzeug“ eine Eingabemöglichkeit für den Schleifscheibendurchmesser \(d_{mS0}\).
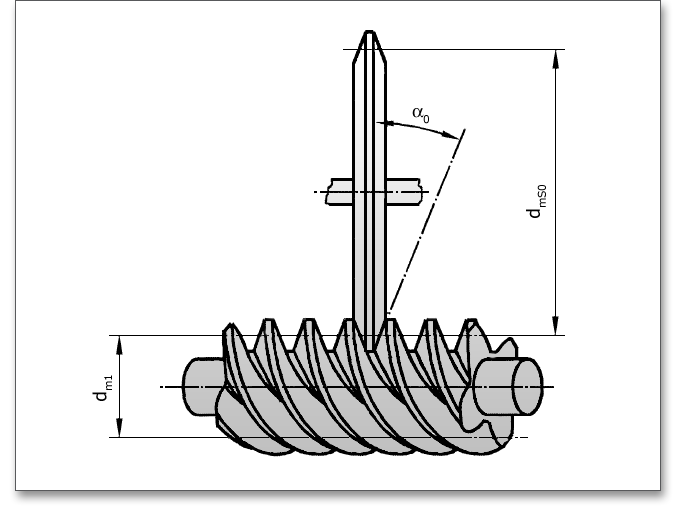
Bei der Flankenform C sind die Schneckenflanken im Axialschnitt konkav gekrümmt. Die Herstellung kann mit
einer Schleifscheibe erfolgen, deren Achse um den Steigungswinkel \(\gamma _{m}\) am Mittenkreis gegenüber
der Schneckenachse gedreht ist. Die Schleifscheibe weist ein Kreisbogenprofil mit dem Radius \(\varrho _{0}\)
auf.
Je nach Flankenrichtung unterscheidet man rechts- und linkssteigende Schnecken. Eine Schnecke ist rechtssteigend (linkssteigend), wenn die geschraubte Flankenlinie einer Rechtsschraube (Linksschraube) entspricht.
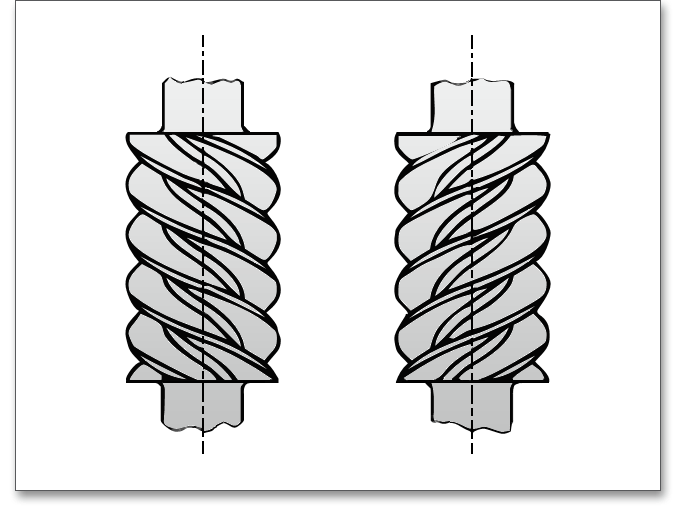
Üblich sind rechtssteigende Schnecken. Die Flankenrichtung einer Schneckenradverzahnung ergibt sich aus der Flankenrichtung der dazugehörigen Schnecke, die Flankenrichtung des Schneckenrades ist also mit der zugehörigen Schnecke identisch. Schnecke und Schneckenrad besitzen die gleiche Flankenrichtung. Daher wird ein rechtssteigendes (linkssteigendes) Schneckenrad stets mit einer rechtssteigenden (linkssteigenden) Schnecke gepaart.
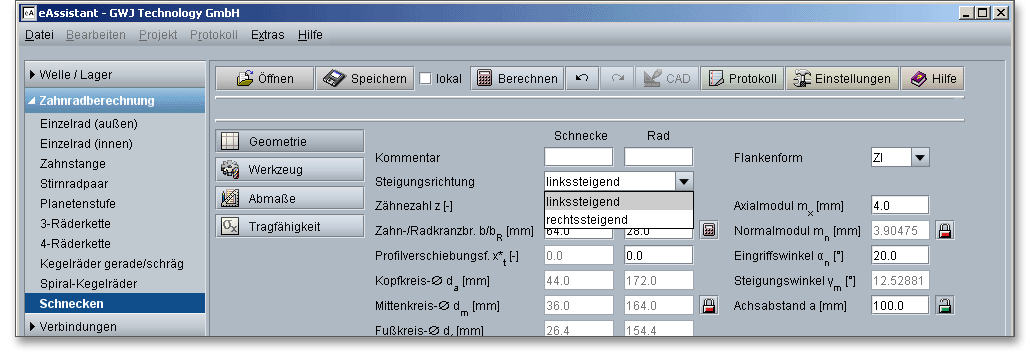
Schnecken haben einen oder mehrere Zähne, die wie Gänge von Schrauben unter gleichbleibender
Steigung um die Schneckenachse gewunden sind. Die Zähnezahl \(z_{1}\) der Schnecke ist die Anzahl der in
einem Stirnschnitt geschnittenen Zähne. Die Zähnezahl bewegt sich üblicherweise im Bereich 1 \(\le z_{1} \le \)
4.
Das Modul \(m_{x}\) bezieht sich auf den Axialschnitt der Schnecke bzw. auf den Stirnschnitt des Schneckenrades. An einer Schnecke sind die Zahnprofile im Axialschnitt, im Normalschnitt und im Stirnschnitt von Bedeutung. Der Schnitt durch die Schnecke in einer Ebene, die die Schneckenachse enthält, ergibt einen Axialschnitt der Schnecke. Der Schnitt durch die Schneckenverzahnung senkrecht zur Schneckenachse ergibt einen Stirnschnitt der Schnecke. Der Schnitt durch die Schnecke senkrecht zu einer Mittenzylinder-Flankenlinie ergibt den Normalschnitt der Schnecke. In Schneckenradsätzen hat die Schnecke den Axialmodul \(m_{x}\), das Schneckenrad den Stirnmodul \(m_{t}\). Bei \(\Sigma \) = \(90^\circ \) ist \(m_{x} = m_{t} = m\). Axialmodul der Schnecke und Stirnmodul des Schneckenrades sind identisch. Bei Drehung der Schnecke bewegen sich deren Zähne axial wie eine Zahnstange.
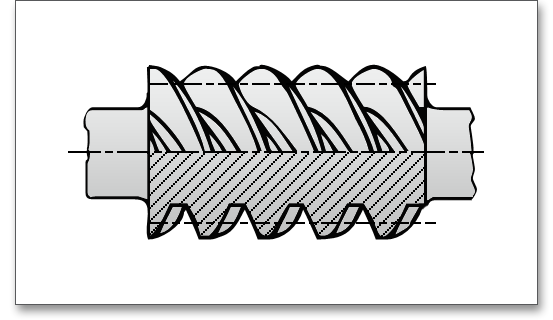
Die Berechnung im eAssistant ist mit beliebigen Modulen, auch mit mehreren Nachkommastellen, möglich. Klicken Sie auf die Beschriftung des Eingabefeldes für den Axialmodul, so lässt sich alternativ Diametral und Circular Pitch eingeben und umrechnen.
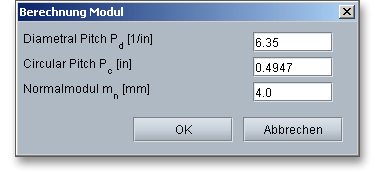
Sie haben bei der Berechnung auch die Möglichkeit, den Normalmodul \(m_{n}\) anstatt des Axialmoduls zu verwenden. Aktivieren Sie dazu den Schloss-Button, um das Eingabefeld freizuschalten. Geben Sie einen Wert für den Normalmodul ein. Das Eingabefeld für den Axialmodul wird dabei deaktiviert. Die Berechnung mit dem Normalmodul beeinflusst den Kopf- und Fußkreis.
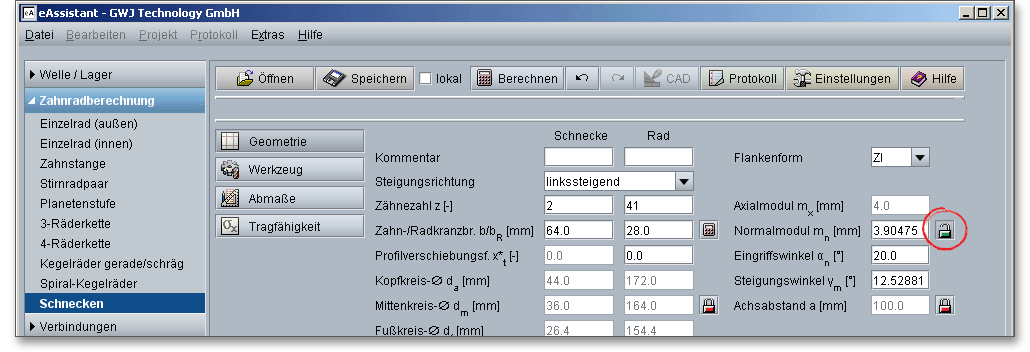
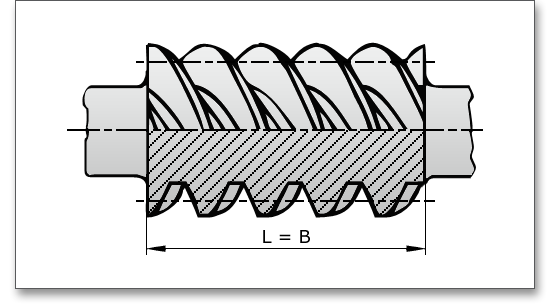
Die Verzahnungslänge ist der Abstand zweier Stirnschnitte, zwischen denen die Zahnflanken vollständig ausgebildet sind.
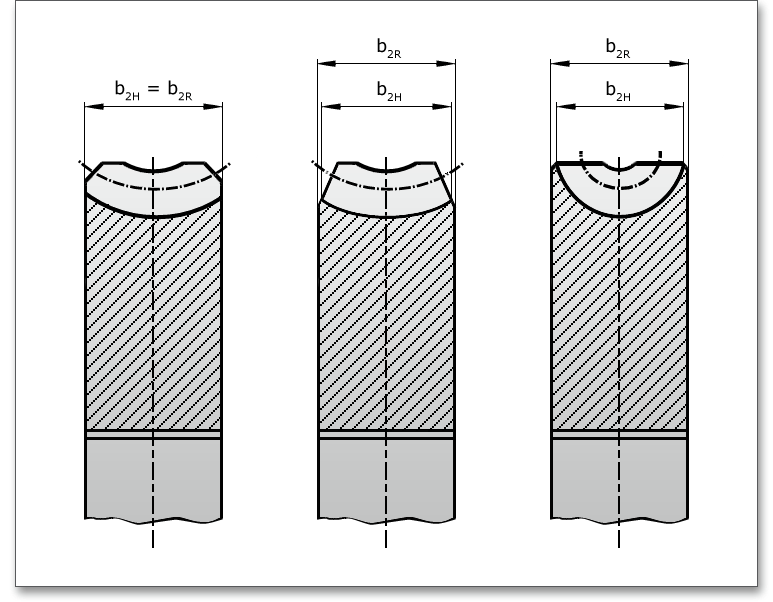
Die Bemaßung der Schnecke zeigt die folgende Abbildung. Der Wert für \(b_{R}\) (\(b_{R} = b_{2R}\)) wird im Eingabefeld vorgegeben, es berechnen sich daraus \(b_{2H}\) und \(b_{2}\).
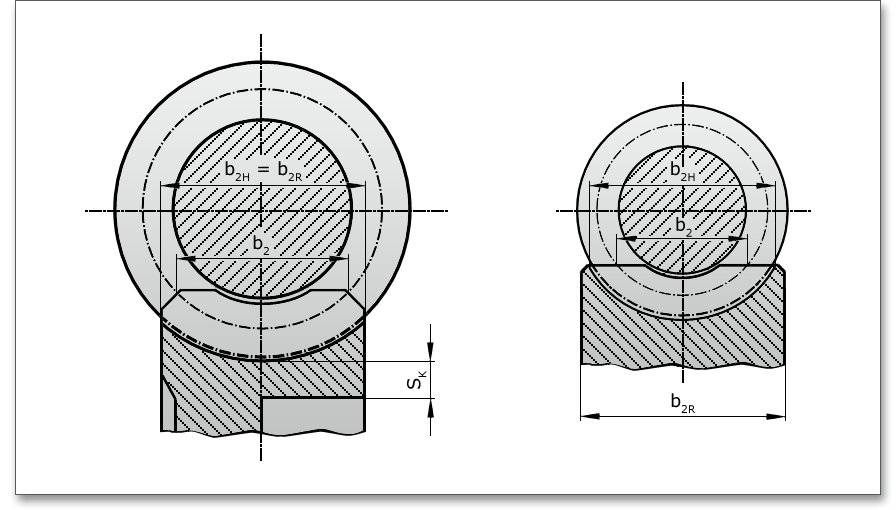
Um die Zahnbreite der Schnecke bzw. die Radkranzbreite des Schneckenrades zu optimieren, klicken Sie auf das Taschenrechner-Symbol.
Als Profilverschiebung am Schneckenrad ist der radiale Abstand zwischen dem Mantel des Mittenzylinders der
Schnecke und dem Teilkreis des Schneckenrades zu verstehen. Vorzugsweise ist der Profilverschiebungsfaktor \(x \geq 0\)
zu wählen. Negative Profilverschiebungen sollten möglichst vermieden werden. Da eine Zahnstange (=
Axialschnitt der Schnecke) durch Profilverschiebung nicht verändert wird, kann nur das Schneckenrad eine
Profilverschiebung erhalten.
Empfehlungen für den Profilverschiebungsfaktor (nach Niemann):
Für den Eingriffswinkel im Normalschnitt wird \(\alpha _{n}\) = 20\(^\circ \) empfohlen. Öffnen Sie das Berechnungsmodul, dann ist
standardmäßig ein Eingriffswinkel von 20\(^\circ \) eingestellt.
Der Steigungswinkel \(\gamma _{m}\) am Mittenkreis ist der spitze Winkel zwischen einer Tangente an einer Mittenzylinder-Flankenlinie und einer Stirnschnittebene. Der Steigungswinkel der Schnecke ist gleich dem Schrägungswinkel des Schneckenrades \((\gamma _{m} = \beta _{m})\).
Der Mittenzylinder wird als Bezug für die Bestimmungsgrößen an einer Schnecke verwendet. Der Mittenkreisdurchmesser kann nach konstruktiven Gesichtspunkten frei gewählt werden.
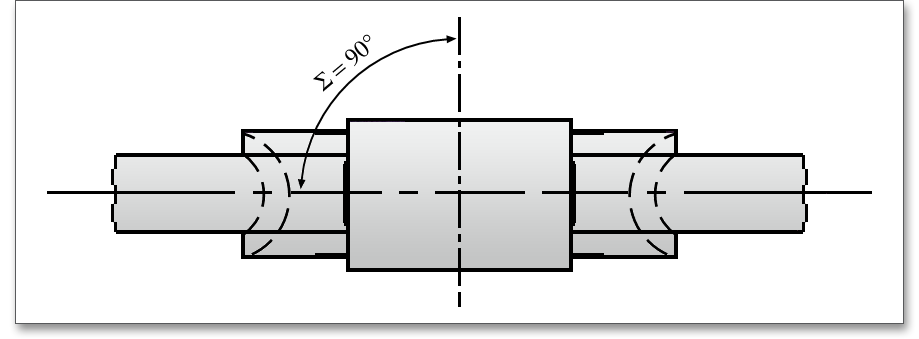
Der Achsabstand \(a\) ist der kürzeste Abstand zwischen beiden Radachsen. Die Achsen von Schnecke und Schneckenrad kreuzen sich bei großem Achsabstand, meist unter 90\(^\circ \). Andere Achsenwinkel sind eher selten.
Die Breite eines Steges kann hier berücksichtigt werden. Es besteht für Sie die Möglichkeit, die Stegbreite über den Schloss-Button zu verändern. Noch ist der Schloss-Button deaktiviert. Geben Sie einen Innendurchmesser für das Schneckenrad in dem entsprechenden Eingeabefeld ein, dann aktiviert sich der Schloss-Button und die Stegbreite wird zunächst auf den gleichen Wert wie die Radkranzbreite des Schneckenrades gesetzt. Über den Schloss-Button kann jetzt die Stegbreite individuell angepasst werden.

Das Zähnezahlverhältnis \(u\) ist das Verhältnis der Zähnezahl \(z_2\) des Schneckenrades zur Zähnezahl \(z_{1}\) der Schnecke. Das Zähnezahlverhältnis ist gleich dem Betrag der Übersetzung \(i = n_{1}/n_{2}\) als Verhältnis der Drehzahlen. Es sind folgende Zähnezahlen \(z_{1}\) der Schnecke üblich:
| \(i\) | 5...10 | 10...15 | 15...30 | > 30 |
| \(z_{1}\) | 4 | 3 | 2 | 1 |
Der Kehlradius \(r_{k}\) ist der Radius des Erzeugungskreises der Kehlkopffläche.
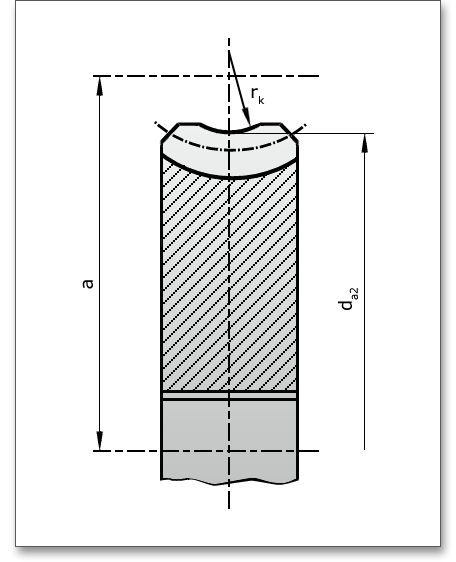
Hier haben Sie die Möglichkeit, den Kehlradius des Schneckenrades auszulegen bzw. zu optimieren. Um den Kehlradius auszulegen, klicken Sie einfach auf das Taschenrechner-Symbol.

Der Fasenwinkel einer Schneckenverzahnung ist der Winkel zwischen den verlängerten Fasen des Radzahnes. Der Fasenlagenabstand bezeichnet den Abstand vom Schnittpunkt der verlängerten Fasen zur Schneckenradachse. Beide Größen lassen sich individuell festlegen.
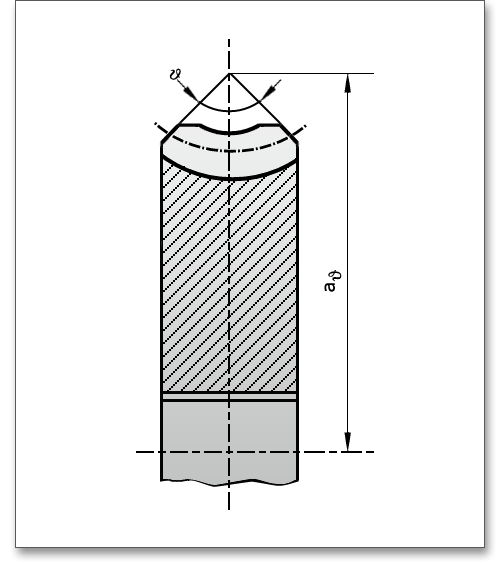
Das Kopfspiel der Schnecke ist der Abstand zwischen dem Zahnkopf der Schnecke und dem Zahnfuß des Schneckenrades. Das Kopfspiel des Schneckenrades ist der Abstand zwischen dem Zahnkopf des Schneckrades und dem Zahnfuß der Schnecke.
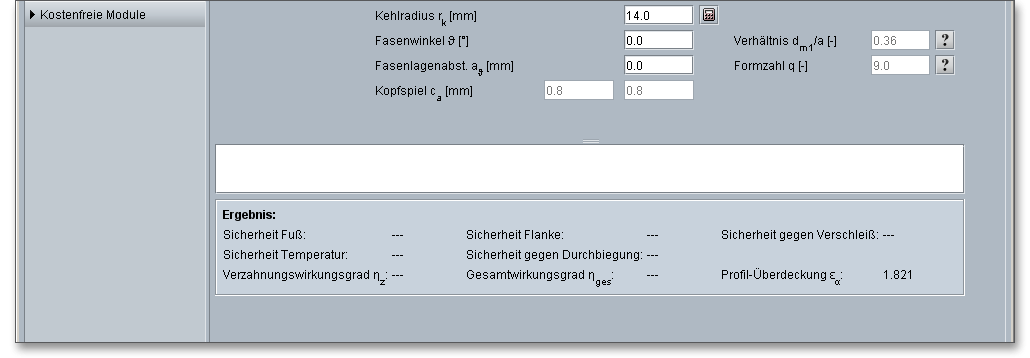
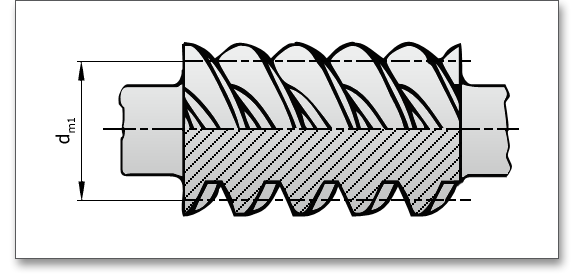
Ein Klick auf den Fragezeichen-Button öffnet eine Abbildung anhand derer sich die Wahl des Durchmesser-Achsabstandsverhältnis \(d_{m1}/a\) bestimmen lässt. Mit zunehmenden \(d_{m1}/a\) erhöhen sich die Sicherheiten gegen Grübchenbildung und Durchbiegung, aber auch der Verzahnungswirkungsgrad und Temperatursicherheit fällt. Hinsichtlich eines möglichst hohen Wirkungsgrads strebt man ein kleines \(d_{m1}/a\) an, jedoch ist dabei die Durchbiegung zu beachten (Gefahr von Zahneingriffsstörungen).

Die Formzahl \(q\) stellt das Verhältnis des Mittenkreisdurchmessers zum Axialmodul dar und kennzeichnet die Gestalt der Schnecke und damit ihr Widerstandsmoment gegen Durchbiegung. Üblicherweise werden Schnecken mit einer Formzahl von \(q\) = 6 bis 17 verwendet, im Mittel \(q\) = 10. Kleine Formzahlen vergrößern \(\gamma _{m}\), führen aber zu dünnen, nicht sehr biegesteifen Schnecken. Ist die Formzahl hoch, dann wird \(\gamma _{m}\) kleiner und die Schnecke damit kräftiger. Neben dem Feld finden Sie einen Fragezeichen-Button. Klicken Sie dort, dann öffnet sich ein neues Fenster mit zusätzlichen Informationen zum Formfaktor.
Die Herstellung des Rades erfolgt meist mit einem Fräser, der die Form der Schnecke hat. Das bedeutet, dass das Schneckenrad nicht mit anderen Schnecken gepaart werden kann. Die Schneckenflankenformen ZA, ZN und ZK können auf der Drehbank geschnitten werden (Einzelteilfertigung). Bei Kleinserien benutzt man Scheibenfräser und Schneidräder (Schälen). Mehrgängige Evolventenschnecken können auf Wälzfräsmaschinen verzahnt werden. Kleine Schnecken werden oft fertiggerollt. Genauigkeitsschnecken werden fertiggeschliffen, wobei Profilschleifen wegen der höheren Wirtschaftlichkeit bevorzugt wird.
Hinweis: Wie schon im Bereich der Geometrieeingabe haben Sie auch hier die Möglichkeit, bei Schnecke und
Schneckenrad jeweils eine Bemerkung oder eine kurze Beschreibung hinzuzufügen.
Die folgenden genormten Werkzeug-Bezugsprofile stehen Ihnen für die Berechnung zur Verfügung und können über die Listbox ausgewählt werden:
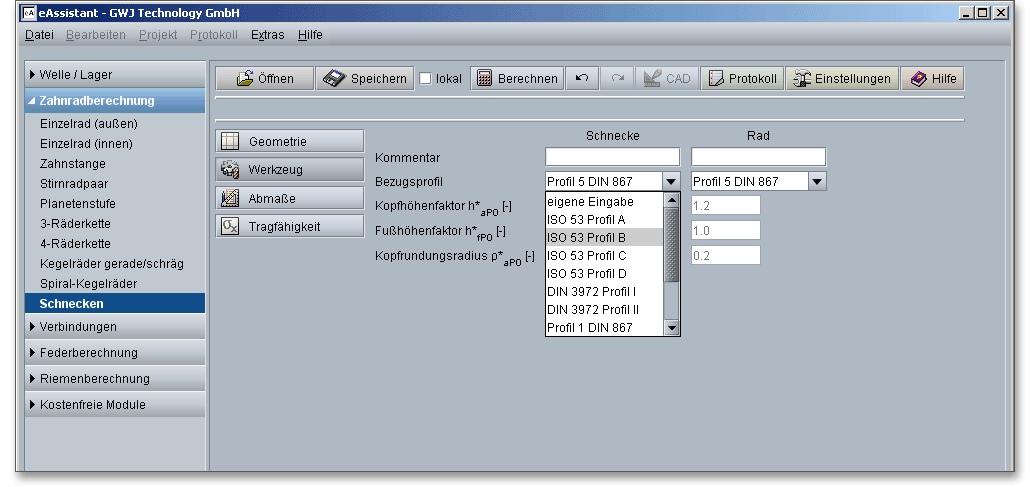
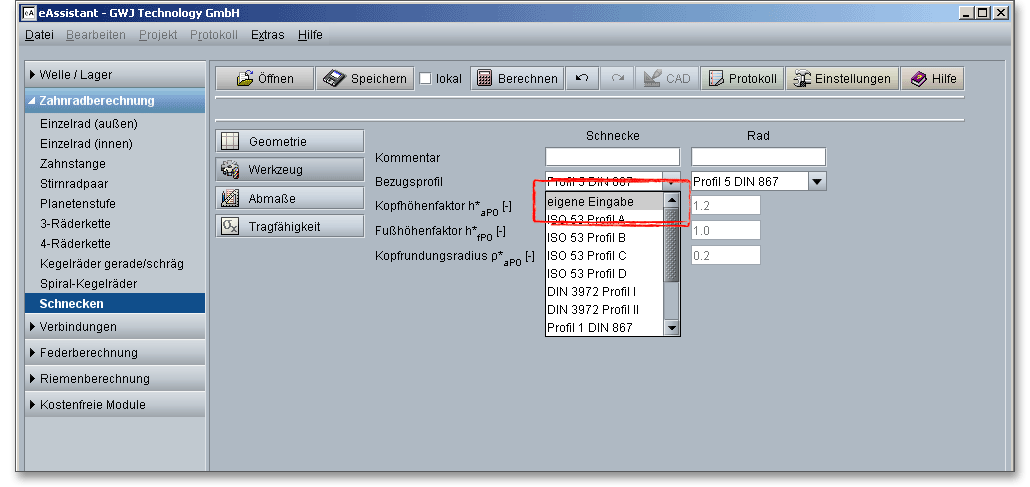
Wenn Sie in der Listbox „eigene Eingabe“ wählen, werden der Kopfrundungsradius, die Kopfhöhe und die Fußhöhe aktiviert. Sie können so schnell das Werkzeug-Bezugsprofil individuell vorgeben.
Eine Herstellung von Werkstücken mit exakten Nennmaßen ist unmöglich. Wie schon bei Stirnradverzahnungen müssen auch bei Schneckengetrieben Abweichungen vom theoretischen Sollmaß zugelassen werden. Für die Paarung von Schnecke und Schneckenrad sind Abmaße vom spielfreien Zustand erforderlich, um das nötige Flankenspiel zu erreichen. Allgemein erfordern Schneckengetriebe ein größeres Flankespiel als gerad- oder schrägverzahnte Stirnräder, weil die Schnecke aus Stahl und das Schneckenrad aus Schleuderbronze hergestellt werden und in einem Gussgehäuse gelagert werden. Die oft hohen Gleitgeschwindigkeiten erzeugen erhebliche Temperaturerhöhungen, die zu unterschiedlicher Ausdehnung der verschiedenen Werkstoffe führen und so eine Änderung des Flankenspiels verursachen.
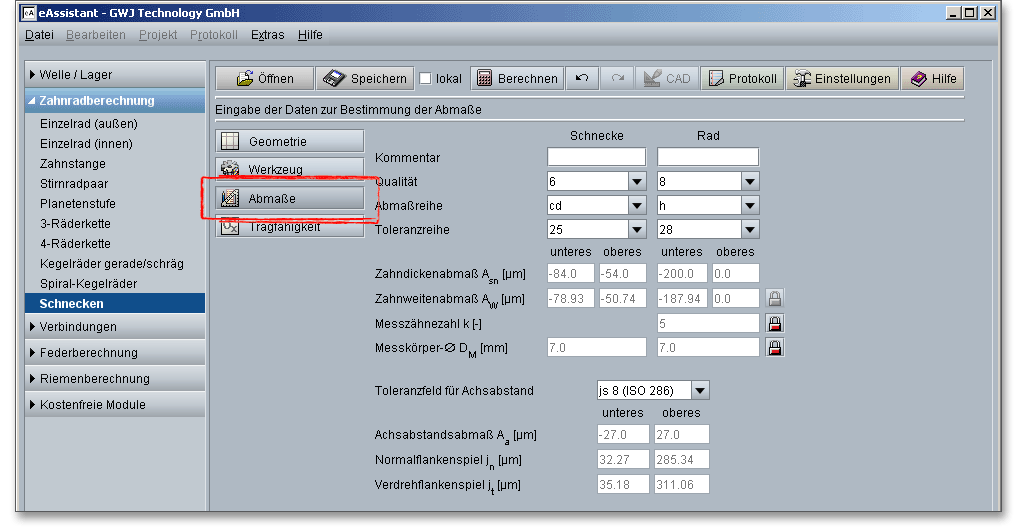
Die Qualität ist nach wirtschaftlichen Gesichtspunkten in Abhängigkeit vom Verwendungszweck und somit vom Fertigungsverfahren festzulegen. In den DIN-Verzahnungsnormen werden die qualitativen Grenzen für die einzelnen Abweichungen in 12 Verzahnungsqualitäten festgelegt und in der Reihenfolge der Genauigkeit von 12 bis 1 bezeichnet. Die Qualität 1 bezeichnet dabei die feinste Genauigkeit, die Qualität 12 die gröbste Genauigkeit. Die feineren Verzahnungsqualitäten sind z.Z. fertigungstechnisch nicht erreichbar.
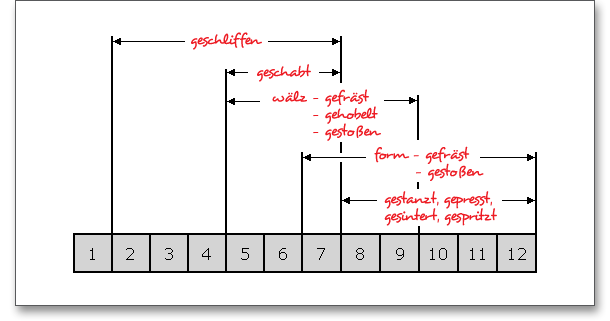
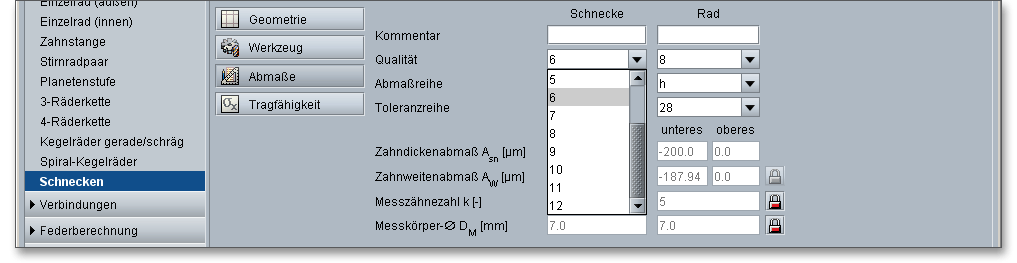
Wählen Sie im Berechnungsmodul aus der Listbox eine Qualität zwischen 1 und 12 aus.
Die folgende Tabelle enthält Richtwerte zur Wahl der Genauigkeit von Schneckengetrieben nach Niemann:
| Hinweise zur Wahl der Genauigkeit von Schneckengetriebe1
| ||
| Qualität | Anwendungsgebiet | |
| Schnecke\(^a\), Rad\(^a\) und Gehäuse\(^b\) | Achsabstand\(^c\) | |
| 4 ... 5 | 6\(^d\) | Teilgetriebe für Werkzeugmaschinen, Regler, Richtgeräte (hierfür Taumelfehler besonders einschränken), Getriebe für extreme Laufruhe mit \(v_{m1} > 5 m/s\) |
| 5 ... 6 | 7\(^d\) | Aufzüge, Drehwerke, laufruhige Leistungsgetriebe mit \(v_{m1} > 5 m/s\) |
| 8 ... 9 | 8\(^d\) | Industriegetriebe ohne besondere Anforderungen an die Laufruhe, \(v_{m} < 10 m/s\) |
| Herstellung: Schnecken meist einsatzgehärtet oder randgehärtet, geschliffen, evtl.
poliert; Schneckenräder wälzgefräst und eingelaufen
| ||
| 10 ... 12 | 10\(^d\) | Nebenantriebe, Handantriebe, Stellgetriebe \(v_{m1} \le 3 m/s\) |
| \(^a\)Nach DIN 3961 bis 3963; die Profilabweichungen am Rad sind weniger kritisch; die Flanken laufen
sich ein. Teilungs-Einzel- und Summenabweichungen sowie Rundlaufabweichungen sind leicht
einzuhalten
| ||
| \(^b\)Parallelität der Achsen nach DIN 3964
| ||
| \(^c\)Nach DIN 3964
| ||
| \(^d\)Für 1- und 2-gängige Schnecken, für mehrgängige Schnecken eine Qualität feiner
| ||
| 1 Tabelle aus: Niemann, G.: Maschinenelemente, Bd. 3, Schraubrad-, Kegelrad-, Schnecken-,
Ketten-, Riemen-, Reibradgetriebe, Kupplungen, Bremsen, Freiläufe, 1986, S. 98, Tafel 25/6
| ||
Hinweis: Bei hoch belasteten Schneckengetrieben mit gehärteter und geschliffener Stahlschnecke sowie
gefrästen Schneckenrad aus einlauffähigem Werkstoff ist die Qualität der Schnecke nach Möglichkeit um
eine Stufe besser als die Qualität des Rades zu wählen. Während des Einlaufprozesses verbessert sich im
Allgemeinen die Qualität des Schneckenrades. Für die Schnecke könnte z.B. Qualität 8, für das Rad
Qualität 9 gewählt werden.
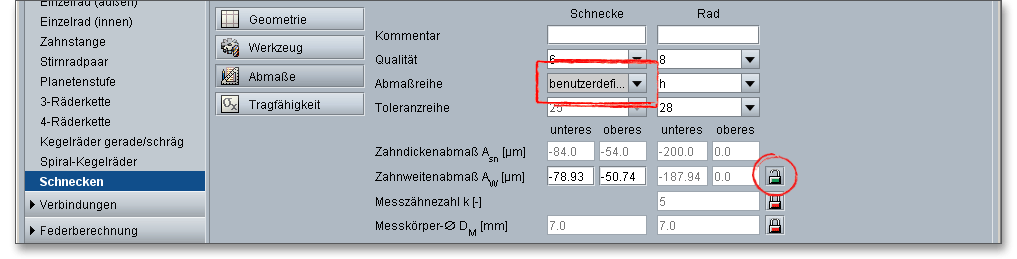
In dem DIN-Getriebe-Passsystem kennzeichnet man den Abstand des Toleranzfeldes vom Nennmaß mit einem Buchstaben, seine Breite mit einer Zahl. Bei Verzahnungen gibt es nur Spielpassungen, deshalb kommen nur die Buchstaben h bis a vor. Die Toleranzen für Schneckengetriebe sind mit DIN 3974 genormt. Das Toleranzsystem ist weitgehend an die Norm DIN 3961 für Stirnradverzahnungen angelehnt. Wählen Sie in der Listbox den Eintrag „benutzerdefiniert“, dann wird das Eingabefeld für die Zahndickenabmaße freigeschaltet und Sie haben die Möglichkeit, individuelle Daten festzulegen.
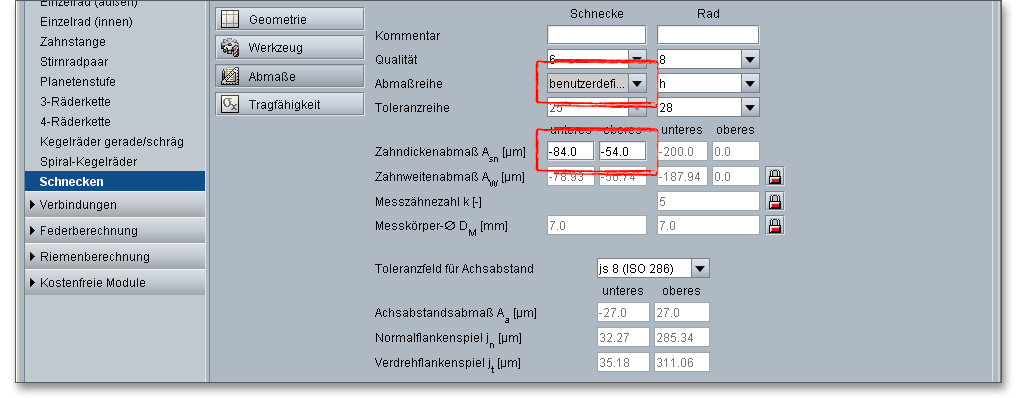
Infolge einer größeren Ausdehnung der Zahnräder als Wärmequelle gegenüber dem Gehäuse ist ohne elastische Elemente kein spielfreier Einbau möglich. Es müssen deshalb die Zahndickenabmaße so festgelegt werden, dass kein Klemmen der Zahnräder auftritt. Um dieses Klemmen der Zahnräder beim Betrieb zu vermeiden, müssen die Zähne um einen Mindestbetrag - das obere Zahndickenabmaß \(A_{sne}\) - dünner als die Nenn-Zahndicken sein. Die Verkleinerung der Zahndicken nennt man auch Zahndickenabmaß \(A_{sn}\). \(A_{sn}\) ist immer negativ.
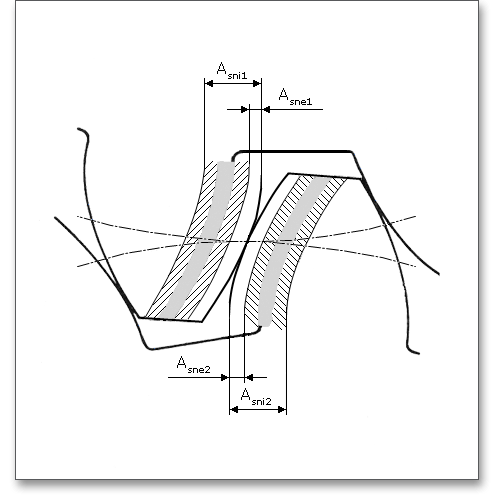
Das Zahnweitenabmaß \(A_{W}\) ist der Unterschied zwischen dem Ist- und Nennmaß der Zahnweite \(W{_k}\). Das Istmaß der Zahnweite wird bei Außenräder durch negative Abmaße kleiner als das Nennmaß für den spielfreien Eingriff. Wie auch bei dem Zahndickenabmaß gibt es hier ein oberes und ein unteres Zahnweitenabmaß, die mit \(A_{We}\) und \(A_{Wi}\) definiert sind. Bei einer eigenen Eingabe der Zahndickenabmaße können optional die Zahnweitenabmaße vorgegeben werden. Bei dieser eigenen Eingabe wird der Schloss-Button neben dem Eingabefeld für die Zahnweitenabmaße aktiviert. Diese können somit geändert werden.
Bei Schnecken wird die Dreidrahtmethode verwendet. Dieses Verfahren liefert recht genaue Ergebnisse, ist
aber auch sehr komplex. Angelehnt an Gewindemessungen hat G. Bock Berechnungsgänge entwickelt, die es
gestatten, die Dreidrahtmethode auf Getriebeschnecken aller Flankenformen anzuwenden, um somit die
Zahndicke zu bestimmen. Bei der Dreidrahtmethode werden drei gleich große kalibierte Messzylinder
(Messdrähte) in gegenüberliegende Windungen einer Schraube eingelegt. Anschließend wird die gesamte
Länge quer zur Schraubenachse über die Messzylinder, das sogenannte Prüfmaß, festgestellt. Im
eAssistant findet die Methode nach G. Bock Anwendung (Bock G., Noch R., Steiner O.: Zahndickenmessung
an Getriebeschnecken nach der Dreidrahtmethode. Physikalisch-Technische Bundesanstalt, Braunschweig,
1974).
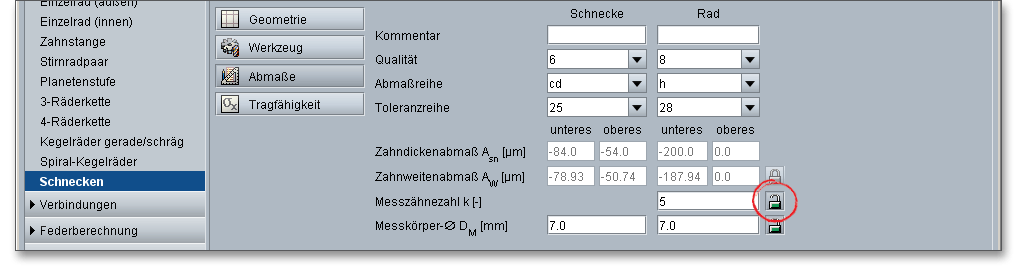
Das Berechnungsmodul gibt Ihnen die Messzähnezahl für das Schneckenrad, also die Anzahl der Zähne, über die zu messen ist, vor. Über den Schloss-Button können Sie das Eingabefeld freischalten und einen eigenen Wert für die Messzähnezahl angeben. Klicken Sie erneut auf den Button, wird der ursprüngliche Wert wieder eingesetzt. Auch für den Messkörperdurchmesser wird Ihnen automatisch ein Wert vorgegeben. Mit einem Klick lässt sich das Eingabefeld freischalten und ein eigener Wert einsetzen. Auch hier gilt: Klicken Sie erneut auf den Button, wird der usprüngliche Wert wieder eingesetzt.
Um ein Klemmen der Räder zu vermeiden, muss zwischen den Flanken stets ein Spiel vorhanden sein. Wesentliche Einflussgrößen auf das Flankenspiel sind der Achsabstand und die Passgrößen der Verzahnung. Das Getriebe-Passsystem definiert die Abweichungen des Achsabstandes mit dem Flankenspiel. In dem Passsystem der DIN wird nur ein Toleranzfeld des Achsabstandes angewendet. Beim Achsabstand werden die Abmaße für das JS-Feld angegeben. Diese entsprechen genau den ISO-Grundtoleranzen. Die Flankenspiele sind abhängig vom Zahndickenabmaß, Zahnweitenabmaß und Achsabstand. Mit der Änderung des Achsabstandes ändert sich dann auch das jeweilige Flankenspiel.
Wählen Sie in der Listbox die Option „benutzerdefiniert“, dann haben Sie die Möglichkeit, eigene Achsabstandsabmaße festzulegen. Bestätigen Sie Ihre Eingaben mit der Enter-Taste. Die Flankenspiele werden dann automatisch berechnet.

Das Achsabstandsmaß \(A_{a}\) ist die zulässige Abweichung des Achsabstandes \(a\) im Getriebe vom Nennmaß des Achsabstandes. Die Abmaße sind mit \(\pm \) angegeben, um bei Getrieben mit mehreren Achsen keine unzulässig großen Abweichungen von den Nennmaßen der Achsabstände zu erhalten.
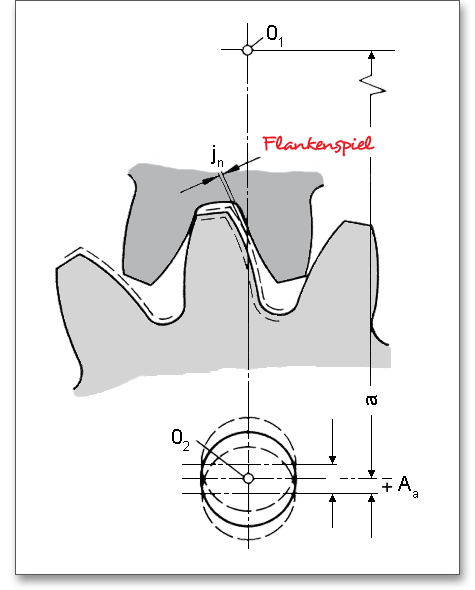
Um ein Klemmen der Zahnräder infolge der Wärmeausdehnung von Gehäuse und Radkörper zu verhindern und um Herstellungs- oder Einbauungenauigkeiten zu vermeiden, ist, wie auch bei Stirnradverzahnungen, ein Flankenspiel für Schneckengetriebe notwendig. Schneckenverzahnungen erfordern oft ein größeres Flankenspiel als Stirnräder, da die Schnecke aus Stahl und das Rad aus Schleuderbronze hergestellt und in einem Gehäuse gelagert werden. Die hohen Gleitgeschwindigkeiten verursachen erhebliche Temperaturschwankungen und die Werkstoffe dehnen sich unterschiedlich stark aus und führen so zu einer Änderung des Flankenspiels.
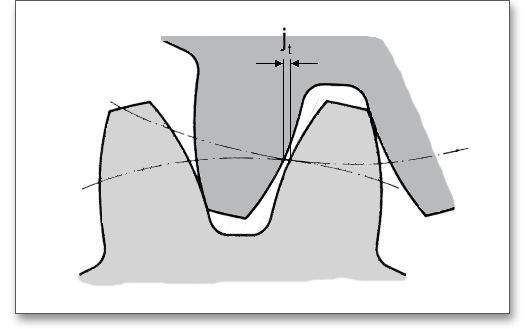
Das Verdrehflankenspiel ist die Länge des Teilkreisbogens, um den bei festgehaltener Schnecke das Schneckenrad aus der Anlage der Arbeitsflanken bis zur Anlage der Rückenflanken gedreht werden kann.
Die Tragfähigkeit von Schneckengetrieben wird weitgehend von der Werkstoffpaarung beeinflusst. Auch die Erwärmung, hervorgerufen durch die Flankenreibung, ist zu beachten. Die Berechnung der Tragfähigkeit erfolgt nach DIN 3996 Methode B, ISO/TR 14521 Methode B sowie nach Niemann. Die Berechnungen nach DIN und ISO sind recht ähnlich.
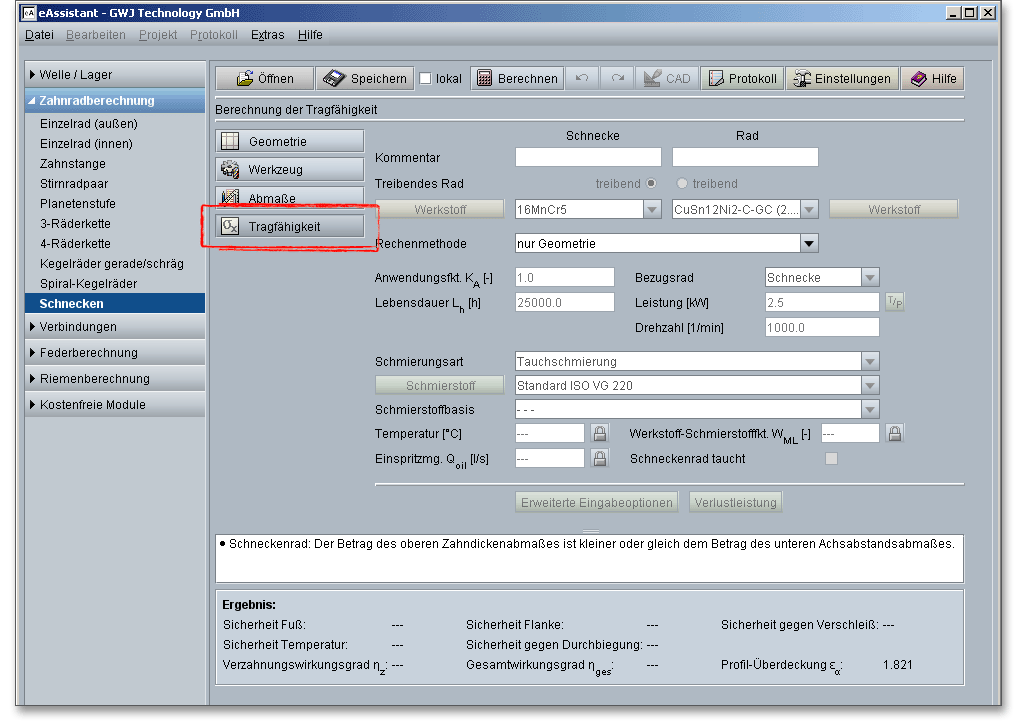
Wenn Sie auf den Button „Tragfähigkeit“ klicken, dann gelangen Sie in den Berechnungsbereich für die Tragfähigkeit. Sie werden bemerken, dass im Moment alle Eingabe- oder Auswahlfelder deaktiviert sind. Sobald Sie in der Listbox „Rechenmethode“ „DIN 3996 Methode B“, „ISO/TR 14521 Methode B“ oder „Niemann“ auswählen, werden alle Eingabefelder aktiviert. Für den Fall, dass Sie die Tragfähigkeitsberechnung nicht benötigen, kann diese somit „ausgeschaltet“ werden. Dadurch verringert sich der Umfang des Berechnungsprotokolls. Die Berechnung erfasst folgende Tragfähigkeitsgrenzen:
Die erweiterten Eingabeoptionen bieten die Möglichkeit, zusätzliche Angaben, wie zulässige Qualitätsverschlechterung oder Lagerung der Schneckenwelle, hinzuzufügen.
Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung für Schnecke und Schneckenrad. Die Bemerkung erscheint später im Protokoll im Bereich der Tragfähigkeit.
Die Auswahl der Werkstoffe für Schnecke und Schneckenrad ist besonders wichtig aufgrund des zusätzlichen Schraubengleitens der Zähne. Gute Gleiteigenschaften, Verschleißfestigkeit und gute Wärmeleitfähigkeit sind dabei gefragt. Damit sich die gleitenden Flächen schnell und ohne Fressen anpassen und auch Fertigungsabweichungen und Verformungen ausgleichen, sollte die Materialpaarung zudem ein gutes Einlaufverhalten zeigen. Daher werden Schnecke und Schneckenrad aus unterschiedlichen Werkstoffen gefertigt. Übliche Werkstoffe für Schnecken sind Einsatz- oder Nitrierstähle. Schneckenräder bestehen überwiegend aus Bronze (CuSn). Wählen Sie hier den entsprechenden Werkstoff direkt aus der Listbox oder klicken Sie auf den Button „Werkstoff“ über den Sie anschließend in die Werkstoffdatenbank gelangen.
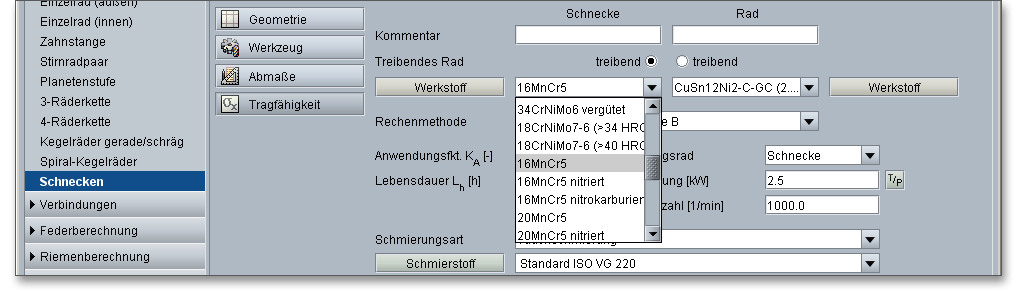
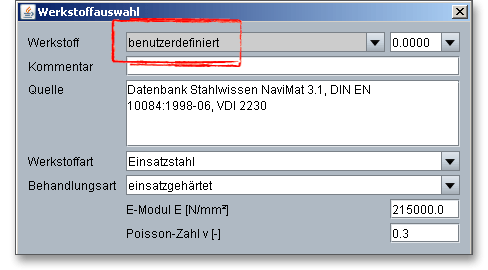
In der Werkstoffdatenbank erhalten Sie detaillierte Informationen zu den einzelnen Werkstoffen. Klicken Sie sich mit Hilfe der Cursor-Taste nach unten durch die Listbox. Somit lassen sich die einzelnen Werkstoffe anhand ihrer Eigenschaften schnell miteinander vergleichen.
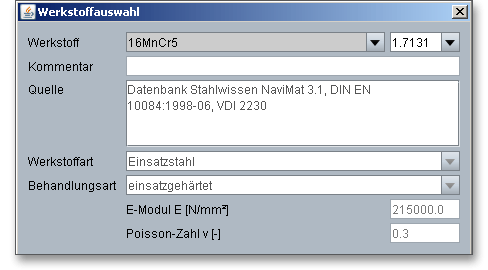
Hinweis: Wenn Sie die Option „benutzerdefiniert“ auswählen, werden alle Eingabe- und Auswahlmöglichkeiten aktiviert und Sie können Ihren individuellen Werkstoff anlegen. Ihre Eingaben werden beim Speichern in die Berechnungsdatei mitgespeichert. Wählen Sie allerdings im Modul einen anderen Werkstoff aus der Listbox aus, gehen Ihre definierten Angaben verloren. Diese müssen Sie anschließend erneut eingeben.
Die von außen auf ein Getriebe einwirkenden dynamischen Zusatzkräfte werden durch den Anwendungsfaktor \(K_{A}\) bestimmt. Diese Zusatzkräfte sind abhängig von den Eigenschaften der treibenden und der getriebenen Maschine, den Kupplungen, den Massen- sowie den Betriebsverhältnissen.
| Anwendungsfaktoren \(K_{A}\) nach DIN 3990-1: 1987-122
| ||||
| Arbeitsweise der | Arbeitsweise der getriebenen Maschine
| |||
| Antriebsmaschine | gleichmäßig | mäßige Stöße | mittlere Stöße | starke Stöße |
| (uniform) | (moderate) | (heavy) | ||
| gleichmäßig (uniform) | 1,0 | 1,25 | 1,5 | 1,75 |
| leichte Stöße | 1,1 | 1,35 | 1,6 | 1,85 |
| mäßige Stöße (moderate) | 1,25 | 1,5 | 1,75 | 2,0 |
| starke Stöße (heavy) | 1,5 | 1,75 | 2,0 | 2,25 oder höher |
| 2 Tabelle aus: DIN 3990 Teil 1, Dezember 1987, S. 55, Tab.: A1
| ||||
Die Eingaben für Leistung, Drehzahl und Drehmoment gelten für das jeweilige Bezugsrad, welches in der
Listbox ausgewählt ist. Für das andere Rad werden Drehzahl und Drehmoment aus den Eingaben für das
Bezugsrad ermittelt.
Die Leistung, das Drehmoment sowie die Drehzahl sind voneinander abhängig. Über den nebenstehenden
Button „T/P“ können Sie zwischen der Eingabe für das Drehmoment und der Eingabe für die Leistung
wechseln. Wenn Sie auf den Button „T/P“ klicken, können Sie entweder das Drehmoment oder die Leistung
eingeben bzw. umrechnen lassen. Die Bezeichnung ändert sich dann entsprechend in Drehmoment oder
Leistung.
Die Anforderungen an einen geeigneten Schmierstoff sind bei Schneckengetrieben sehr hoch. Die richtige Auswahl des Schmiermittels ist entscheidend für die Betriebssicherheit und Lebensdauer. Anforderungen an Schmierstoffe für Schneckengetriebe sind zum Beispiel:

Freiliegende Schneckengetriebe werden mit Fett geschmiert, bei geschlossenen Gehäusen kann
auch Öl zur Schmierung eingesetzt werden. Allerdings eignet sich die Fettschmierung nur für
niedrige Umfangsgeschwindigkeiten. In Abhängigkeit von der Umfangsgeschwindigkeit kommen für
Schneckengetriebe folgende Schmierungsarten zum Einsatz (Anhaltswerte nach Decker: Maschinenelemente,
S. 553):
1. Schnecke, eintauchend
2. nur Schneckenrad eintauchend

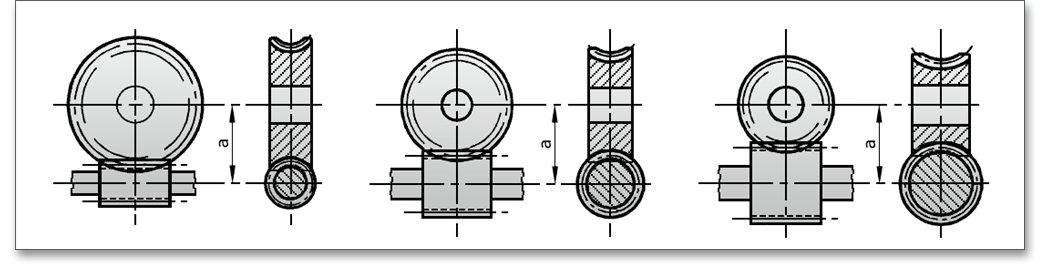
Bei einer Einspritzschmierung kann die Schnecke beliebig oben, unten oder seitlich zum Schneckenrad
angeordnet werden. Bei einer Tauchschmierung legt man die Schnecke je nach Umfangsgeschwindigkeit
möglichst nach unten. Für \(\nu _{1} \le \) 1 m/s kann sie auch seitlich, für \(\nu _{1} \le \) 5 m/s auch oben liegen.
Wenn Sie auf den Button „Schmierstoff“ klicken, gelangen Sie in die umfangreiche Schmierstoffdatenbank. Hier erhalten Sie detaillierte Informationen zu den Ölen und Fetten, wie zum Beispiel die Dichte, die Viskosität oder die Einsatztemperaturen.
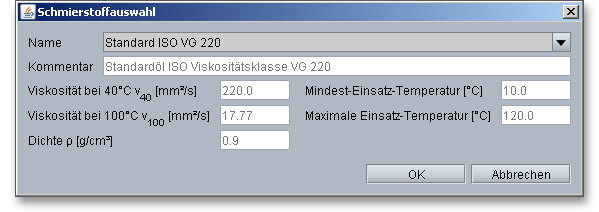
Wählen Sie aus der Listbox „benutzerdefiniert“, so lässt sich auch hier ein individueller Schmierstoff definieren.
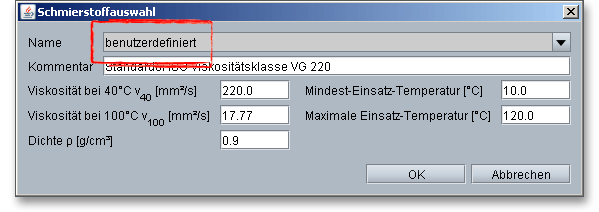
Geeignete Schmiermittel sind zum Beispiel Mineralöle mit EP-Zusätzen. Diese erleichtern den Einlauf und mindern die Fressgefahr. Auch spezielle Syntheseöle finden Anwendung. Dazu gehören Polyalphaolefin oder Polyglykol. Mit diesen Syntheseölen ist es möglich, niedrigere Reibungszahlen zu erreichen und somit den Wirkungsgrad zu steigern. Zudem werden höhere Betriebstemperaturen möglich und der Reibverschleiß wird gemindert.

Der Werkstoff-Schmierstofffaktor \(W_{ML}\) berücksichtigt den Einfluss der Kombination von Schneckenradwerkstoff und Schmierstoff auf das Verschleißverhalten. Werden andere Werkstoffe bzw. Schmierstoff als die in der folgenden Tabelle verwendet, sollten nach Möglichkeit Versuche durchgeführt werden, um die Auswirkungen abzuschätzen.
| Werkstoff-Schmierstofffaktor \(W_{ML}\)3
| ||||
| Schnecke: 16MnCr5 nach DIN EN 10084 | Werkstoff-Schmierstofffaktor \(W_{ML}\) | |||
| Schneckenradwerkstoff | Nach | Mineralöl | Polyalphaolefin | Polyglykol |
| CuSn12-C-GZ | 1,6\(^{1)}\) | 1,6\(^{1)}\) | 2,25\(^{2)}\) | |
| CuSn12Ni2-C-GZ | 1,0\(^{1)}\) | 1,0\(^{1)}\) | 1,75\(^{2)}\) | |
| CuSn12Ni2-C-GC | DIN EN 1982 | 4,1\(^{2)}\) | 4,1\(^{2)}\) | 4,1\(^{2)}\) |
| CuAl10Fe5Ni5-C-GZ | 1 | 1 | -\(^{3)}\) |
|
| EN-GJS-400-15 | DIN EN 1563 | 1\(^{1)}\) | 1\(^{1)}\) | 1\(^{1)}\) |
| EN-GJL-250 | DIN EN 1561 | 1\(^{1)}\) | 1\(^{1)}\) | 1\(^{1)}\) |
| 1) Streubereich \(\pm \) 25\(\%\)
| ||||
| 2) Streubereich \(\pm \) 30\(\%\)
| ||||
| 3) nicht betreibbar
| ||||
| 3 Tabelle aus: DIN 3996, September 2012, S. 38, Tab.: 6
| ||||
Der Wert für den Werkstoff-Schmierstofffaktor kann über den Schloss-Button individuell modifiziert werden. Aktivieren Sie dazu den Schloss-Button, um das Eingabefeld freizuschalten. Geben Sie einen Wert für den Schmierstofffaktor ein. Klicken Sie erneut auf den Button, wird der ursprüngliche Wert wieder eingesetzt.

Klicken Sie auf den Button „Erweiterte Eingabeoptionen“, um weitere zusätzliche Eingaben zu definieren. Dazu gehören zum Beispiel die zulässige Qualitätsverschlechterung, Umgebungstemperatur oder Eingaben zur Lagerung. Je nach Berechnungsmethode (DIN, ISO, Niemann) variieren die erweiterten Eingabemöglichkeiten.
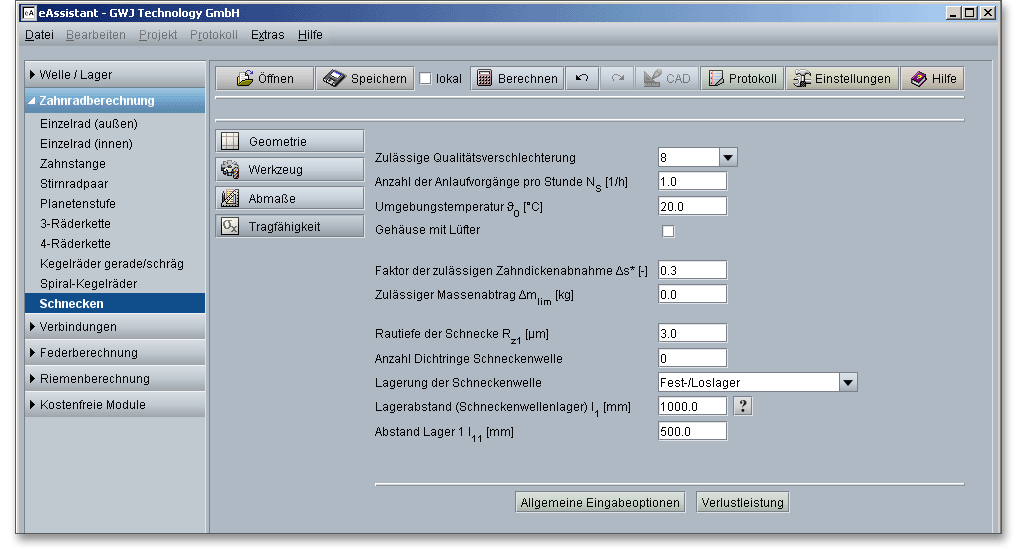
Durch zu hohe Zahnfußspannungen können die Schneckenradzähne plastisch verformt werden oder auch
ausbrechen. Die Qualität des Schneckenrades kann sich über die Zeit durch die plastischen Verformungen
und Abnutzung verschlechtern. DIN 3996 empfiehlt für Schneckenräder der Qualität besser als 7 auf die
Erfahrungen der Hersteller zurückzugreifen. Wenn eine Qualitätsverschlechterung tolerierbar ist,
dann sind nach DIN 3996 höhere Werte zulässig. Das Eingabefeld zeigt die in der Hauptmaske
„Abmaße“ eingegebene Qualität an. Die zulässige Qualitätsverschlechterung darf diesen Wert nicht
unterschreiten.
Weiter ist zwischen Getrieben mit und ohne Lüftern zu unterscheiden. Werden Lüfter eingesetzt, verändert
sich die Wärmeabgabe. Bei kleineren Getrieben liegen die Wärmedurchgangszahlen für Getriebe mit
Lüftern um etwa 30% höher als für Getriebe ohne Lüfter. Mit zunehmender Schneckendrehzahl und
zunehmendem Achsabstand verstärkt sich diese Tendenz noch. Die Wärmedurchgangszahl ist abhängig
vom Aufbau des Getriebes sowie von der Schneckendrehzahl. Steigt die Schneckendrehzahl, steigt auch
Wärmedurchgangszahl.
Die zulässige Zahndickenabnahme \(\Delta \)s am Schneckenrad ist die Abnahme der Zahnfußdickensehne durch Verschleiß im Laufe der geforderten Lebensdauer. Die Zahndickenabnahme wird benötigt, um die Verschleißsicherheit zu berechnen und findet bei der Zahnfußsicherheit Berücksichtigung.
Verschleiß entsteht durch Abtragen des Werkstoffes infolge von Gleitgeschwindigkeit, Betriebstemperatur, Art
des Schmierstoffes usw. Durch den Materialabtrag wird der Schmierstoff verunreinigt und die Schmierfähigkeit
gemindert. In Abhängigkeit von den Ölwechselintervallen, der Ölmenge oder der Lagerschmierung lässt sich
der maximal zulässige Massenabtrag \(\Delta m_{lim}\) definieren.
Niemann gibt Anhaltswerte für die gemittelte Rautiefe der Schneckenflanken:
Geschliffen \(R_{z} \le \) 3...4 \(\mu \)m für m \(\le \) 8, \(R_{z} \le \) 8 \(\mu \)m für m > 8
Gefräst \(R_{z} \le \) 12,5 \(\mu \)m für m \(\le \) 8, \(R_{z} \le \) 25 \(\mu \)m für m > 8
Die Dichtringe verhindern das Austreten von Öl und bieten Schutz gegen das Eindringen von
Verunreinigungen. Die Anzahl der Dichtringe kann hier eingegeben werden. Diese wird für die Berechnung der
Dichtungsverlustleistung gebraucht. Die Dichtungsverlustleistung am Schneckenrad kann wegen der niedrigen
Drehzahl vernachlässigt werden.
Bei kleinen bzw. mittleren Abmessungen kommt meist eine angestellte Lagerung zum Einsatz (z.B. Schulter-
oder Schrägkugellager bzw. Kegelrollenlager). Bei größeren Kräften oder Abmessungen zieht man eine
Fest-Los-Lagerung vor (z.B. zweireihiges Schrägkugellager).
Für die Schneckenwelle sollte möglichst ein kleiner Lagerabstand definiert werden, um die Durchbiegung unter Last klein zu halten.
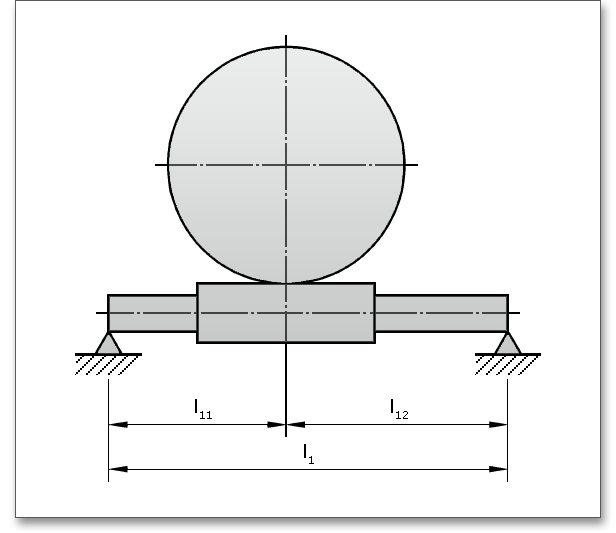
Ein Klick auf den Button „Verlustleistung“ zeigt die Verlustleistung direkt in der Software an. Bei Bedarf kann die Verlustleistung über den Schloss-Button individuell vorgeben werden. Somit kann die Tragfähigkeitsberechnung besser an Ergebnisse von Prüfstandsversuchen angepasst werden.
Das Berechnungsmodul enthält ein Meldungsfenster, in denen Informationen, Hinweise oder Warnungen aufgelistet werden. Die eAssistant-Software erkennt bereits während der Dateneingabe auftretende Fehler und zeigt Ihnen sogleich Lösungsvorschläge im Meldungsfenster an. Wenn Sie die verschiedenen Hinweise und Warnungen beachten und befolgen, lassen sich schnell Fehler in Ihrer Berechnung beheben.

Bewegen Sie den Mauszeiger über ein Eingabefeld oder über einen Button, so erhalten Sie zusätzliche Informationen, die Ihnen in der Kurzhilfe angezeigt werden.
Die Ergebnisse (Sicherheiten für Fuß, Flanke, Temperatur, Profilüberdeckung usw.) werden bereits während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld angezeigt. Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Dadurch werden jegliche Veränderungen der Eingabewerte auf die Ergebnisse schnell sichtbar. Werden die Mindestsicherheiten nicht erfüllt, so wird das Ergebnis mit einer roten Markierung angezeigt. Grundsätzlich können Sie jede Eingabe mit der Enter-Taste oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können Sie mit der Tab-Taste durch die Eingabemaske springen oder nach jeder Eingabe auf den Button „Berechnen“ klicken. Auch hierbei werden die Werte entsprechend übernommen und die Ergebnisse sofort in der Übersicht angezeigt.

Nach Abschluss Ihrer Berechnungen haben Sie die Möglichkeit, ein Protokoll zu generieren. Klicken Sie dazu auf den Button „Protokoll“, um das Protokoll zu öffnen.

Das Protokoll enthält ein Inhaltsverzeichnis. Hierüber lassen sich die gewünschten Ergebnisse schnell aufrufen. Es werden Ihnen alle Eingaben sowie Ergebnisse aufgeführt. Das Protokoll steht Ihnen im HTML- und im PDF-Format zur Verfügung. Sie können das erzeugte Protokoll zum Beispiel im HTML-Format abspeichern, um es später in einem Web-Browser wieder oder im Word für Windows zu öffnen.
Das Berechnungsprotokoll lässt sich drucken oder auch speichern:
Um das Protokoll zu speichern, rufen Sie das Menü „Datei“ auf und klicken Sie anschließend auf „Speichern unter“.
Nach der Durchführung Ihrer Berechnung können Sie diese speichern. Sie haben dabei die Möglichkeit, entweder auf dem eAssistant-Server oder auf Ihrem Rechner zu speichern. Klicken Sie auf den Button „Speichern“ in der obersten Zeile des Berechnungsmoduls.

Um die Berechnung lokal auf Ihrem Rechner zu speichern, müssen Sie die Option „Lokal“ im Berechnungsmodul aktivieren.
Haben Sie diese Option nicht aktiviert, so öffnet sich ein neues Fenster und Sie können Ihre Berechnung auf dem eAssistant-Server speichern. Geben Sie unter „Dateiname“ den Namen Ihrer Berechnung ein und klicken Sie auf den Button „Speichern“.
Mit dem Button „Zurück“ (linker Pfeil) können Sie vorhergegangene Eingaben zurücksetzen. Wenn Sie eine rückgängiggemachte Eingabe wiederherstellen wollen, dann klicken Sie auf den Button „Vorwärts“ (rechter Pfeil).

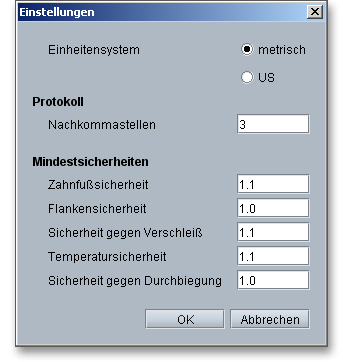
Klicken Sie auf den Button „Einstellungen“ in der obersten Zeile des Berechnungsmoduls.

Diese Option gibt Ihnen die Möglichkeit, die folgenden Standardeinstellungen im Berechnungsmodul zu ändern: