[Nächstes Kapitel] [vorangehendes Kapitel] [vorangehendes Kapitel (SeitenEnde)] [SeitenEnde] [Inhalt]
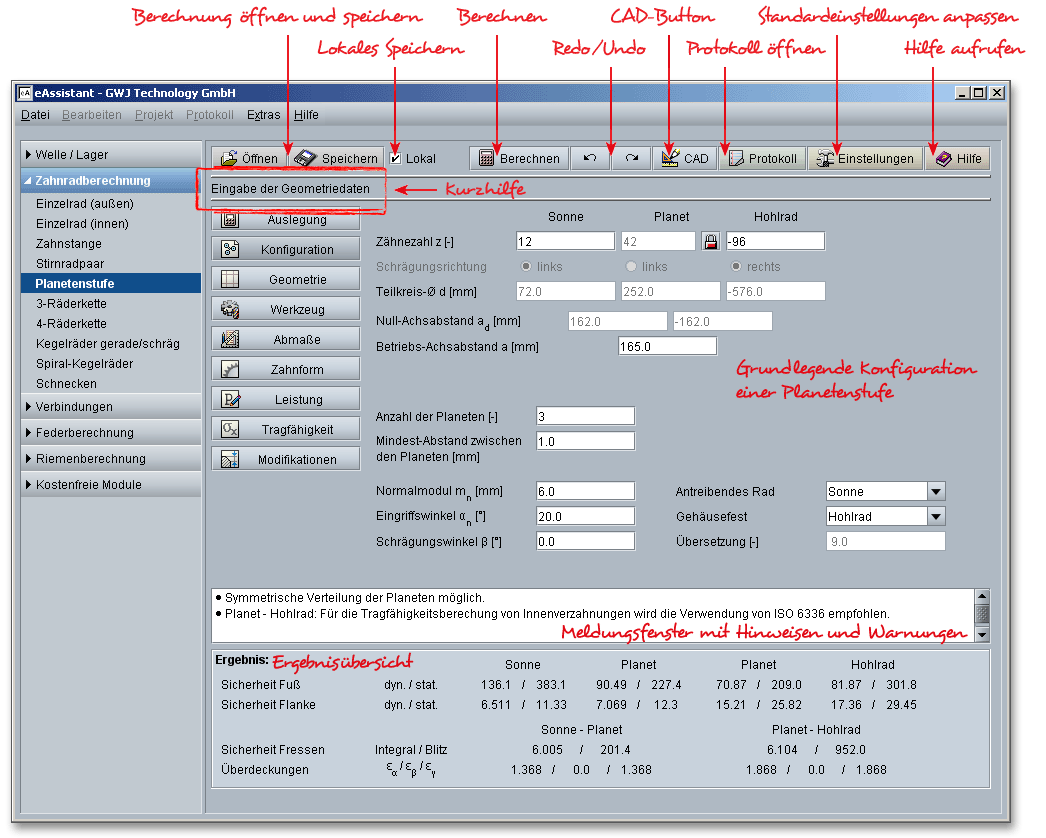
Melden Sie sich auf der Startseite www.eAssistant.eu mit Ihrem Benutzernamen und Ihrem Passwort an. Um das Berechnungsmodul für Planeten zu starten, klicken Sie in der Baumstruktur auf der linken Seite auf den Menüpunkt „Zahnradberechnung“ und anschließend auf „Planetenstufe“.

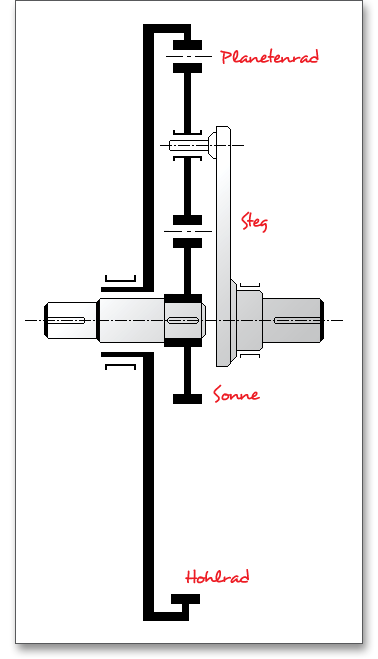
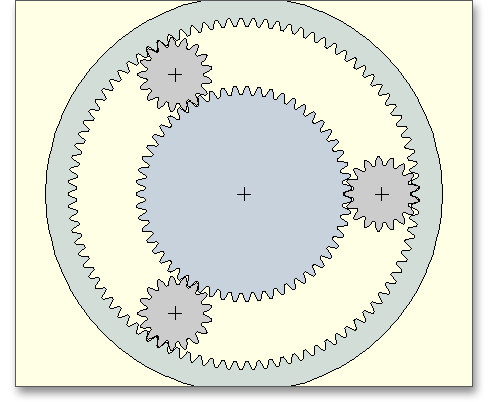
Das Planetengetriebe ist eine Sonderbauart des Stirnradgetriebes. Bei den Planetengetrieben, oft auch als
Umlaufgetriebe- oder Umlaufrädergetriebe bezeichnet, lassen sich zwei verschiedene Arten unterscheiden -
einfache und zusammengesetzte Planetengetriebe. Das eAssistant-Modul berechnet die einfache Bauform
eines Planetengetriebes. Dieses besteht aus einem außenverzahnten Sonnenrad, den von dem
Planetenträger (Steg) getragenen Planetenrädern und einem innenverzahnten Stirnrad (Hohlrad). Die
Zahnkräfte verteilen sich gleichmäßig auf mehrere Planeten und sind dadurch relativ gering.
Durch den einfachen Aufbau des Getriebes und der günstigen Eigenschaften ergeben sich viele
Einsatzmöglichkeiten. Deshalb ist es auch eine der bekanntesten und am häufigsten verwendete Bauart für
Industriegetriebe.
Vorteile von Planetengetrieben:
Nachteile von Planetengetrieben
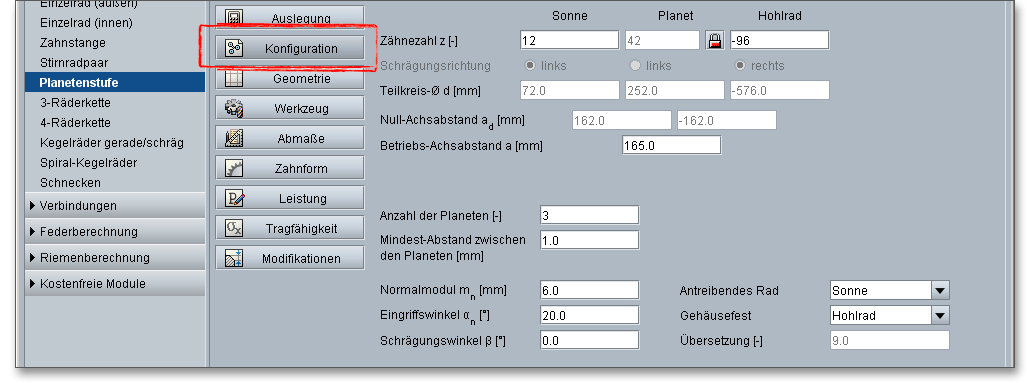
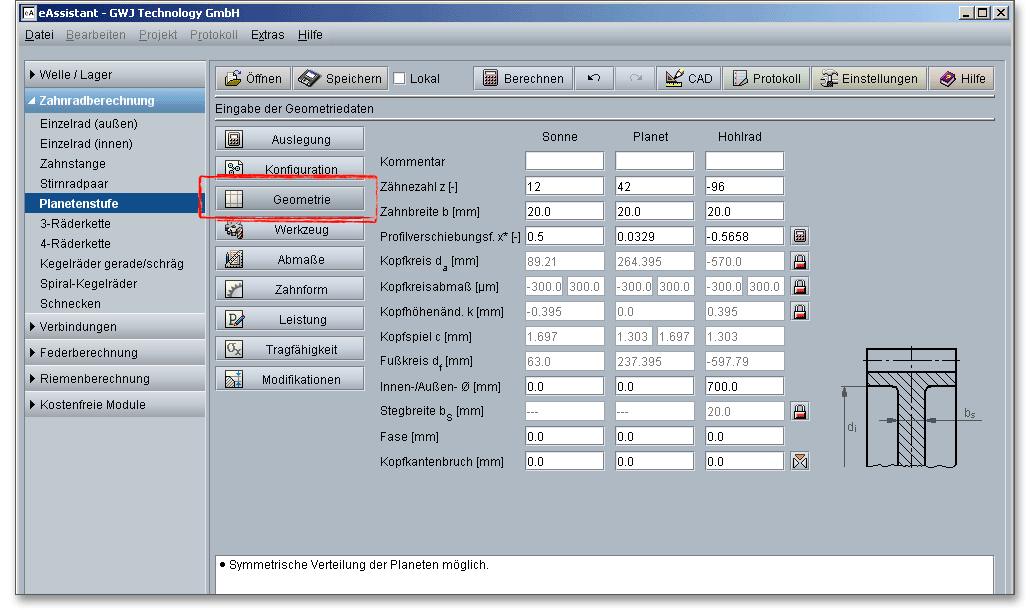
Die grundlegende Konfiguration startet mit der Eingabe der Zähnezahlen für Sonne, Planet und Hohlrad. Das Sonnenrad sowie die Planeten sind außenverzahnt und sind deshalb positiv definiert. Für die Zähnezahl des Hohlrades ist ein negatives Vorzeichen einzusetzen. In der Hilfe zum Stirnrad erhalten Sie eine Übersicht mit Richtwerten zur Wahl der Mindestzähnezahl und Zahnbreite. Die Zähnezahlen von der Sonne und dem Hohlrad sind gewöhnlich durch die Übersetzung und den Modul festgegelegt. Die Zähnezahl des dazwischen liegenden Planetenrades hat dagegen keinen Einfluss auf die Übersetzung und somit auf die Getriebeeigenschaft.
Hinweis: Die Ergebnisse werden bereits während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld
angezeigt. Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Grundsätzlich können Sie jede
Eingabe mit der Enter-Taste oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können
Sie mit der Tab-Taste durch die Eingabemaske springen oder nach jeder Eingabe auf den Button
„Berechnen“ klicken. Auch hierbei werden die Eingabewerte entsprechend übernommen und die Ergebnisse
sofort in der Übersicht angezeigt. Wenn Sie die Konfiguration des Planetengetriebs festlegen,
können Sie sich die dazugehörige Zahnform jederzeit über den Button „Zahnform“ ansehen.
Klicken Sie auf „Geometrie“ oder „Werkzeug“, dann gelangen Sie wieder in die entsprechenden
Hauptmasken.
Sobald Sie einen Schrägungswinkel eingeben, lässt sich über die Radiobuttons die Schrägungsrichtung festlegen. Bei einer Außenverzahnung kämmt ein rechtssteigendes Rad mit einem linkssteigenden Gegenrad, bei Innenradpaaren müssen die Flankenrichtungen übereinstimmen.

Wählen Sie bei der Sonne die Schrägungsrichtung „links“ aus, dann ist die Sonne linkssteigend, das Planetenrad rechtssteigend, das Hohlrad rechtssteigend.

Wählen Sie beim Planetenrad die Schrägungsrichtung „links“ aus, dann ist die Sonne rechtsteigend, das Planetenrad linkssteigend, das Hohlrad linksstiegend.

Hinweis: Die Schrägungsrichtung des Hohlrades kann nicht direkt vorgegeben werden. Sie ergibt sich
automatisch aus der vorgegebenen Schrägungsrichtung der Sonne oder des Planeten.
Die Teilkreisdurchmesser werden jeweils für Sonne, Planet und Hohlrad automatisch berechnet. Der
Teilkreisdurchmesser ist für die Baugröße des Planetengetriebes bestimmend. Mit der Anzeige haben Sie
jederzeit die Baugröße im Blick und können gegebenenfalls die Größe über das Eingabefeld für den Modul
oder die jeweilige Zähnezahl ändern.
Der Null-Achsabstand ist eine reine Rechengröße und ergibt sich aus der Summe der Teilkreisradien. Aus dem
Modul und den Zähnezahlen errechnen sich die Achsabstände automatisch. Die Nullachsabstände \(a_{d}\) für die
Paarungen Sonne-Planet und Planet-Hohlrad werden angezeigt. Der Betriebsachsabstand \(a\) wird zwar
automatisch bestimmt, kann jedoch auch manuell angepasst werden. Dadurch ergibt sich so eine einfache
Möglichkeit, den Achsabstand beliebig zu modifizieren. Bei einer Innenradpaarung ist der Achsabstand stets
negativ, deshalb erhält der Wert für die Paarung Planet-Hohlrad ein negatives Vorzeichen. \(a_{d}\) entspricht dem
wirklichen Abstand \(a\), wenn die Summe der Profilverschiebungsfaktoren gleich Null ist. Sind also der
Null-Achsabstand und der Betriebs-Achsabstand gleich, so werden die Profilverschiebungsfaktoren automatisch
auf den Wert „0“ gesetzt.
Hinweis: Damit eine gültige Konfiguration berechnet werden kann, sollten die Null-Achsabstände der beiden
Paarungen Sonne-Planet und Planet-Hohlrad betragsmäßig etwa gleich groß sein bzw. sich nicht zu stark
unterscheiden. Es besteht auch die Möglichkeit, die Profilverschiebungsfaktoren bzw. deren Summe
vorzugeben und daraus den Achsabstand berechnen zu lassen.
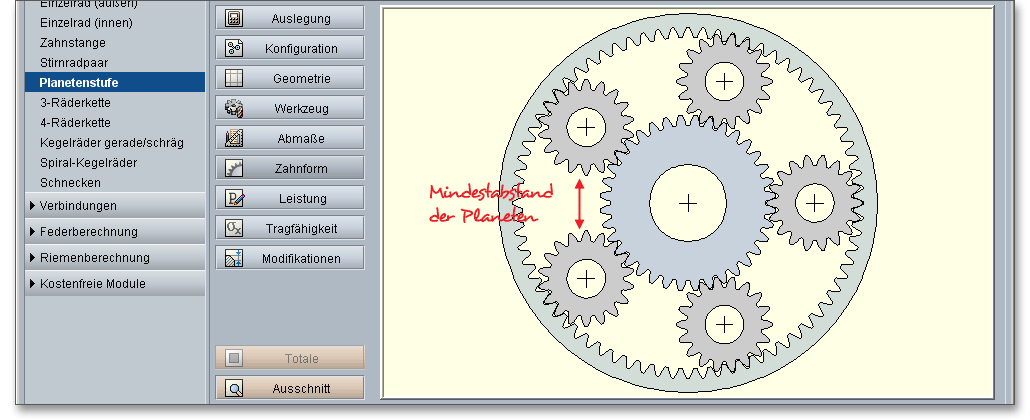
Bei einem Planetengetriebe können mehrere Planetenräder angeordnet werden. Dies hat den Vorteil, dass sich die Zahnkräfte auch auf mehrere Planetenräder verteilen, wodurch wieder ein kleinerer Modul gewählt werden kann. Die Anzahl der Planetenräder führt zu einer Leistungsverzweigung. Diese Leistungsverzweigung sowie die Innenverzahnung bewirken, dass die mechanische Belastbarkeit eines Getriebes gesteigert bzw. das Getriebe kleiner und kompakter gebaut werden kann. Die eAssistant-Software erlaubt eine beliebige Anzahl an Planetenräder. Wird die Anzahl von Planetenräder, die für die Konfiguration möglich sind überschritten, so wird dies im Meldungsfenster angezeigt. Die Berechnung des Getriebes ist dann nicht mehr durchführbar.

Geben Sie einen Mindestabstand zwischen den Planetenrädern ein. Die Einhaltung dieses vorgegebenen Mindestabstandes wird vom eAssistant überprüft. Kann der Mindestabstand nicht eingehalten werden, erhalten Sie im Meldungsfenster einen Hinweis. Die Planetenräder eines Getriebes sollen sich gleichmäßig über den Umfang verteilen. Die eAssistant-Software kontrolliert, ob die symmetrische Anordnung der Planetenrädern möglich ist und ob sich das Getriebe so montieren lässt. Ist keine symmetrische Montage möglich, werden Sie mit einem Hinweis im Meldungsfenster darüber informiert. Dabei wird die notwendige Winkelaufteilung der Planeten angegeben.
Der Normalmodul \(m_{n}\) ist eine Grundgröße der Verzahnungsgeometrie. Der Modul bestimmt die Größe der Verzahnung. Das bedeutet, dass sich mit dem Modul proportional alle Verzahnungsabmessungen vergrößern. Der Modul ist für Sonne, Planetenrad und Hohlrad gleich. Der Modul definiert sich als Quotient aus Teilkreisdurchmesser \(d\) und Zähnezahl \(z\) und wird in \(mm\) angegeben. Um die Vielfalt der Verzahnungen einzuschränken, wurde der Modul genormt (im Kapitel 8.2.1 „Normalmodul“ finden Sie die Tabellen mit den genormten Modulreihen). Die Berechnung im eAssistant ist mit beliebigen Modulen, auch mit mehreren Nachkommastellen, möglich.
Erfahrungsgemäß hat sich ein Eingriffswinkel \(\alpha _{n}\) (am Teilkreis) von \(20^{\circ }\) als günstig erwiesen. Öffnen Sie das Berechnungsmodul, ist standardmäßig ein Eingriffswinkel von \(20{^\circ }\) eingestellt. Dieser kann allerdings auch für Sonderfälle abweichend von den \(20{^\circ }\) individuell vorgegeben werden.
Mit Hilfe der Listbox lässt sich der Bewegungszustand des Planetengetriebes festgelegen. Wählen Sie den Eintrag „Planetenträger“, dann wird der Steg des Getriebes festgehalten und aus dem Planetengetriebe entsteht ein Standgetriebe.
Bei einer Schrägverzahnung sind die Zähne gegenüber der Achsrichtung um den Winkel \(\beta \) geneigt. Bei einer Geradverzahnung beträgt \(\beta \) = \(0^{\circ }\), bei Schrägverzahnungen kann \(\beta \) bis zu \(45^{\circ }\) betragen. \(45^{\circ }\) ist der Maximalwert, der in das Eingabefeld für den Schrägungswinkel eingetragen werden kann.
Die Übersetzung beschreibt das Verhältnis der Zähnezahlen der in einem Planetengetriebe vorkommenden
Zahnräder. Das Übersetzungsverhältnis wird mit \(i\) (innere Übersetzung) bezeichnet. Ist zum
Beispiel eine Abweichung von einer bereits vorgegebenen Übersetzung zu groß, lässt sich also eine
Anpassung durch geringe Änderungen der Zähnezahlen ohne wesentliche Vergrößerung des
Getriebes erreichen. Die Übersetzung einer Planetenstufe hängt zusätzlich vom Bewegungszustand
ab.
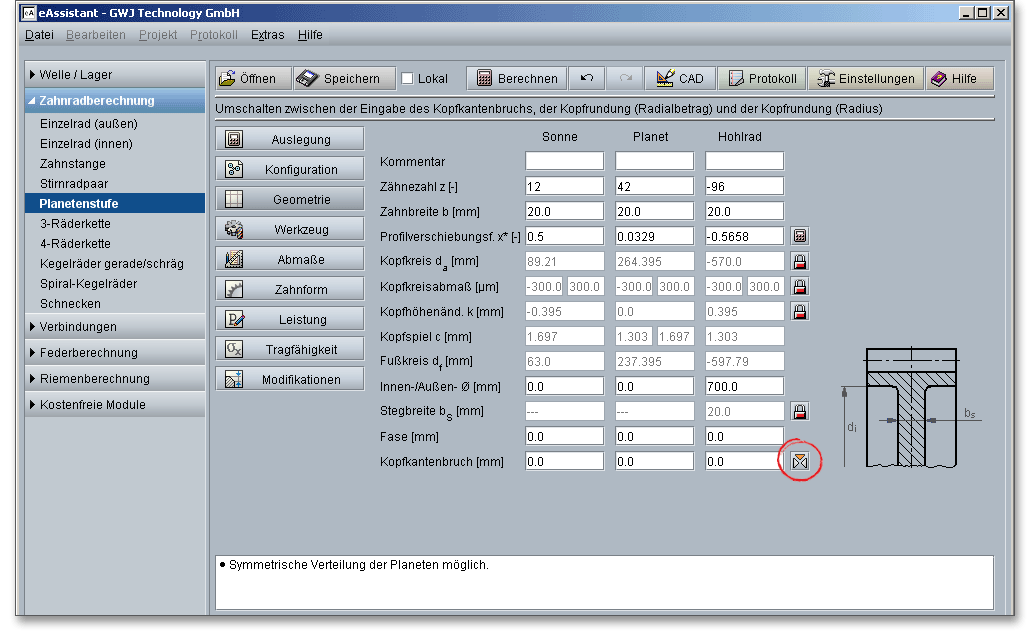
Nach dem Start der grundlegenden Konfiguration der Planetenstufe folgt nun die Eingabe der Geometriedaten. Die Berechnung der Geometrie erfolgt nach den entsprechenden DIN-Normen, wobei sich die areisdurchmesser, die Kopfkreisabmaße sowie die Kopfhöhenänderung auch manuell über den Schloss-Button beeinflussen lassen. Es besteht weiterhin die Möglichkeit, die Profilverschiebung sowie einen Kopfkantenbruch zu ergänzen, die dann anschließend auch mit in die Berechnung einfließen.
Die Zahnbreite \(b\) ist der Abstand der beiden Stirnflächen auf der Bezugsfläche einer Verzahnung. Die
Zahnbreite kann jeweils für Sonne, Planet und Hohlrad eingegeben werden.
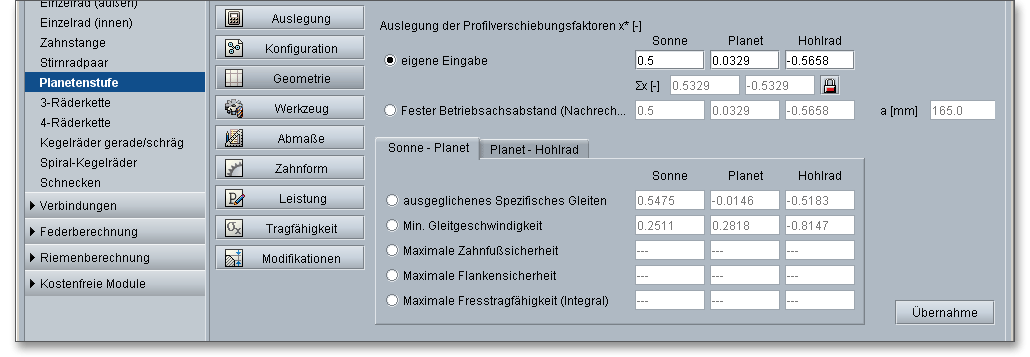
Mit Hilfe der Profiverschiebung lässt sich die Zahnform so verändern, um damit die Eigenschaften des Zahnrades zu beeinflussen. Die Profilverschiebung wird auf Sonne, Planet und Hohlrad aufgeteilt. Man unterscheidet, je nach Richtung der Verschiebung, eine positive und eine negative Profilverschiebung. Bei einer positiven Profilverschiebung wird das Werkzeug in Richtung Kopfkreis verschoben, bei einer negativen in Richtung Fußkreis.
Bei einer Außenverzahnung (Sonnenrad und Planetenrad) verschiebt sich der genutzte Teil der Evolvente nach außen, bei einer Innenverzahnung (Hohlrad) nach innen. Da eine positive Profilverschiebung die Tragfähigkeit bei Außenverzahnungen recht vorteilhaft beeinflusst, werden Außenverzahnungen meist auch mit einer positiven Profilverschiebung ausgelegt. Innenverzahnungen dagegen erhalten überwiegend eine negative Profilverschiebung, da sich die positive doch eher ungünstig auf die Tragfähigkeit auswirkt. Um den Profilverschiebungsfaktor einfach zu optimieren, klicken Sie auf das Taschenrechner-Symbol.

Im Berechnungsmodul gibt es mehrere Möglichkeiten, um die Profilverschiebung zu optimieren.
Geben Sie entweder Ihre eigenen Werte für die Profilverschiebungsfaktoren vor oder legen Sie die
Profilverschiebungssumme fest, um daraus den Achsabstand berechnen zu lassen. Aktivieren Sie für eine
optimale Auslegung das „ausgeglichene spezifische Gleiten“ für die beiden Paarungen Sonne-Planet oder
Planet-Hohlrad. Das ausgeglichene spezifische Gleiten ist nur für eine Paarung möglich. Die Faktoren
werden dann so angepasst, dass das spezifische Gleiten ausgeglichen ist und sich dadurch die
Verschleißerscheinungen verringern. Auf die Tragfähigkeit und geräuscharmen Lauf hat das spezifische
Gleiten positive Auswirkungen. Bei kleinen Zähnezahlen ist der Einfluss der Profilverschiebung sehr
groß, bei großen Zähnezahlen dagegen eher sehr klein. Wenn die Werte für das spezifische
Gleiten rot markiert sind, dann ist eine Auslegung nicht möglich. Die Profilverschiebungsfaktoren
werden dann anhand der Profilverschiebungssumme zu gleichen Teilen auf Planet und Hohlrad
aufgeteilt.
Außerdem gibt es die Funktion „Fester Betriebsachsabstand (Nachrechnung)“ für die Entkopplung der
Profilverschiebungssumme und des Achsabstands. Mit dieser Funktion sind die Profilverschiebungsfaktoren
unabhängig zum Achsabstand vorgebbar. Dies ermöglicht beispielsweise die Berechnung von
vorhandenen Stirnradpaaren, die mit „falschem“ Achsabstand im Gehäuse verbaut werden sollen.
Profilüberdeckung, Flankenspiel und Tragfähigkeit werden dabei korrekt mit berechnet. Weiterhin
kann diese Funktionalität auch bei der Auslegung von kleinmoduligen Verzahnungen zum Einsatz
kommen.
Weitere Optionen für die Aufteilung der Profilverschiebungsfaktoren für die Paarungen Sonne-Planet bzw. Planet-Hohlrad: „Minimale Gleitgeschwindigkeit“, „Maximale Zahnfußsicherheit“, „Maximale Flankensicherheit“ und „Maximale Fresstragfähigkeit (Integral)“. Die letzten drei Optionen stehen nur bei aktivierter Tragfähigkeit zur Auswahl.
Bei den Planetenstufen ist es ratsam, unabhängig von der Innenverzahnung (Hohlrad), eine optimale
Außenverzahnung (Sonne-Planet) nach den gängigen Methoden der Profilverschiebung festzulegen. Dabei ist
zu beachten, dass keine Eingriffsstörungen auftreten. Bei einer extrem großen Profilverschiebung treten
Eingriffsstörungen bei Außenverzahnungen vorallem am Zahnfuß des Ritzels auf. Sollten Eingriffsstörungen
vorliegen, erhalten Sie einen entsprechenden Hinweis im Meldungsfenster. In den Kapiteln 8.2.9 und 8.10.5 für
Stirnräder finden Sie weitere Informationen rund um das Thema Profilverschiebung bei Außen- und
Innenverzahnungen.
Der Kopfkreisdurchmesser \(d_{a}\) ist von dem Modul abhängig und wird so automatisch vom Programm berechnet. Ändern Sie die Profilverschiebung, dann ändert sich auch der Kopfkreis. Nun besteht die Möglichkeit, diesen Kopfkreisdurchmesser mit Hilfe des Schloss-Buttons freizuschalten, um somit den Kopfkreisdurchmesser leicht zu beeinflussen. Beachten Sie, dass der Kopfkreisdurchmesser zusätzlich auch die Kopfhöhenänderung beeinflusst. Klicken Sie erneut auf den Button, wird das Eingabefeld wieder deaktiviert und der nach DIN berechnete Wert eingesetzt.

Das Kopfkreisabmaß wird automatisch nach DIN ermittelt. Auch hier ist es möglich, das Schloss-Symbol zu aktivieren, um die Eingabefelder freizuschalten und die Werte manuell zu modifizieren. Klicken Sie wieder auf den Schloss-Button, so wird der nach DIN ermittelte Eingabewert wieder eingesetzt.

Die Kopfhöhenänderung \(k\) wird automatisch vom Programm so gesetzt, dass genügend Kopfspiel vorhanden ist. Bei Außenverzahnungen ist der Kopfhöhenänderungsfaktor \(k \le 0\), bei Innenverzahnungen setzt man häufig \(k = 0\), um Eingriffsstörungen zu vermeiden. Klicken Sie auf das Schloss-Symbol, so können Sie die Eingabefelder manuell freischalten und Ihre eigenen Werte eingeben. Durch eine Kopfhöhenänderung beeinflussen Sie den Kopfkreis und das Kopfspiel.

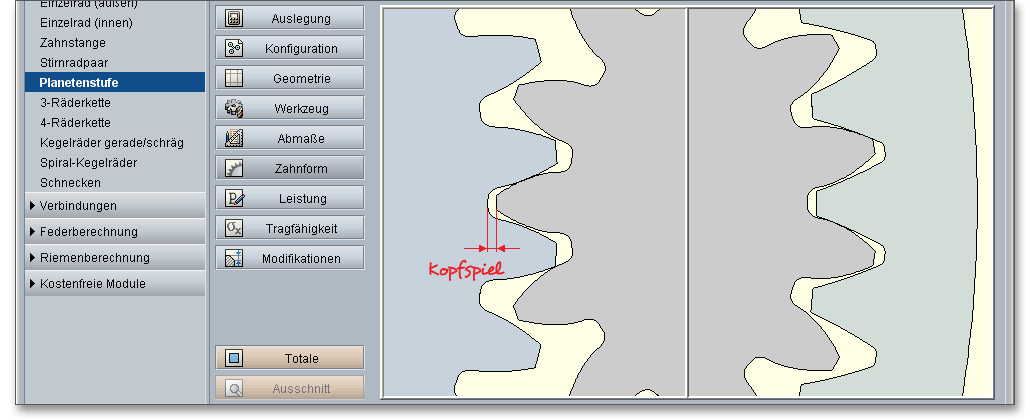
Damit eine ungestörte Bewegung zwischen den Flanken möglich wird, sind zwischen den jeweiligen Verzahnungen bestimmte Spiele notwendig. Den Abstand zwischen Kopfkreis des Rades und Fußkreis des Gegenrades nennt man Kopfspiel \(c\). Das Kopfspiel soll verhindern, dass sich Kopfkreisdurchmesser und Zahnfuß des Gegenrades berühren.
Der Fußkreisdurchmesser \(d_{f}\) ist eine Größe, die von dem jeweiligen Modul, der Profilverschiebung und der
Kopfhöhe des Werkzeug-Bezugsprofils abhängig ist und somit vom Programm berechnet wird. Der
Fußkreisdurchmesser ergibt sich also aus der Berechnung.
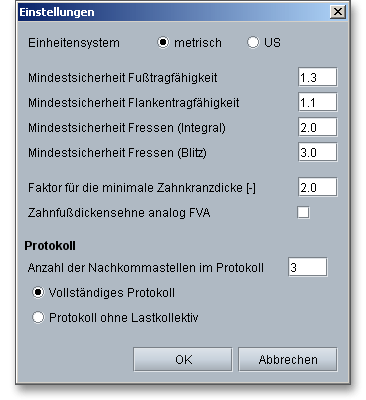
Hier haben Sie die Möglichkeit, einen Innendurchmesser (bei Sonne und Planet) bzw. Außendurchmesser (beim Hohlrad) anzugeben. Bitte beachten Sie auch die Hinweise zur Zahnkranzdicke unter 9.21 „Einstellungen“.
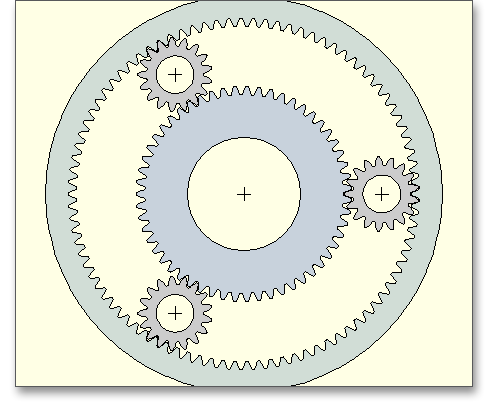
Die Breite eines Steges kann hier berücksichtigt werden. Zur Orientierung finden Sie neben den Eingabefeldern eine graphische Darstellung. Es besteht die Möglichkeit, die Stegbreite über den Schloss-Button zu beeinflussen.

Definieren Sie eine Bohrung (Innendurchmesser für Sonne und Planet). Die Stegbreite wird zunächst auf den gleichen Wert wie die Radbreite gesetzt. Ist die Stegbreite kleiner als die Radbreite, wird die Radkörpersteifigkeit beeinflusst, die über den Radkörperfaktor \(C_{R}\) mit in die Berechnung einfließt. Daraus ergeben sich veränderte Zahnfedersteifigkeiten, welche wiederum Auswirkungen auf die Tragfähigkeit haben. Über den Schloss-Button lässt sich die Stegbreite nun auch manuell modifizieren.

Eine Fase und ein Kopfkantenbruch werden in der Berechnung mit berücksichtigt. Ein Kopfkantenbruch ist eine zu gleichen Teilen auf Kopffläche und Kopfflanke verteilte Schutzfase entlang der Kopfkanten. Die Kopfkanten eines Zahnrades werden abgerundet oder mit einem Kantenbruch versehen, der vom Verzahnungswerkzeug erzeugt werden kann. Der Kopfkantenbruch bietet sich an, um z.B. Eingriffsstörungen zu beheben. Die Fase reduziert die rechnerische Zahnbreite bei der Tragfähigkeitsberechnung von Zahnfuß und -flanke. Alternativ zum Kopfkantenbruch kann eine Kopfabrundung vorgegeben werden. Diese kann entweder analog dem Kopfkantenbruch als Radialbetrag oder direkt als Radius definiert werden.
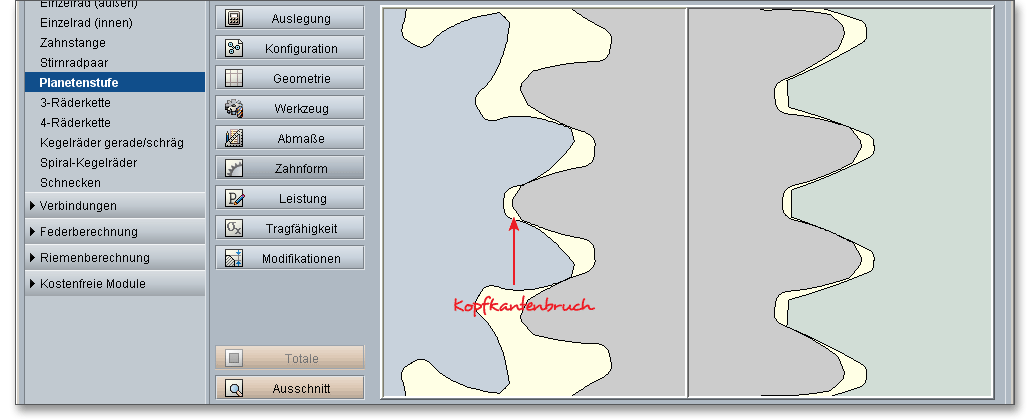
Die entsprechende Auswahl ist durch den farbigen Pfeil gekennzeichnet. Beim Kopfradius wird direkt der Radius eingegeben, beim Kopfradius (Rad.) wird der Radialbetrag eingetragen. Geben Sie den Kopfradius direkt als Wert ein, dann erhalten Sie im Berechnungsprotokoll den dazugehörigen Radialbetrag.
Bei Kopfkantenrundung oder Kopfkantenbruch ist der Kopf-Formkreisdurchmesser um den doppelten Radialbetrag \(h_{K}\) kleiner als der Kopfkreisdurchmesser.
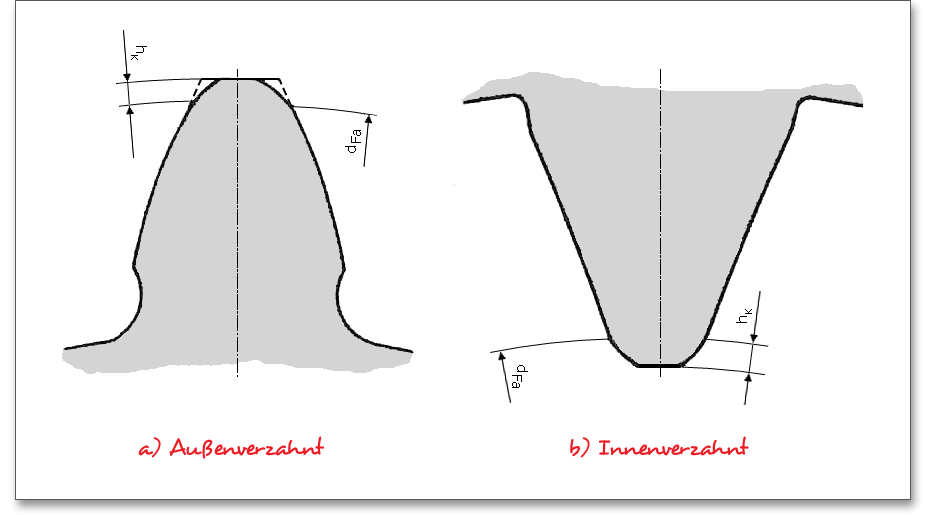
Hier können Sie aus einer Liste die Werkzeugart für Sonne, Planet und Hohlrad sowie ein vordefiniertes Werkzeugbezugsprofil nach ISO 53, DIN 867 und DIN 3972 wählen. Das Bezugsprofil lässt sich aber auch individuell vorgeben. Außerdem kann eine Bearbeitungszugabe berücksichtigt werden.
Klicken Sie auf den jeweils aktiven Pfeil, um zwischen den Stirnradpaarungen Sonne-Planet oder Planet-Hohlrad schnell hin und her zu wechseln.

Hinweis: Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung für Sonne, Planet und
Hohlrad. Die Bemerkung erscheint dann später auch im Protokoll.
Über die Listbox können Sie die Werkzeuge „Wälzfräser“ oder „Schneidrad“ für die Berechnung der Zahnform auswählen. In der Listbox steht Ihnen auch die „konstruierte Evolvente“ zur Verfügung. Die Wahl des Werkzeugs richtet sich nach der Radart (Außen- oder Innenräder). Außenverzahnungen werden spanend meist mit einem Wälzfräser hergestellt. Für das Hohlrad als Innenverzahnung nutzt man üblicherweise das Schneidrad.

Das Wälzfräsen ist das am häufigsten angewendete Verfahren für die Verzahnungsvor- und
fertigbearbeitung von Außenverzahnungen. Eine hohe Flexibilität und Produktivität sind die Vorteile des
Wälzfräsens. Beim Fräsen ist die Achse des Wälzfräsers geneigt, so dass die Schraubengänge in
Richtung der Flankenlinie des zu fräsenden Rades verlaufen. Der Wälzfräser und das Rad führen
kontinuierliche Drehbewegungen aus, so dass sich das Rad nach einer Umdrehung des Fräsers weiterdreht.
Zusätzlich führt der Fräser die Vorschubbewegung längs der Zahnbreite parallel zur Werkstückachse
aus.
Das Wälzstoßverfahren ist besonders für Innenverzahnungen geeignet. Als Werkzeug wird ein
gerad- oder schrägverzahntes Schneidrad mit hinterschliffenden Zahnflanken und hinterschliffenem
Außendurchmesser verwendet. Beim Abwälzen führt das Schneidrad eine hin- und hergehende
Stoßbewegung aus.
Neben dem „Wälzfräser“ und dem „Schneidrad“ können Sie auch die „Konstruierte Evolvente“ als
Werkzeug auswählen. Mit der konstruierten Evolvente wird Ihnen die Zahnformberechnung für innenverzahnte
Stirnräder ermöglicht, welche mit Schneidrädern nicht mehr herstellbar sind. Dies trifft insbesondere für
Anwendungen in der Feinwerktechnik zu. Mit dieser Werkzeugart ist auch die Zahnformerzeugung mit einem
konstanten Fußrundungsradius möglich.
Hinweis: In dem Kapitel 8.3.1 finden Sie jeweils eine Abbildung zum Wälzfräser und Schneidrad.
Das Werkzeug-Bezugsprofil ist das Gegenprofil zum Stirnrad-Bezugsprofil. Die folgenden genormten Werkzeug-Bezugsprofile stehen Ihnen für die Berechnung zur Verfügung und können über die folgende Listbox ausgewählt werden:

Um Schleifkanten am Zahnfuß zu vermeiden, kann man spezielle Vorbearbeitungswerkzeuge mit einem Protuberanzprofil einsetzen. Mit diesem Werkzeug wird ein geringer Unterschnitt bzw. eine Restunterwühlung erzeugt, so dass beim anschließenden Schleifen der Zahnflanken Kerben vermieden werden können.
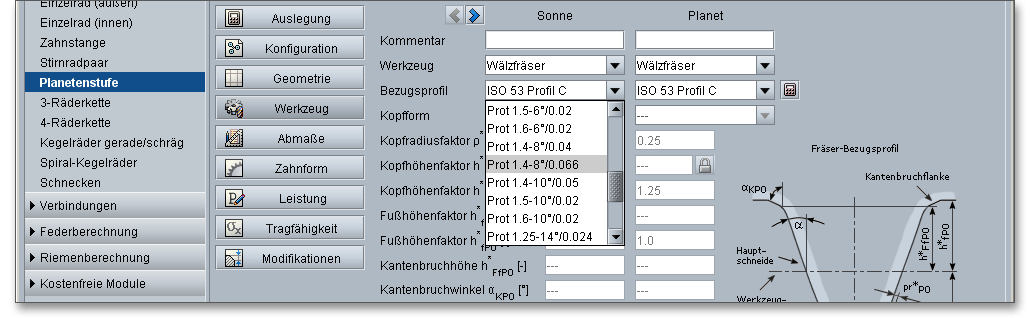
Über die Listbox lassen sich die folgenden Beispiele für Protuberanzprofile auswählen:
Hinweis: Wenn Sie in der Listbox den Eintrag „Eigene Eingabe“ auswählen, werden der Kopfrundungsradius,
die Kopfhöhe und die Fußhöhe aktiviert. Sie können so schnell das Werkzeug-Bezugsprofil individuell
vorgeben.
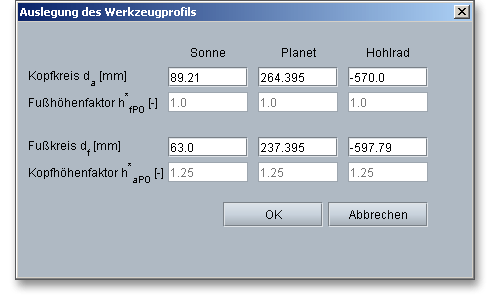
Für den Fall, dass Sie mit Sonderwerkzeugen arbeiten, bietet die eAssistant-Software Ihnen hier eine einfache und komfortable Lösung. Wie bereits oben erwähnt, kann das Werkzeug-Bezugsprofil in der Listbox über „Eigene Eingabe“ festgelegt werden. Klicken Sie auf den Taschenrechner-Button, dann können Sie den Kopfkreis sowie den Fußkreis für Sonne, Planet und Hohlrad ändern und sich die dafür notwendigen Kopf- und Fußhöhenfaktoren des Werkzeug-Bezugsprofils vorschlagen lassen.
Übernehmen Sie diese Eingabewerte mit dem Button „OK“, so erscheint in der Listbox der Eintrag „Eigene Eingabe“. Die Kopfhöhenänderung wird dabei auf den Wert „0“ gesetzt.
Wählen Sie für die Kopfform „Vollradius“ oder „Radius mit Gerade“ aus der Listbox aus. In der Regel nutzt
man „Radius mit Gerade“.
eAssistant bietet eine Funktionalität für Werkzeuge mit verschobener Profilbezugslinie. Neben dem
Kopfhöhenfaktor \(h^{*}_{aMP0}\) des verschobenen Profils wird auch der Fußhöhenfaktor \(h^{*}_{fMP0}\) mit angezeigt und im Protokoll
ausgegeben. Zusätzlich kann dieser über die Schloss-Funktion so vorgegeben werden, dass der
Fußhöhenfaktor \(h^{*}_{fP0}\) des umgerechneten nicht verschobenen Bezugsprofils gemäß Definition DIN 867 immer 1,0
ist. Im Kapitel 8.3.4 finden Sie eine Abbildung.
Mit der Definition der Kantenbruchflanke können entsprechende Wälzfräser vorgegeben werden. Diese
erzeugen beim Abwälzprozess einen Kopfkantenbruch. Mit der Option „Kopfüberschneidung“ werden die
Kopfkreisdurchmesser direkt mit dem Fußhöhenfaktor des Werkzeuges festgelegt. Ein nachträgliches
Abdrehen des Kopfkreisdurchmessers ist damit nicht möglich. Gleichzeitig ergeben sich dann
die Kopfkreisabmaße analog zu den Fußkreisabmaßen direkt aus den Zahndickenabmaßen. Die
eAssistant 3D-CAD-PlugIns für verschiedene CAD-Systeme unterstützen diese Funktion, so dass auch im
3D-Modell die Kantenbruchflanke berücksichtigt wird.
Protuberanzen werden als Flankenaufmaß für das Schleifen der Zahnflanke benutzt und werden durch die Verwendung entsprechend ausgebildeter Werkzeuge im Zahnfußbereich erzeugt. Durch das Wälzstoßen bzw. Abwälzfräsen mit den Protuberanzwerkzeugen bleibt auf der Zahnflanke eine Nachbearbeitungsschicht stehen. Diese Schicht wird anschließend durch Schleifen bzw. Schaben entfernt. Beim Abtragen dieser Schicht berührt das Werkzeug die Zahnfußausrundung nicht, wodurch Kerben und Schleifrisse im Zahnfußgrund vermieden werden. Eine Abweichung im Zahnfußbereich vom Profil zur Vermeidung von Schleifabsätzen ist üblich und zulässig. Auf Grund vom Schleifaufmaß muss man eine Restunterwühlung zulassen. Damit keine oder keine wesentliche Kürzung des evolventischen Profils vorliegt, ist eine größere Zahnfußtiefe erforderlich. Die folgende Tabelle zeigt eine modulabhängige Festlegung zur Restunterwühlung.
| Modulabhängige Restunterwühlung \(s_{pr}\) für geschliffene Verzahnungen1
| |||||
| Modul \(m\) | Bearbeitungs- | Restunter- | Protuberanz | Kopfhöhe | Kopfrundungsradius |
| zugabe \(q\) | wühlung \(s_{pr}\) | \(pr^{*}_{P0}\) | \(h^{*}_{aP0}\) | \(\rho ^{*}_{aP0}\) | |
| 2 | 0,160 | 0,100 | 0,260 | 2,900 | 0,500 |
| 2,5 | 0,170 | 0,110 | 0,280 | 3,625 | 0,625 |
| 3 | 0,180 | 0,120 | 0,300 | 4,350 | 0,750 |
| 4 | 0,200 | 0,140 | 0,340 | 5,800 | 1,000 |
| 5 | 0,220 | 0,160 | 0,380 | 7,250 | 1,250 |
| 6 | 0,240 | 0,180 | 0,420 | 8,700 | 1,500 |
| 7 | 0,260 | 0,200 | 0,460 | 10,150 | 1,7500 |
| 1 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl
Hanser Verlag, München, Wien, 2. Ausgabe 2010, S. 68, Tab.: 2.1/2
| |||||
Im Berechnungsmodul kann eine Bearbeitungszugabe je Zahnflanke berücksichtigt werden. Ein Vorverzahnungswerkzeug lässt für das nachfolgende Fertigverzahnen eine Bearbeitungszugabe \(q\) auf den Flanken und/oder Fuß stehen. Eine Bearbeitungszugabe ist der kleinste Abstand zwischen den Evolventen und der Vor-Verzahnung.
Wird das Werkzeug-Bezugsprofil mit Protuberanz gewählt oder eingegeben, so bezieht sich die Bearbeitungszugabe auf die Flanken. Wird die Bearbeitungszugabe bei einem Werkzeug-Bezugsprofil ohne Protuberanz vorgegeben, so erhalten Flanken und Fuß das entsprechende Aufmaß. Die maximalen Bearbeitungszugaben der einzelnen Verfahren lassen sich wie folgt einteilen:
| Maximale Bearbeitungszugaben2
| |
| Bearbeitungszugabe pro Zahnflanke | Verfahren |
| \(<\) 0,05 (0,10) mm | Feinbearbeitung duch Kaltwalzen, Wälzschaben, Wälzhohnen, Wälzlappen |
| 0,05 bis 0,5 (1,5) mm | Wälzschleifen, Profilschleifen, (Wälzhonen) |
| \(>\) 0,5 mm, Vorverzahnen | Urformen, Umformen, Spanen mit geometrisch bestimmter Schneide außer Wälzschaben, Wälz- und Profilschleifen in Sonderfällen |
| 2 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl
Hanser Verlag, München, Wien, 1996, S. 638
| |
Hinweis: Weitere detaillierte Informationen zur Protuberanz und zur Bearbeitungszugabe finden Sie in den
Kapiteln 8.3.6 und 8.3.7.
In dieser Eingabemaske werden die Verzahnungsqualität sowie die Abmaß- und Toleranzreihe für Sonne, Planet und Hohlrad festgelegt. Desweiteren werden die oberen und unteren Zahndicken- und Zahnweitenabmaße automatisch vom Programm berechnet. Die Zahndickenabmaße können allerdings auch direkt eingegeben werden. Die notwendige Messzähnezahl sowie der Messkörperdurchmesser werden ermittelt oder können individuell vorgegeben werden. Eine Herstellung von Werkstücken mit exakten Nennmaßen ist unmöglich, daher sind Abweichungen vom theoretischen Sollmaß zulässig. In vielen Anwendungsgebieten werden Sonne, Planeten und Hohlrad unabhängig voneinander gefertigt und müssen ohne große Anpassungen aufeinander abgestimmt sein. Neben der DIN 3961 für Verzahnungstoleranzen/Verzahnungsqualitäten stehen jetzt auch die DIN 58405 für die Feinwerktechnik sowie die ISO 1328 und die ANSI/AGMA 2015 zur Verfügung.
Hinweis: Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung für Sonne, Planet und
Hohlrad. Die Bemerkung erscheint dann später auch im Protokoll.
Die Qualität ist nach wirtschaftlichen Gesichtspunkten in Abhängigkeit vom Verwendungszweck und somit vom Fertigungsverfahren festzulegen. In den DIN-Verzahnungsnormen werden die qualitativen Grenzen für die einzelnen Abweichungen in 12 Verzahnungsqualitäten festgelegt und in der Reihenfolge der Genauigkeit von 12 bis 1 bezeichnet. Die Qualität 1 bezeichnet dabei die feinste Genauigkeit, die Qualität 12 die gröbste Genauigkeit. Die Verzahnungsqualitäten 1 bis 4 werden vorwiegend für Lehrzahnräder verwendet, die Klassen 5 bis 12 für Getrieberäder. Kapitel 8.4.1 zeigt eine Übersicht über die Herstellungsverfahren in Abhängigkeit von der Qualität. Hier finden Sie auch eine Tabelle mit Anhaltswerten für die Wahl der Verzahnungsqualitäten und Toleranzklassen. Die einzelnen Qualitäten lassen sich jeweils für Sonne, Planet und Hohlrad aus der Listbox auswählen.
Für die Verzahnungstoleranzen/Verzahnungsqualitäten stehen auch DIN 58405 für die Feinwerktechnik
sowie die ISO 1328 und die ANSI/AGMA 2015 zur Verfügung. Bei ISO 1328 und ANSI/AGMA 2015 lassen sich
jeweils zwei Qualitäten auswählen. Die erste Qualität ist vergleichbar mit den nach DIN 3961
zulässigen Toleranzen, der zweite Wert beeinflusst die Zweiflanken-Wälzabweichung sowie die
Rundlaufabweichungen.
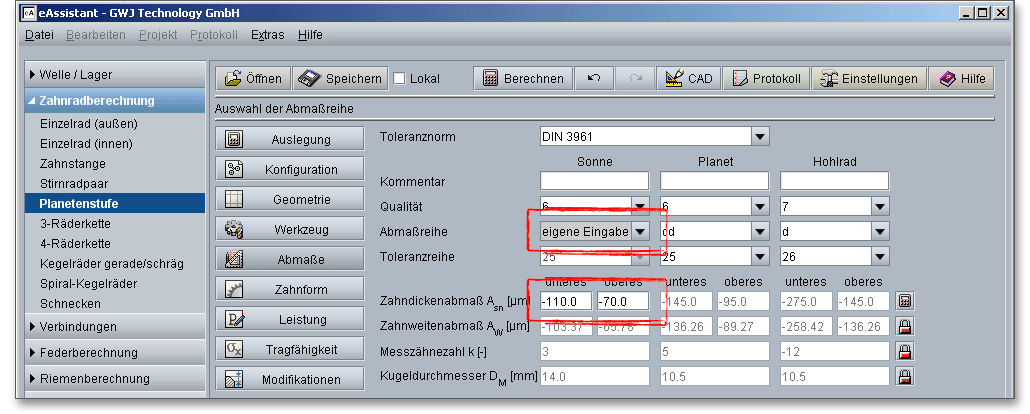
In dem DIN-Getriebe-Passsystem kennzeichnet man den Abstand des Toleranzfeldes vom Nennmaß mit einem Buchstaben, seine Breite mit einer Zahl. Bei Verzahnungen gibt es nur Spielpassungen, deshalb kommen nur die Buchstaben h bis a vor. Wählen Sie in der Listbox den Eintrag „eigene Eingabe“, dann wird das Eingabefeld für die Zahndickenabmaße freigeschaltet und Sie haben die Möglichkeit, individuelle Daten festzulegen. Weiterhin ist nun auch der Schloss-Button neben dem Eingabefeld für die Zahnweitenabmaße aktiv.
Infolge einer größeren Ausdehnung der Zahnräder als Wärmequelle gegenüber dem Gehäuse ist ohne elastische Elemente kein spielfreier Einbau möglich. Es müssen deshalb die Zahndickenabmaße so festgelegt werden, dass kein Klemmen der Zahnräder auftritt. Um dieses Klemmen der Zahnräder beim Betrieb zu vermeiden, müssen die Zähne um einen Mindestbetrag - das obere Zahndickenabmaß \(A_{sne}\) - dünner als die Nenn-Zahndicken sein. Die Verkleinerung der Zahndicken nennt man auch Zahndickenabmaß \(A_{sn}\). Die Zähne von Außen- und Innenverzahnungen müssen negative Zahndickenabmaße aufweisen. So kann ein Flankenspiel erreicht werden. Die größte Zahndicke ist durch das obere Zahndickenabmaß \(A_{sne}\), die kleinste Zahndicke durch das untere Zahndickenabmaß \(A_{sni}\) begrenzt. Klicken Sie auf das Taschenrechner-Symbol, um die Zahndickenabmaße rückwärts, zum Beispiel aus gemessenen Werten oder vorgegebenen Prüfmaßen, zu berechnen.
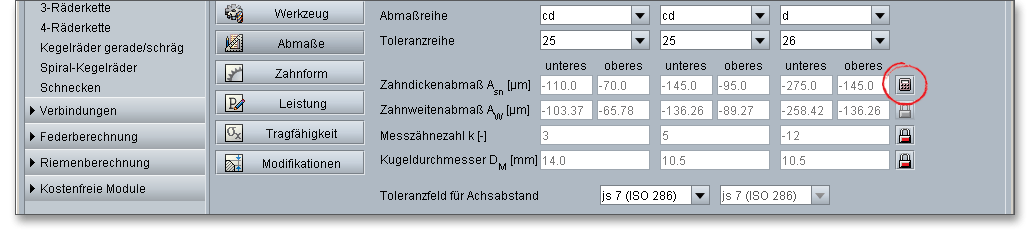
Ein neues Fenster öffnet sich.
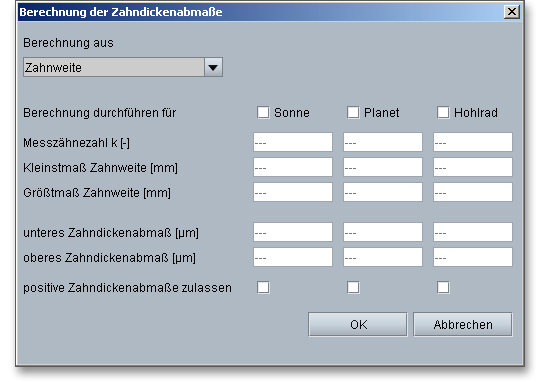
Aktivieren Sie mit einem Häkchen jeweils Sonne, Planet und Hohlrad, vervollständigen Sie die
Eingabewerte und klicken Sie auf den Button „OK“. Der Schloss-Button neben dem Eingabefeld
für die Zahnweitenabmaße wird freigegeben. Darüber können Sie bei Bedarf optional zu den
Zahndickenabmaßen auch die Zahnweitenabmaße beeinflussen. Bei Innenverzahnungen ist zu beachten,
dass die Werte für Messzähnezahl, Zahnweitenmaße und Rollen- bzw. Kugelmaße stets negativ
sind.
Das Zahnweitenabmaß \(A_{W}\) ist der Unterschied zwischen dem Ist- und Nennmaß der Zahnweite \(W{_k}\). Das Istmaß der Zahnweite wird bei Außenräder durch negative Abmaße kleiner als das Nennmaß für den spielfreien Eingriff. Wie auch bei dem Zahndickenabmaß gibt es hier ein oberes und ein unteres Zahnweitenabmaß, die mit \(A_{We}\) und \(A_{Wi}\) definiert sind. Bei einer eigenen Eingabe der Zahndickenabmaße können optional die Zahnweitenabmaße vorgegeben werden. Bei dieser eigenen Eingabe wird der Schloss-Button neben dem Eingabefeld für die Zahnweitenabmaße aktiviert. Diese können somit geändert werden.
Die Zahndicke ist ein Bogenstück und kann nicht direkt gemessen werden. Deshalb werden unterschiedliche Messverfahren genutzt. Die Zahndicke kann so auf verschiedene Weise gemessen werden:
Die Zahnweite \(W_{k}\) ist das Maß, dass sich zwischen zwei parallelen Ebenen ergibt, die je eine rechte und linke Flanke über mehrere Zähne \(k\) hinweg berühren. Bei Stirnrädern wird die Zahndicke am häufigsten mit Hilfe der Zahnweite gemessen. Die Zahndicke kann durch manuelle Geräte sehr einfach erfasst werden. Der Vorteil dabei ist auch, dass das Passmaß bereits während einer Serienfertigung beeinflusst werden kann. Das Berechnungsmodul gibt Ihnen die Messzähnezahl, also die Anzahl der Zähne, über die die Zahnweite zu messen ist, vor. Über den Schloss-Button können Sie jedoch das Eingabefeld freischalten und einen eigenen Wert für die Messzähnezahl angeben. Klicken Sie erneut auf den Button, wird der ursprüngliche Wert wieder eingesetzt.

Das diametrale Prüfmaß \(M_{d}\) ist bei einem Außenrad das größte äußere Maß. Dieses Maß wird über zwei Messkörper gemessen. Die Messkörper sind dabei Kugeln (Diametrales Zweikugelmaß \(M_{dK}\)) oder Rollen (Diametrales Zweirollenmaß \(M_{dR}\)), die in gegenüberliegende Zahnlücken gelegt werden. Die Prüfung mit Hilfe der Messkörper stellt eine sehr genaue Prüfmethode dar. Das Zweirollenmaß ist nur bei Geradverzahnungen und außenverzahnten Schrägzahnrädern anwendbar. Bei den diametralen Prüfmaßen unterscheidet man:
Das diametrale Zweikugelmaß \(M_{dK}\) ist bei einem Außenrad das größte äußere Maß. Dieses wird über die zwei Kugeln gemessen, die in die am weitesten voneinander entfernten Zahnlücken gelegt werden. Beide Kugeln müssen sich in der gleichen Ebene senkrecht zur Radachse befinden. Bei einem Hohlrad ist das diametrale Zweikugelmaß das kleinste innere Maß zwischen zwei Kugeln. Auch für die diametralen Prüfmaße gibt das Berechnungsmodul Ihnen den Kugeldurchmesser bereits vor. Der Durchmesser der Kugeln bzw. Rollen wird jeweils definiert mit \(D_{M}\). Über den Schloss-Button können Sie das Eingabefeld freischalten und einen eigenen Wert für den Kugel- bzw. Rollendurchmesser angeben. Klicken Sie erneut auf den Button, wird der ursprüngliche Wert wieder eingesetzt.

Hinweis: In dem Kapitel 8.4.5 finden Sie die jeweiligen Abbildungen zur Zahnweitenabmessung sowie zu den
diametralen Prüfmaßen.
Um ein Klemmen der Räder zu vermeiden, muss zwischen den Flanken stets ein Spiel vorhanden sein. Wesentliche Einflussgrößen auf das Flankenspiel sind der Achsabstand und die Passgrößen der Verzahnung. Das Getriebe-Passsystem definiert die Abweichungen des Achsabstandes mit dem Flankenspiel. In dem Passsystem der DIN wird nur ein Toleranzfeld des Achsabstandes angewendet. Beim Achsabstand werden die Abmaße für das „JS“-Feld angegeben. Diese entsprechen genau den ISO-Grundtoleranzen. Die Flankenspiele sind abhängig vom Zahndickenabmaß, Zahnweitenabmaß und Achsabstand. Mit der Änderung des Achsabstandes ändert sich dann auch das jeweilige Flankenspiel.

Wählen Sie in der Listbox die Option „Eigene Eingabe“, dann haben Sie die Möglichkeit, das obere und
untere Achsabstandsabmaß für Sonne-Planet festzulegen. Betätigen Sie mit der Enter-Taste Ihre Eingaben.
Die Flankenspiele werden dann automatisch berechnet.
Das Achsabstandsmaß \(A_{a}\) ist die zulässige Abweichung des Achsabstandes \(a\) im Getriebe von dem
Nennmaß des Achsabstandes. Die Abmaße sind mit \(\pm \) angegeben, um bei Getrieben mit mehreren
Achsen keine unzulässig großen Abweichungen von den Nennmaßen der Achsabstände zu
erhalten.
Mit Hilfe des Flankenspiels lassen sich Herstellungs- und Einbauungenauigkeiten ausgleichen und ein Klemmen
der Zahnräder wird vermieden. Die Größe des Flankenspiels hängt, von Verzahnungsfehlern abgesehen,
von der Zahndicke und vom Achsabstand der Räder ab. Auch Erwärmung, Verformung der Getriebeelemente
und die Verlagerung des Gehäuses beeinflussen das Flankenspiel. Diese Einflüsse müssen zusätzlich bei
der Festlegung der Zahndickenabmaße berücksichtigt werden. Das DIN-System geht von einem konstanten
Achsabstand aus und schafft die verschiedenen Flankenspiele durch eine Änderung der Zahndicke. Das
Flankenspiel ist am größten beim untersten Zahndickenabmaß \(A_{sni}\) und am kleinsten beim oberen
Zahndickenabmaß \(A_{sne}\). Das Flankenspiel wird weiterhin durch die Fehler der Teilung und der Flankenform
beeinflusst sowie von der Erwärmung, Verformung der Getriebeelemente und Verlagerung des
Gehäuses.
Das Verdrehflankenspiel \(j_{t}\) ist das auf den Wälzkreis bezogende Spiel. Das Verdrehflankenspiel ist die Länge des Wälzkreisbogens, um den sich ein Rad gegenüber dem anderen Rad verdrehen lässt. Das Radialspiel ist die Differenz des Achsabstandes zwischen dem Betriebszustand und dem Zustand des spielfreien Eingriffes. Kapitel 8.4.7 veranschaulicht das Achsabstandsabmaß sowie Normal- und Verdrehflankenspiel anhand von Abbildungen.
Ein besonderes Highlight des Berechnungsmoduls ist die Darstellung der exakt berechneten Zahnform mit der parallelen Animation und Simulation der Zahneingriffe von Sonne-Planet und Planet-Hohlrad. Für diese Darstellung können die kleinsten, mittleren und größten Abmaße für die Zahndicken, den Kopfkreis und den Achsabstand gewählt werden.
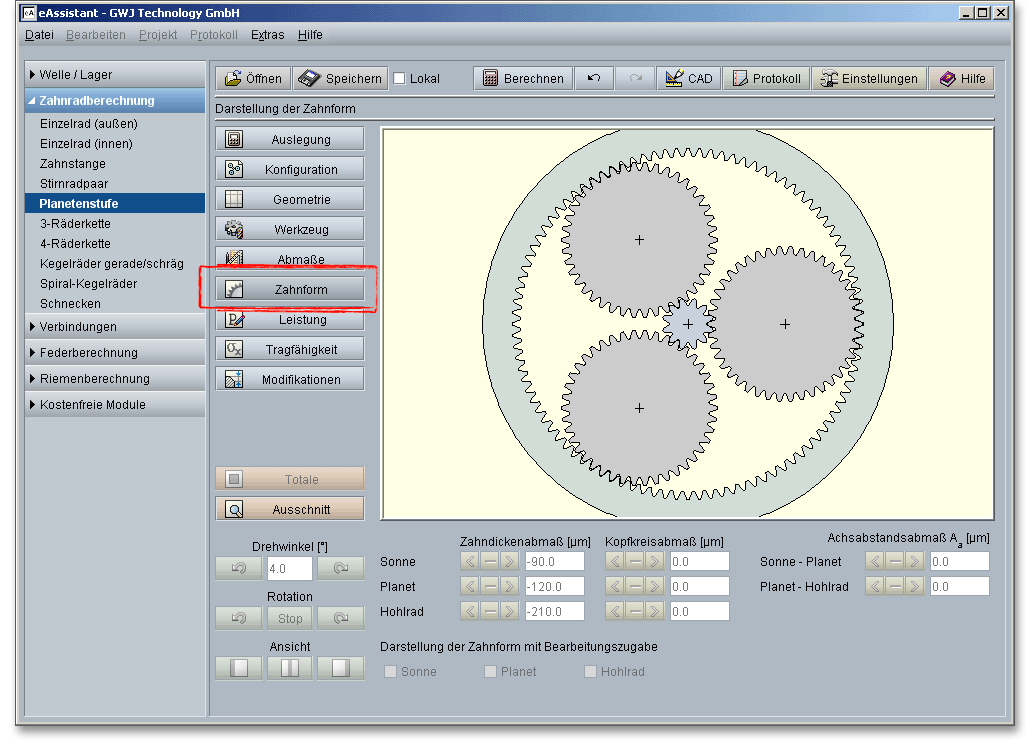
Hinweis: Bitte beachten Sie, dass die Daten in der Zahnform in die spätere DXF-Ausgabe und in die
CAD-Erzeugung übernommen werden. Wenn Sie zum Beispiel in der Zahnform das Zahndickenabmaß oder
das Achsabstandsabmaß verändern, so wird jeweils die letzte Einstellung, die Sie an der Zahnform
vornehmen, in die „DXF-Ausgabe“ oder die eAssistant CAD-PlugIns übertragen. Alle weiteren
Informationen zum 2D-DXF-Format und zu den einzelnen CAD-PlugIns erhalten Sie in dem Kapitel „Button
CAD“.
Um das gesamte Planetengetriebe darzustellen, klicken Sie auf den Button „Zahnform“.
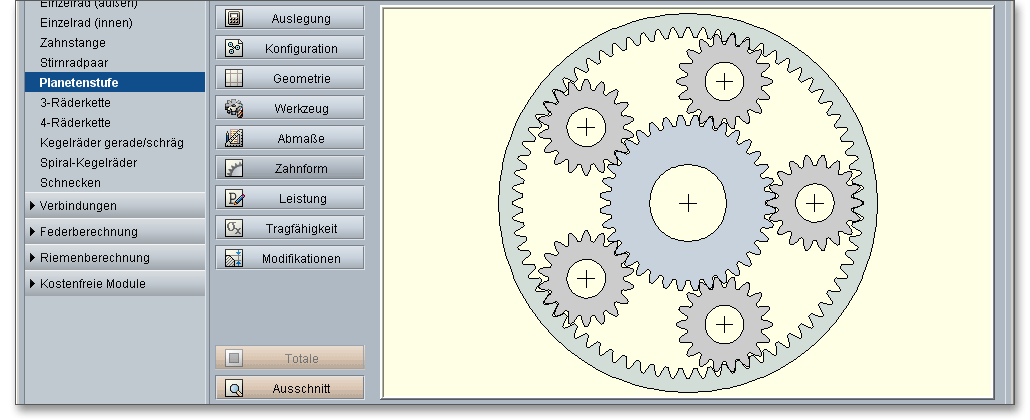
Mit einen Klick auf den Button „Ausschnitt“ lässt sich der detaillierte Zahneingriff der Paarungen Sonne-Planet und Planet-Hohlrad in der Vergrößerung darstellen. Die „Darstellung des Zahneingriffs“ bietet Ihnen die Möglichkeit, das Zahnspiel sowie den Zahneingriff mit Hilfe der Zahndicken-, Kopfkreis- sowie Achsabstandsabmaße näher zu betrachten und den Einfluss aller genannten Größen detailliert zu untersuchen. Klicken Sie auf den Button „Totale“, wird Ihnen wieder das komplette Planetengetriebe angezeigt.
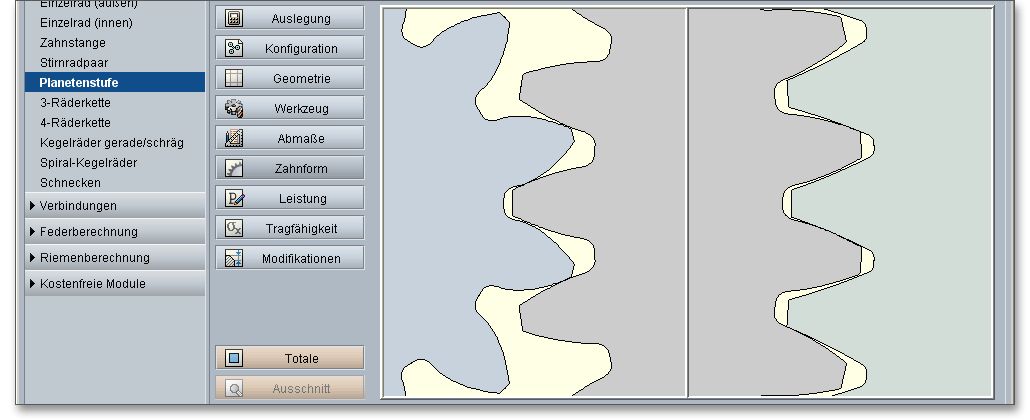
Wenn Sie auf den Button „Ausschnitt“ klicken, bekommen Sie standardmäßig die Darstellung des
Zahneingriffs der beiden Paarungen Sonne-Planet und Planet-Hohlrad. Sie können sich die Zahneingriffe aber
auch einzeln anzeigen lassen, also nur den Eingriff Sonne-Planet oder Planet-Hohlrad (siehe Kapitel 9.7.5
„Ansicht“).
Geben Sie hier für die Drehung des Stirnradpaares einen Drehwinkel ein.

|
| Drehung des antreibenden Rades entgegen dem Uhrzeigersinn |
|
| Drehung des antreibenden Rades im Uhrzeigersinn |
Klicken Sie auf einen der beiden Pfeile, erfolgt eine kontinuierliche Drehung der Stirnräder.

|
| Kontinuierliche Drehung des antreibenden Rades entgegen dem Uhrzeigersinn |
|
| Kontinuierliche Drehung des antreibenden Rades im Uhrzeigersinn |
|
| Drehung wird gestoppt. |
Lassen Sie sich hier den Zahneingriff von Sonne-Planet und Planet-Hohlrad parallel oder einzeln anzeigen. In beiden Darstellungen kann der Zahneingriff anhand der Animation näher betrachtet werden.

|
| Nur den Zahneingriff von Sonne und Planet betrachten. |
|
| Den Zahneingriff der Paarungen Sonne-Planet und Planet-Hohlrad darstellen. |
|
| Nur den Zahneingriff von Planet-Hohlrad darstellen. |


Klicken Sie auf den Button „Ausschnitt“, um den detaillierten Zahneingriff darzustellen. Jetzt besteht die Möglichkeit, das bereits in der Hauptmaske „Abmaße“ angegebene Zahndickenabmaß für Sonne, Planet und Hohlrad innerhalb der Toleranzgenzen zu verändern. Diese Veränderungen werden Ihnen sofort in dem Darstellungsfenster angezeigt. Für die Darstellung des Zahneingriffs können jeweils die unteren, mittleren und oberen Abmaße für die Zahndicke für Sonne, Planet und Hohlrad gewählt werden.

Die beiden Pfeile kennzeichnen das untere und das obere Abmaß. Bei der jeweils aktiven Eingabe wird der Pfeil grau hinterlegt. Klicken Sie auf den linken Pfeil, erhalten Sie die Darstellung mit dem unteren Zahndickenabmaß. Der rechte Pfeil liefert Ihnen die Ansicht mit dem oberen Zahndickenabmaß. Der mittlere Button zeigt Ihnen im Darstellungsfenster das mittlere Zahndickenabmaß an. Die Zahndickenabmaße können auch individuell innerhalb der Grenzen, also zwischen dem oberen und unterem Abmaß, eingegeben werden.

Hinweis: Wenn Sie in der Eingabemaske „Abmaße“ die unteren und oberen Zahndickenabmaße für Sonne,
Planet und Hohlrad über das Taschenrechner-Symbol individuell festgelegt haben, dann erscheinen die
manuell definierten Werte hier als unteres und oberes Zahndickenabmaß.
Klicken Sie auf den Button „Ausschnitt“, um den detaillierten Zahneingriff darzustellen. Jetzt besteht die Möglichkeit, das bereits in der Hauptmaske „Geometrie“ angegebene Kopfkreisabmaß für Sonne, Planet und Hohlrad innerhalb der Toleranzgenzen zu verändern. Diese Veränderungen werden Ihnen sofort in dem Darstellungsfenster angezeigt. Für die Darstellung des Zahneingriffs können jeweils die unteren, mittleren und oberen Abmaße für Sonne, Planet und Hohlrad gewählt werden.

Die beiden Pfeile kennzeichnen das untere und das obere Abmaß. Bei der jeweils aktiven Eingabe wird der Pfeil grau hinterlegt. Klicken Sie auf den linken Pfeil, erhalten Sie die Darstellung mit dem unteren Kopfkreisabmaß. Der rechte Pfeil liefert Ihnen die Ansicht mit dem oberen Kopfkreisabmaß. Der mittlere Button zeigt Ihnen im Darstellungsfenster das mittlere Kopfkreisabmaß an. Die Kopfkreisabmaße können auch individuell innerhalb der Grenzen, also zwischen dem oberen und unterem Abmaß, eingegeben werden.

Hinweis: Wenn Sie in der Eingabemaske „Geometrie“ die unteren und oberen Kopfkreisabmaße für Sonne,
Planet und Hohlrad über das Schloss-Symbol individuell festgelegt haben, dann erscheinen die manuell
definierten Werte hier als unteres und oberes Kopfkreisabmaß.
Klicken Sie auf den Button „Ausschnitt“, um den detaillierten Zahneingriff darzustellen. Sie haben jetzt die Möglichkeit, das bereits in der Hauptmaske „Abmaße“ angegebene Achsabstandsabmaß für die Paarung Sonne-Planet innerhalb der Toleranzgenzen zu verändern. Diese Veränderungen werden Ihnen sofort in dem Darstellungsfenster angezeigt. So können Sie den Lauf der Räder mit den unterschiedlichen Achsabständen anschaulich untersuchen. Für die Darstellung des Zahneingriffs können jeweils die unteren, mittleren und oberen Abmaße für die Paarungen gewählt werden.

Die beiden Pfeile kennzeichnen das untere und das obere Abmaß. Bei der jeweils aktiven Eingabe wird der Pfeil grau hinterlegt. Klicken Sie auf den linken Pfeil, erhalten Sie die Darstellung mit dem unteren Achsabstandsabmaß. Der rechte Pfeil liefert Ihnen die Ansicht mit dem oberen Achsabstandsabmaß. Der mittlere Button zeigt Ihnen im Darstellungsfenster das mittlere Achsabstandsabmaß an.
Das Achsabstandsabmaß kann auch individuell innerhalb der Grenzen, also zwischen dem oberen und unterem Abmaß, eingegeben werden.

Hinweis: Wenn Sie in der Eingabemaske „Abmaße“ den unteren und oberen Achsabstand für die
Paarung Sonne-Planet über den Eintrag „eigene Eingabe“ aus der Listbox „Toleranzfeld für
Achsabstand“ individuell festgelegt haben, dann erscheinen die manuell definierten Werte hier als unteres und
oberes Achsabstandsabmaß.
Neben der Geometrieberechnung werden die Drehmomente, Drehzahlen inklusive der Relativdrehzahl des
Planeten, sowie die Leistungen, Wälzleistungen und Kupplungsleistungen bestimmt. Zusätzlich werden die
Stegumfangskraft sowie die Planetenzentrifugalkraft ermittelt. Beide Werte werden im Berechnungsprotokoll
ausgegeben. Ein Vorteil des Planetengetriebes besteht darin, dass die Leistung über mehrere
Planetenräder übertragen wird. Diese Leistungsteilung bewirkt, dass die mechanische Belastbarkeit eines
Getriebes gesteigert wird und große Übersetzungsstufen sowie große Drehmomente möglich werden.
Im Idealfall teilen sich die Umfangskräfte gleichmäßig auf die Zahneingriffe mit den Planeten
auf.
In einem Planetengetriebe werden die Kräfte und Drehmomente über Achsen und Wellen weitergleitet. Die Planetenräder des Getriebes können sowohl auf einer Achse als auch auf einer Welle gelagert sein.
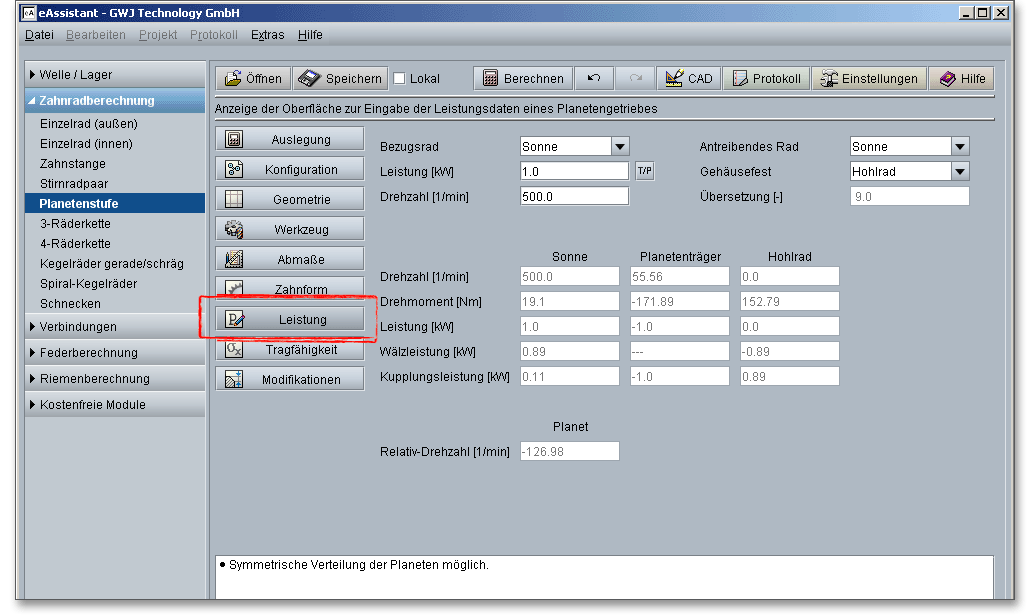
Über den nebenstehenden Button „T/P“ können Sie zwischen der Eingabe für das Drehmoment und der Eingabe für die Leistung hin und her wechseln. Wenn Sie auf den Button „T/P“ klicken, können Sie entweder das Drehmoment oder die Leistung eingeben bzw. umrechnen lassen. Die Bezeichnung des Eingabefeldes ändert sich dann entsprechend in Drehmoment oder Leistung. Maßgeblich ist, dass drei im Gleichgewicht stehende Drehmomente vorhanden sind. Nach dem Energieerhaltungssatz müssen die Summen der Teilleistungen gleich Null sein. Die Drehmomente haben positive und negative Vorzeichen. Zwei der drei Drehmomente besitzen jeweils das gleiche Vorzeichen. Bei einer Antriebswelle sind die Vorzeichen von Drehzahl und Drehmoment gleich, bei einer Abtriebswelle jedoch ungleich. Sobald ein Drehmoment festliegt, ergeben sich die beiden anderen Momente automatisch.

Eine Antriebsleistung \(P_{A}\), die zugeführte Leistung, ist immer positiv und eine Abtriebsleistung, die abgegebene Leistung, ist immer negativ. Bei einer Antriebswelle haben Drehzahl und Drehmoment das gleiche Vorzeichen, bei einer Abtriebswelle sind die Vorzeichen voneinander verschieden. Die Flussrichtung für die Wellenleistung liegt fest: die äußere Leistung fließt immer von der Antriebswelle zur Abtriebswelle.

Bei einem Planetengetriebe wird zwischen Wellenleistung, Wälzleistung und Kupplungsleistung unterschieden.
Die Wälzleistung \(P_{W}\), das Produkt aus Umfangskraft \(F_{u}\) am Wälzkreis und Wälzgeschwindigkeit, ist eine
innere Leistung, die durch Abwälzen der Zahnräder übertragen wird und auftritt, wenn sich die
Zahnräder gegenüber dem Steg drehen. Bei einem ruhenden Steg wird die gesamte Leistung \(P\)
von den Zahnrädern als Wälzleistung \(P_{W}\) übertragen und die Wälzleistung \(P_{W}\) ist dann gleich der
Wellenleistung \(P\). Bei einem Planetengetriebe mit einem umlaufenden Steg ist die Wälzleistung \(P_{W}\) nicht
gleich der Wellenleistung \(P\). Wellenleistung und Wälzleistung unterscheiden sich um den Betrag der
Kupplungsleistung.
Hinweis: Durch die Wälzleistung treten Zahnreibungsverluste auf. Deshalb sollte der Wälzleistungsanteil bei
einer Leistungsübertragung so gering wie möglich gehalten werden. Je geringer die Wälzleistung, um so
besser ist der Verzahnungswirkungsgrad des Planetengetriebes.
Planetengetriebe übertragen die von außen zugeführte Wellenleistung \(P\) zu einem Teil als Wälzleistung \(P_W\) und
zum anderen Teil als Kupplungsleistung \(P_{k}\). Die Kupplungsleistung wird verlustfrei übertragen.
Drehzahlen gegenüber dem stets ruhenden Getriebegehäuse werden als absolute Drehzahlen bezeichnet.
Drehzahlen gegenüber einer Welle werden als Relativdrehzahlen bezeichnet.
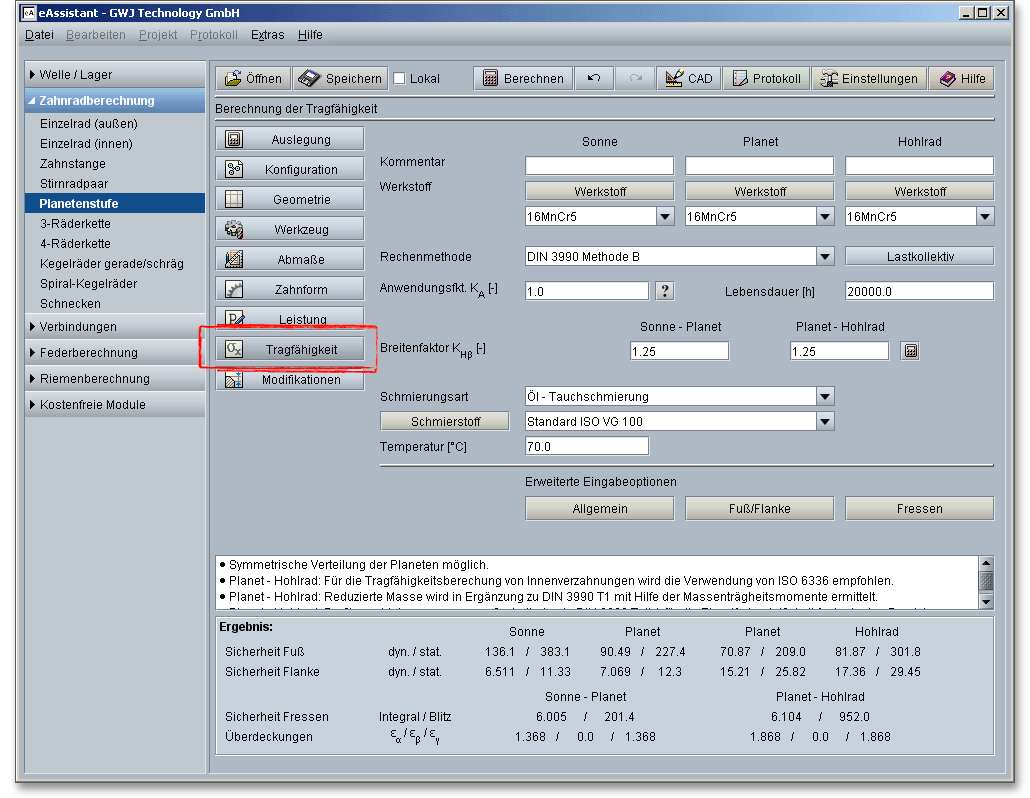
Für die Festigkeitsberechung der Stirnräder stehen die Methoden DIN 3990 Methode B, ISO 6336 Methode B, ANSI/AGMA 2101-D04 sowie VDI 2736 für Kunststoffverzahnungen zur Auswahl. Zunächst erhalten Sie Informationen zur DIN 3990 Methode B, anschließend folgen Erläuterungen zur ISO 6336 Methode B, ANSI/AGMA 2101-D04 und VDI 2736.
Bei Plantengetriebe muss zusätzlich noch die ungleichmäßige Lastverteilung auf die Planetenräder berücksichtigt werden. Bei der Berechnung der Tragfähigkeit geht es stets um die Überprüfung der:
Mit dem Modul können Sie die Zahnfuß-, Zahnflanken- sowie die Fresstragfähigkeit schnell und einfach überprüfen. Bei der Fresstragfähigkeit werden die Sicherheiten bezüglich des Integral- und Blitztemperatur-Kriteriums berechnet. Berücksichtigt werden die Materialeigenschaften, die Lebensdauer sowie die Schmierungsart und der entsprechend gewählte Schmierstoff. Die erweiterten Eingabeoptionen bieten die Möglichkeit, die Anzahl der Lastwechsel sowie die Rautiefe zu beeinflussen. Schleifkerben können in die Berechnung mit einbezogen werden, die Betriebsart wird über den Betriebsartenfaktor gewählt.
Die folgenden Faktoren berücksichtigen die wesentlichsten Einflüsse bei der Tragfähigkeitsberechnung:
Die Zahnfußtragfähigkeit ist die durch die zulässige Zahnfußbeanspruchung bestimmte Tragfähigkeit.
Ein Zahnbruch kann zum Beispiel aus einer Schleifkerbe resultieren. Wird die Beanspruchung
überschritten, brechen die Zähne meist am Zahnfuß aus. Ein Zahnbruch zerstört die gesamte
Verzahnung und führt somit zum Ausfall eines Getriebes. Laut DIN 3990 ist nach einem Zahnbruch ein
Betrieb mit verringerter Belastung möglich, wenn nur ein kleiner Teil eines oder mehrerer Zähne
ausgebrochen ist und die übrigen Teile der Verzahnung unbeschädigt sind. Zahnbruch ist ein
Ermüdungsschaden.
Günstig sind: positive Profilverschiebung (bei kleinen Zähnezahlen), Verwendung vergüteter oder
gehärteter Werkstoffe mit höherer Zahnfußfestigkeit, größere Zahnfußausrundung, größerer Modul,
größerer Eingriffswinkel, größere Zahnbreite
Die Grübchentragfähigkeit ist die durch die zulässige Flankenpressung bestimmte Tragfähigkeit.
Grübchenbildung ist ein Ermüdungsschaden und tritt hauptsächlich auf der Fußflanke auf. Bei einer
Grübchenbildung entstehen an der Oberfläche feine Risse, in die Öl eindringt. Beim Überrollen werden die
Öffnungen verschlossen und Materialteilchen herausgesprengt. Die Vertiefungen, die sich dadurch bilden,
werden auch Grübchen (bzw. Pitting) genannt. Diese Ausbröckelungen sind erst dann unzulässig, wenn die
Anzahl der Grübchen zunimmt oder die Grübchen größer werden. Grübchenfestigkeit ist ebenfalls ein
Ermüdungsschaden.
Günstig sind: große Zähnezahl, positive Profilverschiebung (bei kleinen Zähnezahlen), größerer
Eingriffswinkel, hohe Flankenhärte, Nitrierhärten, zäheres Öl
Durch Mangel an Schmierstoff oder durch ein Zusammenbrechen des Schmierfilms können zwischen den Zahnflanken Verschleißerscheinungen auftreten. Diese Schadensform wird „Fressen“ genannt. Besonders bei mechanisch und thermisch hochbelasteten Verzahnungen tritt das Problem des Fressens auf. Infolge des Fressens steigen bei schnelllaufenden Getrieben die Temperatur, die Zahnkräfte sowie die Geräusche so stark an, dass der Schmierfilm zwischen den Zahnflanken abreißt. Die metallischen Flächen reiben aufeinander und es kommt zu kurzzeitigen örtlichen Verschweißungen der Flanken. Schließlich kommt es wegen der starken Flankenschäden zum Zahnbruch. Im Gegensatz zum Zahnbruch und zur Grübchenbildung ist das Fressen kein Ermüdungsschaden. Fressen kann ganz plötzlich auftreten. Bereits eine einzige kurze Überlastung kann zu einem Fressschaden führen und somit zum Ausfall der Zahnräder. Die Gefahr des Auftretens von Fressschäden wird beeinflusst von:
Nach dem Auftreten eines Fressschadens neigen schnelllaufende Getriebe zu hohen dynamischen Zusatzkräften, die als Folge von Fressen gewöhnlich Grübchenbildung oder Zahnbruch verursachen. Die hohen Oberflächentemperaturen führen zum Zusammenbrechen des Schmierfilms. Fressen wird begünstigt durch:
Günstig sind: EP-Öle (Öle mit chemisch aktiven Zusätzen), geeignete Werkstoffauswahl, sorgfältiges
Einlaufen der Verzahnung, geringe Gleitgeschwindigkeit durch Zahnkopfkürzung oder kleineren
Modul
Wenn Sie auf den Button „Tragfähigkeit“ klicken, dann gelangen Sie in den Berechnungsbereich für die Tragfähigkeit. Sie werden bemerken, dass im Moment alle Eingabe- oder Auswahlfelder deaktiviert sind. Sobald Sie in der Listbox „Rechenmethode“ „DIN 3990 Methode B“, „ISO 6336 Methode B (2006, 2019)“ „ANSI/AGMA 2101-D04“ oder „VDI 2736“ auswählen, werden alle Eingabefelder aktiviert. Für den Fall, dass Sie die Tragfähigkeitsberechnung nicht benötigen, kann diese somit „ausgeschaltet“ werden. Dadurch verringert sich der Umfang des Protokolls.
Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung für Sonne, Planet und Hohlrad. Die Bemerkung erscheint später im Protokoll im Bereich der Tragfähigkeit.
Wählen Sie hier den entsprechenden Werkstoff für Sonne, Planet und Hohlrad direkt aus der Listbox oder klicken Sie auf den Button „Werkstoff“ über den Sie anschließend in die Werkstoffdatenbank gelangen.

In der Werkstoffdatenbank erhalten Sie detaillierte Informationen zu den einzelnen Werkstoffen. Klicken Sie sich mit Hilfe der Cursor-Taste nach unten durch die Listbox. Somit lassen sich die einzelnen Werkstoffe anhand ihrer Eigenschaften miteinander vergleichen.
Für die Herstellung von Zahnrädern werden vorwiegend Stähle eingesetzt. Für Ritzel und Rad kann der
gleiche Vergütungsstahl eingesetzt werden. Bei der Werkstoffauswahl ist zu beachten, dass ungehärtete
Räder gleicher Härte nicht gepaart werden sollten, da hierbei große Neigung zum Fressen der Flanken
besteht. Ein gehärtetes oder nitriertes Rad \(HRC > 50\) glättet die Zahnflanken eines vergüteten Gegenrades, baut
dessen Formabweichungen ab und erhöht dadurch die Grübchentragfähigkeit. Bei einer Paarung gehärteter
Räder sind keine Härteunterschiede erforderlich.
Einsatzstahl: Hier handelt es sich um Qualitäts- und Edelstähle mit einem niedrigen Kohlenstoffgehalt. Sie
werden im Bereich der Randzone aufgekohlt, gegebenenfalls gleichzeitig aufgestickt und anschließend
gehärtet. Der Stahl hat nach dem Härten in der Randschicht eine hohe Härte und einen guten
Verschleißwiderstand, während der Kernwerkstoff vor allem eine hohe Zähigkeit aufweist.
Vergütungsstahl: Die entsprechenden Eigenschaften werden hier durch eine geeignete Wärmebehandlung
erreicht. Dies kann in Form einer Vergütung erfolgen. Vergüten bedeutet eine Wärmebehandlung von Stahl
durch Abschrecken aus Härtetemperatur und Anlassen auf so hohe Temperatur, dass die Zähigkeit wesentlich
gesteigert wird. Gleichzeitig wird eine höhere Elastizitätsgrenze erreicht. Die Anlasstemperaturen liegen
zwischen 400 bis 700°C. Manche Stähle müssen nach dem Anlassen schnell abgekühlt werden (Anlassen:
Um notwendige Eigenschaften der Werkstücke, wie zum Beispiel gewünschte Festigkeit oder
Zähigkeit, zu erlangen, ist ein erneutes Erwärmen der Werkstücke auf bestimmte Temperaturen
notwendig.).
Stahl: Stahl wird am meisten für mittel- und hoch beanspruchte Zahnräder verwendet.
Stahlguss: Unter Stahlguss versteht man Eisenwerkstoffe mit C-Gehalten bis max. 2%, die in Formen aus Sand
zu Konstruktionsteilen vergossen werden. Infolge der höheren Schmelztemperatur ist Stahlguss gegenüber
Gusseisen schwer vergießbar. Stahlguss ist kostengünstiger als gewalzte oder geschmiedete
Räder.
Nitrierstahl: Bei diesem Stahl handelt es sich um Vergütungsstahl, der mit Cr, Mo und Ni legiert
ist.
Schwarzer Temperguss (perlitisches Gefüge): Teile mit komplizierter Form, die hohe Zähigkeit,
Schlagfestigkeit und gute Bearbeitung besitzen müssen, werden aus Temperguss hergestellt. Temperguss ist
für kleinere Abmessungen geeignet und besitzt gegenüber Stahlguss eine höhere Festig- und
Zähigkeit.
Gusseisen Kugelgraphit (perlitisches Gefüge, bainitisches Gefüge, ferritisches Gefüge): Unter Gusseisen
versteht man alle Eisen-Werkstoffe mit mehr als 2% C. Der maximale C-Gehalt liegt jedoch selten höher als
4.5%. Gusseisen ist ein sehr kostengünstiger Konstruktionswerkstoff, dessen Zähigkeit und Verformbarkeit
jedoch deutlich geringer sind als beispielsweise bei Stahl. Gusseisen mit Kugelgraphit ist für Teile mit höheren
Schwingbeanspruchungen geeignet.
Grauguss: Grauguss ist für komplizierte Radformen geeignet und dabei kostengünstig, leicht zerspanbar und
geräuschdämpfend. Die Tragfähigkeit ist gering.
Wenn Sie die Option „Eigene Eingabe“ auswählen, werden alle Eingabe- und Auswahlmöglichkeiten aktiviert und Sie können Ihren individuellen Werkstoff anlegen. Ihre Eingaben werden beim Speichern in eine Berechnungsdatei mitgespeichert. Wählen Sie allerdings im Modul einen anderen Werkstoff aus der Listbox aus, gehen Ihre definierten Angaben verloren. Diese müssen Sie anschließend erneut eingeben.
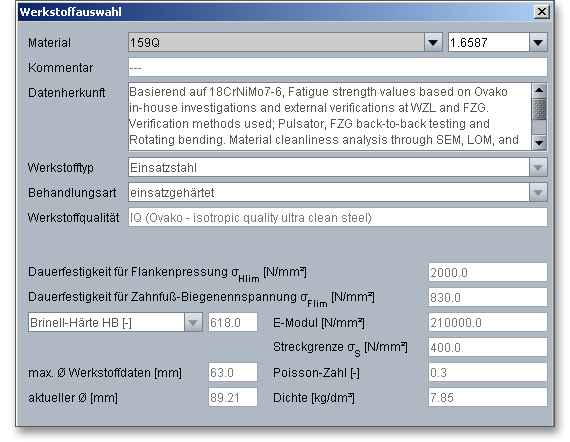
Aus der Listbox lassen sich die hochreinen Stähle 159X und 159Q von Ovako auswählen. Beide Stähle basieren auf dem Einsatzstahl 18CrNiMo7-6. Aufgrund deutlich geringerer Verunreinigungen weisen diese Stähle modifizierte Wöhlerkurven auf. D.h., im statischen Bereich sind beide Stähle vergleichbar mit dem 18CrNiMo7-6. Im Dauerfestigkeitsbereich bietet 159Q jedoch eine um ca. 30% höhere Leistungsfähigkeit für die Flankentragfähigkeit und um 60% höhere Festigkeit für die Zahnfußtragfähigkeit. Diese höheren Dauerfestigkeitswerte basieren auf internen Untersuchungen der Firma Ovako und wurden mit Untersuchungen am WZL in Aachen sowie am FZG in München bestätigt.
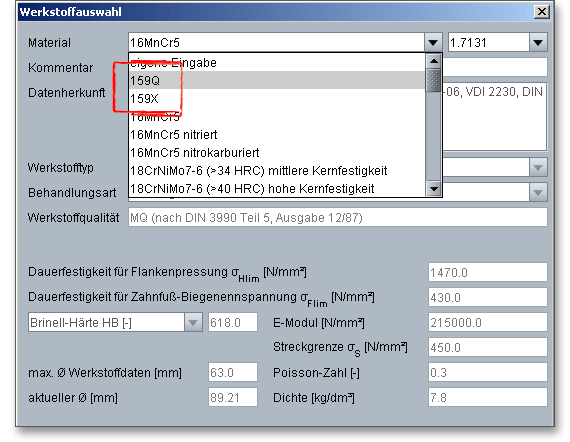
Der Stahl 159X weist eine etwas kleinere Leistungssteigerung gegenüber dem 18CrNiMo7-6 auf und eignet sich damit u.a. gut bei notwendiger Verbesserung bereits bestehender Konstruktionen. Das Potential des 159Q lässt sich besonders bei Neuauslegungen nutzen. Dabei kann es von Vorteil sein, den Fokus mit auf eine optimierte Fresstragfähigkeit zu legen. Diese lässt sich durch Vergrößerung der Zähnezahlen und gleichzeitiger Verkleinerung des Moduls erzielen. Dadurch ergeben sich in der Regel bessere Verzahnungswirkungsgrade und somit geringere Verlustleistungen. Diese Ovako-Stähle eröffnen komplett neue Möglichkeiten für Getriebe und besitzen ein hohes Potential zur weiteren Leistungssteigerung von Zahnradgetrieben und Verzahnungskomponenten.
Die Berechnung der Lastkollektive erfolgt nach DIN ISO 3990 Teil 6. Die Methode basiert auf der Palmgren-Miner-Regel. Für jeden einzelnen Lastfall werden die lastabhängigen K-Faktoren berechnet. Die Sicherheiten werden solange iteriert, bis sich die vorgeschriebene Schadenssumme bzw. der Schadenssummenbereich ergibt. Dieses Verfahren ist sehr genau und wird zum Beispiel in der Windkraftindustrie gefordert. Die Palmgren-Miner-Regel ist eine einfache lineare Schadenakkumulationstheorie. Diese Theorie geht davon aus, dass jede Belastungsstufe, die höher als die Dauerfestigkeit ist, zur Schädigung des Bauteils beiträgt.
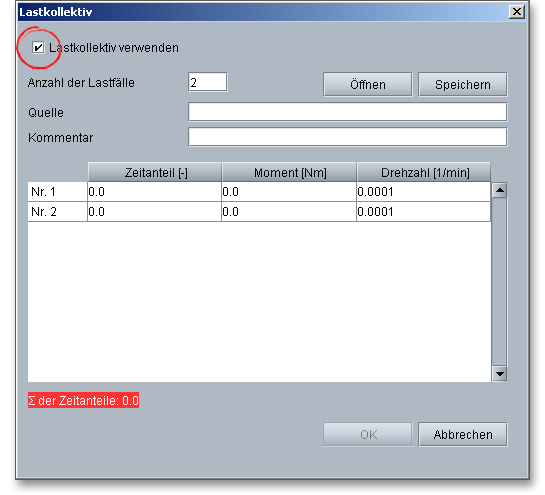
Klicken Sie auf den Button „Lastkollektiv“. Nach Aktivieren der Checkbox „Lastkollektiv verwenden“, lässt sich eine beliebige Anzahl an Lastkollektiven mit Häufigkeit, Moment und Drehzahl definieren. Die Lastkollektive werden dabei entweder direkt eingegeben oder lassen sich über eine Datei einlesen. Lastkollektive können gespeichert und geladen werden. Dazu nutzen Sie jeweils die beiden Buttons „Öffnen“ und „Speichern“.
Die von außen auf ein Getriebe einwirkenden dynamischen Zusatzkräfte werden durch den Anwendungsfaktor \(K_{A}\)bestimmt. Diese Zusatzkräfte sind abhängig von den Eigenschaften der treibenden und der getriebenen Maschine, den Kupplungen, den Massen- sowie den Betriebsverhältnissen. Da Fressen kein Ermüdungsschaden ist, soll der Anwendungsfaktor bei der Fresstragfähigkeitsberechnung den stärkeren Einfluss einzelner hoher Lastspitzen berücksichtigen. Einzelne Lastspitzen beeinflussen direkt nur die Flankentemperatur. Deshalb kann für die Berechnung der Fresstragfähigkeit der gleiche Anwendungsfaktor \(K_{A}\) wie für die Grübchen- und Zahnfußtragfähigkeit verwendet werden. Die nachfolgende Tabelle zeigt Anhaltswerte für den Anwendungsfaktor:
| Anwendungsfaktoren \(K_{A}\) nach DIN 3990-1: 1987-123
| ||||
| Arbeitsweise der | Arbeitsweise der getriebenen Maschine
| |||
| Antriebsmaschine | gleichmäßig | mäßige Stöße | mittlere Stöße | starke Stöße |
| (uniform) | (moderate) | (heavy) | ||
| gleichmäßig (uniform) | 1,0 | 1,25 | 1,5 | 1,75 |
| leichte Stöße | 1,1 | 1,35 | 1,6 | 1,85 |
| mäßige Stöße (moderate) | 1,25 | 1,5 | 1,75 | 2,0 |
| starke Stöße (heavy) | 1,5 | 1,75 | 2,0 | 2,25 oder höher |
| 3 Tabelle aus: DIN 3990 Teil 1, Dezember 1987, S. 55, Tab.: A1
| ||||
Hinweis: Neben dem Eingabefeld für den Anwendungsfaktor finden Sie einen Fragezeichen-Button. Klicken Sie dort, öffnet sich die obenstehende Tabelle. Einen solchen Fragezeichen-Button werden Sie noch häufiger neben verschiedenen Eingabefeldern finden.

Infolge von Herstellungsungenauigkeiten und elastischen Verformungen verteilt sich die Last nicht
gleichmäßig über die Zahnbreite. Die Auswirkungen der ungleichmäßige Lastverteilung über die
Zahnbreite gegenüber dem abweichungsfreien Zahneingriff berücksichtigen die Breitenfaktoren \(K_{H\beta }\) bei
Flankenpressung, \(K_{F\beta }\) bei Fußbeanspruchung und \(K_{B\beta }\) bei Fressen. Der Breitenfaktor für die Paarungen
Sonne-Planet und Planet-Hohlrad lässt sich individuell definieren oder nach DIN 3990 Teil 1 Methode C
berechnen.
Starten Sie das Modul, dann ist der Wert „1.25“ standardmäßig im Eingabefeld für die beiden Paarungen Sonne-Planet und Planet-Hohlrad definiert. Für den Fall, dass Sie bereits mit einem festgelegten Breitenfaktor arbeiten, können Sie diesen als Standard-Vorlage abspeichern. Somit öffnet sich das Berechnungsmodul dann mit Ihrem vorher definierten Breitenfaktor. Es besteht auch die Möglichkeit, sich den Breitenfaktor berechnen zu lassen. Klicken Sie dazu auf den den Taschenrechner-Button, um die Eingabemaske zur Auslegung des Breitenfaktors zu öffnen.
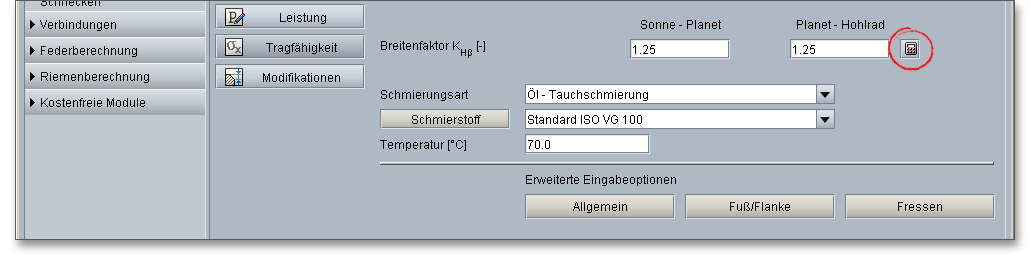
Wählen Sie aus der Listbox den Eintrag „DIN 3990 T1 Methode C“, um die Auswahlmöglichkeiten zu aktivieren. Der Breitenfaktor wird automatisch berechnet und kann mit dem Button „Übernahme“ anschließend in die Hauptmaske übernommen werden.
Lagerung des Planetenrades: Größere Planetenräder (bei Wälzlagern ungefähr ab i > 4) sind im
allgemeinen auf der im Planetenträger fest eingespannten Planetenachse drehbar gelagert, die freie
Biegelänge ist hierbei sehr klein. Bei kleineren Planeten (d.h. für kleinere Übersetzungen) kann man die
Lager meist nicht mehr im Radkörper unterbringen. Sie werden mit seitlich angedrehten Zapfen ausgeführt,
die beidseitig im Planetenträger drehbar gelagert sind.
Planetengetriebe mit oder ohne Flankenlinienkorrektur: Durch gezielte Abweichungen von der Evolvente (Zahnhöhenrichtung) und von der theoretischen Flankenlinie (Breitenrichtung) können die Auswirkungen von Herstellungsfehlern und elastischen Verformungen auf die Tragfähigkeit ausgeglichen werden. Breitenballigkeit und Endrücknahme gehören zu den wichtigsten Flankenkorrekturen und wirken sich günstig auf die Lastverteilung über der Zahnbreite aus. Durch die Breitenballigkeit oder mit einer Endrücknahme ausgeführte Verzahnungen kann die sich dadurch ergebene schiefe Lastverteilung abgebaut werden.
Reibung und Verschleiß an den Zahnflanken sollen durch den Schmierstoff verringert werden, denn die Zahnflankenreibung ist beispielsweise für Flankenabnutzung, Getriebeerwärmung sowie für das Getriebegeräusch verantwortlich. Eine verminderte Zahnflankenreibung verbessert den Wirkungsgrad, der allerdings noch von der Zahnbelastung, der Umfangsgeschwindigkeit, der Verzahnungsqualität und der Oberflächenbeschaffenheit der Zahnflanken abhängt. Soll ein Getriebe einwandfrei arbeiten, so hängt dies doch wesentlich vom gewählten Schmierstoff ab. Hier bietet sich ein flüssiger Schmierstoff an, der leicht zwischen die Zahnflanken gebracht werden kann. Ein Schmierstoff hat aber auch die Aufgabe, Reibungswärme abzuführen und Getriebeelemente so vor Korrosion zu schützen. Meist werden auch die zum Getriebe gehörigen Lager und Kupplungen mit dem Schmierstoff versorgt, der somit auch dafür geeignet sein muss.

Für die Wahl flüssiger Schmierstoffe gilt im Allgemeinen: „Je kleiner die Umfangsgeschwindigkeit und je
größer die Wälzpressung sowie die Rauigkeit der Zahnflanken sind, um so höher muss die Viskosität sein.
Eine höhere Viskosität bewirkt eine größere hydrodynamische Tragfähigkeit und Belastbarkeit, und
somit auch eine höhere Fresslastgrenze, bei der Riefenbildung oder Fressen der Zahnflanken
einsetzt.“ (Muhs/Wittel/Jannasch/Voßiek: Roloff/Matek Maschinenlemente, 17. überarbeitete Auflage, Vieweg
Verlag, Wiesbaden 2005)
Hinweis: Die Viskosität eines Schmiermittels sollte hoch sein, wenn das Getriebe wechselnden Belastungen
ausgesetzt ist, da dadurch auftretende Stöße gedämpft werden.
Im Gehäuse laufende Räder werden fast ausnahmslos mit Öl geschmiert. Hierbei unterscheidet man zwischen Tauch- und Einspritzschmierung. Bei Planetengetrieben wird das Öl meist von der Stegwelle aus den Zahneingriffen und Lagern zugeführt. Es kann durch Bohrungen im Zahngrund des Ritzels zu den Zahneingriffen befördert werden.
Wenn Sie auf den Button „Schmierstoff“ klicken, gelangen Sie in die umfangreiche Schmierstoffdatenbank.
Hier erhalten Sie detaillierte Informationen zu den Ölen und Fetten, wie zum Beispiel die Dichte, die Viskosität
oder die Kraftstufe des FZG-Tests. Wählen Sie aus der Listbox „eigene Eingabe“, so lässt sich auch hier ein
individueller Schmierstoff definieren.
Klicken Sie in der Hauptmaske der Tragfähigkeit auf den Button „Allgemein“ oder „Fuß/Flanke“, so werden die erweiterten Eingabeoptionen aufgerufen. Ändern Sie in der dann folgenden Maske keine Eingaben, so wird mit den Standard-Eingabewerten gerechnet.

Klicken Sie auf den jeweils aktiven Pfeil, um zwischen der Stirnradpaarung Sonne-Planet oder Planet-Hohlrad schnell hin und her zu wechseln.
Die Oberflächenrauigkeit der Flanken beeinflusst die Flankentragfähigkeit. Die gemittelte Rautiefe \(R_{z}\) ist das arithmetische Mittel aus den Einzelrautiefen fünf aneinandergrenzender Einzelmessstrecken. Die Eingabe der Rautiefe erfolgt für Sonne, Planet und Hohlrad am Fuß und an der Flanke. Die Öberflächenrauigkeit eines Werkstückes wird hinsichtlich der zu erfüllenden Funktion und nach der wirtschaftlichen Fertigung gewählt. Hohe Herstellkosten ergeben sich aus einer zu feinen Oberfläche. Eine zu grobe Oberfläche kann unter Umständen nicht die geforderte Funktionalität erfüllen.

Schleifkerben können die Dauerfestigkeit erheblich mindern, sogar so sehr, dass aus einer Schleifkerbe ein Zahnbruch entstehen kann.
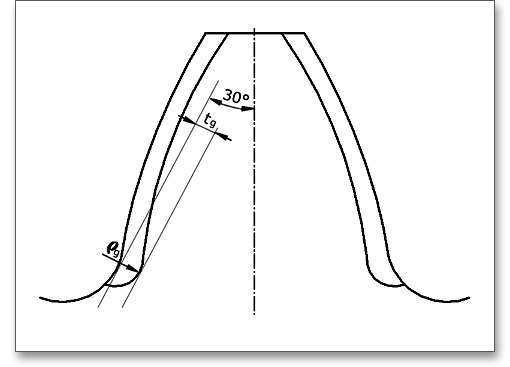
Durch Kugelstrahlen kann besonders die Dauerfestigkeit der durch Schleifkerben geschädigten Räder gesteigert werden. Ein sorgfältiges Ausschleifen der Kerben ist grundsätzlich ebenfalls geeignet. Mit einem Klick auf den Fragezeichen-Button, lässt sich die Abbildung für die Schleifkerbe öffnen.

Die Einhärtetiefe ist wesentlich für die Grübchentragfähigkeit und wird von der Einwärmtiefe (auf Härtetemperatur erwärmte Randschicht), der Einhärtbarkeit des Werkstoffes und der Wirkung des Abschreckverfahrens bestimmt. Die Einsatzstähle erhalten ihre kennzeichnenden Eigenschaften durch das Einsatzhärten. Dieses kombinierte Wärmebehandlungsverfahren besteht aus den folgenden Teilprozessen:

Hinweis: Die eAssistant-Software berechnet für Einsatzstähle automatisch die Einsatzhärtetiefe, es besteht
jedoch die Möglichkeit, diese auch individuell vorzugeben. Ist die individuelle Einsatzhärtetiefe kleiner als die
optimale Einsatzhärtetiefe, dann wird die Dauerfestigkeit entsprechend reduziert. Die Berechnung der
optimalen Einsatzhärtetiefe sowie die Reduzierung der Dauerfestigkeit bei verringerter Einsatzhärtetiefe
erfolgt nach: „Tobie, Thomas: Zur Grübchen- und Zahnfußtragfähigkeit einsatzgehärteter Zahnräder,
Dissertation Technische Universität München (Lehrstuhl für Maschinenelemente, Forschungsstelle für
Zahnräder und Getriebebau) 2001, Kap. 10.3: Eingliederung der Versuchsergebnisse in das Rechenverfahren
nach DIN 3990“.
Der Technologiefaktor \(Y_{T}\) berücksichtigt die Veränderung der Fußfestigkeit durch Bearbeitung.
\[\sigma _{Flim} = \sigma _{Flim0} Y_{T}\]
| \(\sigma _{Flim0}\) | Zahnfuß-Dauerfestigkeit aus Werkstoff-Kennwerten |
| \(\sigma _{Flim}\) | Zahnfuß-Dauerfestigkeit mit Einfluss des Technologiefaktors |
| \(Y_{T}\) | Technologiefaktor (siehe nachfolgende Tabelle) |
| Technologiefaktor \(Y_{T}\) nach Linke4
| |
| Art der Bearbeitung des Zahngrundes | Technologiefaktor \(Y_{T}\) |
| Kugelstrahlen: | 1,2 bis 1,4 |
| gilt für einsatzgehärtete oder carbonierte Verzahnung; in der verfestigten Schicht nicht geschliffen |
|
| Rollen: | 1,3 bis 1,5 |
| gilt für flamm- oder induktionsgehärtete Verzahnung; in der verfestigten Schicht nicht geschliffen |
|
| Schleifen: | allgemein: 0,7 |
| gilt für einsatzgehärtete oder carbonierte Verzahnung | bei CBN-Schleifscheiben: 1 |
| Spanende Bearbeitung: | 1 |
| gilt nicht für geschliffene Verzahnung |
|
| 4 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag München Wien, 2. Auflage 2010, S. 320, Tab.: 6.5/6
| |
Die Tabellen für den Technologiefaktor und den Betriebsartenfaktor lassen sich über den Fragezeichen-Button öffnen.

Die Zahnfuß-Dauerfestigkeit \(\sigma _{Flim}\) wird mit dem Einfluss der Betriebsart korrigiert.
\[\sigma _{Flim} = \sigma _{Flim0} Y_{A}\]
| \(\sigma _{Flim0}\) | Zahnfuß-Dauerfestigkeit aus Werkstoff-Kennwerten |
| \(\sigma _{Flim}\) | Zahnfuß-Dauerfestigkeit mit Einfluss des Betriebsartenfaktors |
| \(Y_{A}\) | Betriebsartenfaktor (siehe nachfolgende Tabelle) |
Für den Betriebsartenfaktor \(Y_{A}\) können die folgenden Anhaltswerte verwendet werden:
| Betriebsartenfaktor \(Y_{A}\) nach Linke5
| ||
| Betriebsart | Betriebsartenfaktor \(Y_{A}\) | Belastungsrichtung |
| schwellend | 1 | 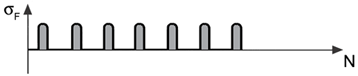 |
| wechselnd | 0,7 | 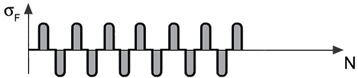 |
| reversierend | 0,85 - 0,15 \(\frac {lgN_{rev}}{6}\) (für \(1\leq N_{rev} \leq 10^{6}\)) 0,7 (für \(N_{rev} > 10^{6}\)) | 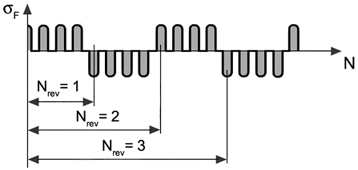 |
| Hinweis: \(N_{rev}\) = Anzahl der Lastrichtungsänderungen während der Betriebszeit
| ||
| 5 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag München Wien, 1996, S. 321, Tab.: 6.5/7
| ||
Hinweis: Für schwellende und wechselnde Beanspruchung gibt die DIN 3990 identische Werte
an.
Infolge von Flankenlinienabweichungen, Breitenballigkeit der Zahnflanken, Verformung der Zähne, des Gehäuses, der Wellen und der Radkörper sowie Schwingungen der Radmassen kommt es zu inneren dynamischen Zusatzkräften. Sie steigen mit der Umfangsgeschwindigkeit der Zahnkränze, nehmen aber mit steigender Belastung der Zähne ab. Der Dynamikfaktor \(K_{V}\) berücksichtigt diese inneren dynamischen Zusatzkräfte. Der Dynamikfaktor kann für die Paarungen Sonne-Planet und Planet-Hohlrad über das Schloss-Symbol manuell eingegeben werden.

Die Stirnfaktoren berücksichtigen die Auswirkung ungleichmäßiger Kraftaufteilung auf mehrere gleichzeitig im
Eingriff befindliche Zahnpaare (das heißt in Umfangsrichtung) auf die Flankenpressung (\(K_{H\alpha }\)), auf
die Fressbeanspruchung (\(K_{B\alpha }\)) und auf die Zahnfußbeanspruchung (\(K_{F\alpha }\)). Der Stirnfaktor kann für die
Paarungen Sonne-Planet und Planet-Hohlrad über das Schloss-Symbol individuell modifiziert
werden.
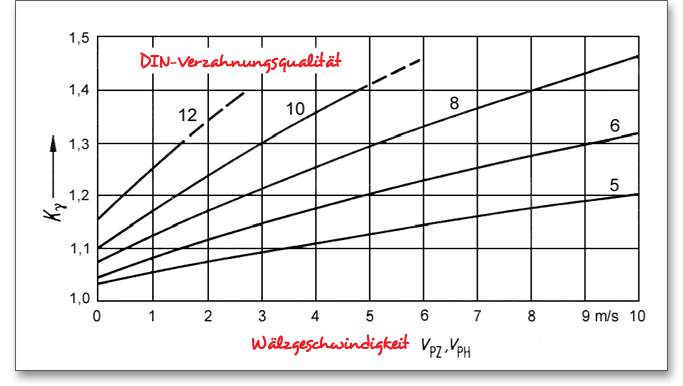
Erstrebenswert ist immer eine möglichst gleichmäßige Lastverteilung, um so die Vorteile von Planetengetrieben optimal zu nutzen. Flankenspiele und unvermeidbare Fertigungsabweichungen des Getriebes führen jedoch zu einer ungleichmäßigen Lastverteilung auf die einzelnen Planetenräder. Die Gesamtumfangskraft teilt sich also nicht ganz gleichmäßig auf die Zahneingriffe an den Planeten auf. Die Lastverteilung auf die Planetenräder wird bei der Tragfähigkeitsberechnung durch den Aufteilungsfaktor \(K_{\gamma }\) berücksichtigt. Die Lastverteilung auf die Planetenräder kann durch eine hohe Herstellungsqualität verbessert werden. Für Getriebe in der Schiffstechnik verlangt der Germanische Lloyd 2008 die folgenden Aufteilungsfaktoren:
| Aufteilungsfaktor
| ||||
| Anzahl der Planeten | bis zu drei Planeten | 4 Planeten | 5 Planeten | 6 Planeten |
| \(K_{\gamma }\) | 1,0 | 1,2 | 1,3 | 1,6 |
In Abhängigkeit der Verzahnungsqualität und der Wälzgeschwindigkeit werden auch im Niemann (Niemann, G.: Maschinenelemente Band II, Springer Verlag Berlin, 1989, S. 361, Abb. 22.5/2d) Werte vorgeschlagen.
Sind die Zahnbreiten von Ritzel und Rad ungleich, so ist je Zahnende höchstens ein Überstand von 1mal Normalmodul als mittragend anzunehmen. Bei randschichtgehärteten Zahnrädern sind ungehärtete Bereiche der Zahnbreite einschließlich der Übergangszone nur zu 50% als mittragend anzusehen. Wenn jedoch durch Breitenballigkeit oder Endrücknahme der Kontakt nicht bis zur Stirnseite reicht, ist für Ritzel und Rad die Breite des schmaleren von beiden einzusetzen. Der Wert für die mittragende Breite kann über den Schloss-Button individuell modifiziert werden.

In einzelnen Fällen kann die Bildung von Grübchen an der Zahnflanke zugelassen werden. Hier finden Sie die
Option „Grübchen zulassen“. Anfänglich auftretende, zum Stillstand kommende Grübchenbildung ist im
allgemeinen oft zulässig. Oft gehen insbesondere bei einsatzgehärteten oder nitrierten Verzahnungen von
Grübchen in Zahnfußnähe Ermüdungsbrüche aus, wodurch eine jeweils individuelle Beurteilung erforderlich
ist. In einigen Grenzfällen (Luft- und Raumfahrt) sind deshalb einzelne Grübchen absolut unzulässig. Auch
bei Turbogetrieben können Grübchen zu Schwingungen und zu erhöhten dynamischen Zusatzkräften
führen.
Auch für die Fresstragfähigkeit gibt es erweiterte Eingabeoptionen. Klicken Sie für diese Eingabeoptionen auf den Button „Fressen“.
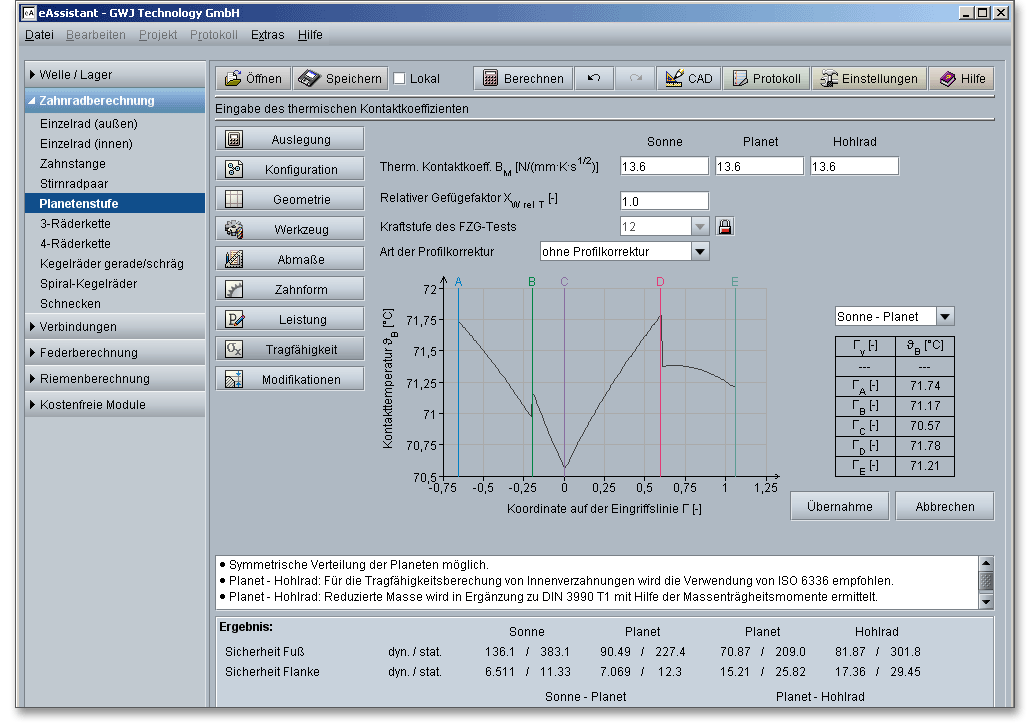
Der thermische Kontaktkoeffizient wird für die Ermittlung des Blitzfaktors benötigt. Durch den
Blitzfaktor wird der Einfluss der Werkstoffeigenschaften von Ritzel und Rad auf die Blitztemperatur
berücksichtigt.
Der relative Gefügefaktor \(X_{WrelT}\) berücksichtigt die Eigenschaften des Werkstoffes auf die Fressintegraltemperatur und wird bestimmt mit:
\[X_{WrelT} = \frac {X_{W}}{X_{WT}}\]
| \(X_{W}\) | Empirisch ermittelte Gefügefaktor ist aus der unteren Tabelle zu entnehmen |
| \(X_{WT}\) | Gefügefaktor für die Versuchszahnräder, die zur Ermittlung der Fresstemperatur verwendet werden. |
| Für den FZG-Zahnradtest ist \(X_{WT}\) = 1,0. |
| Werkstoff/Wärmebehandlung | Gefügefaktor \(X_{W}\) |
| vergütete Stähle | 1,00 |
| phosphatierte Stähle | 1,25 |
| verkupferte Stähle | 1,50 |
| bad-gasnitirierte Stähle | 1,50 |
| einsatzgehärtete Stähle | |
| - mit unterdurchschnittlichem Austenitgehalt | 1,15 |
| - mit normalem Austenitgehalt | 1,00 |
| - mit überdurchschnittlichem Austenitgehalt | 0,85 |
| austenitische Stähle (rostfreie Stähle) | 0,45 |
| 6 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung,
Carl Hanser Verlag München Wien, 2. Auflage 2010, S. 367, Tab.: 6.5/16
| |
Da das Fressen kein Ermüdungsschaden ist und durch Schmierstoffe beeinflusst wird, wird der maßgebende Tragfähigkeitskennwert des Schmierstoffes mit einem Zahnrad-Kurztest ermittelt. Mit diesem Test wird die Fresstragfähigkeit eines Schmierstoffes bei bestimmten Betriebsbedingungen untersucht. Dafür eignet sich der sogenannte FZG-Test (FZG - Forschungsstelle für Zahnräder und Getriebebau der Technischen Universität München). Dieser Test ist ein genormtes Prüfverfahren nach DIN 51354. Als Prüfelemente werden genormte, einsatzgehärtete und geschliffene Geradstirnräder mit starker einseitiger Profilverschiebung verwendet. In einer Zahnrad-Verspannungs-Prüfmaschine mit definierten technischen Daten wird die Beanspruchung stufenweise gesteigert. Insgesamt sind 12 Kraftstufen für die Prüfung vorgesehen und am Ende jeder Kraftstufe werden die Ritzelzahnflanken auf Oberfächenschäden untersucht. Schließlich wird die Kraftstufe ermittelt, in der der Verschleiß in eine Hochlage springt und die Zahnflanken fressen und so stärkere Schäden an der Zahnflanke auftreten. Nicht bei allen Schmierstoffen ist in der Schmierstoffdatenbank eine Kraftstufe für den FZG-Test definiert. Durch ein Klicken auf den Schloss-Button lässt sich die Listbox freischalten und eine Kraftstufe auswählen.
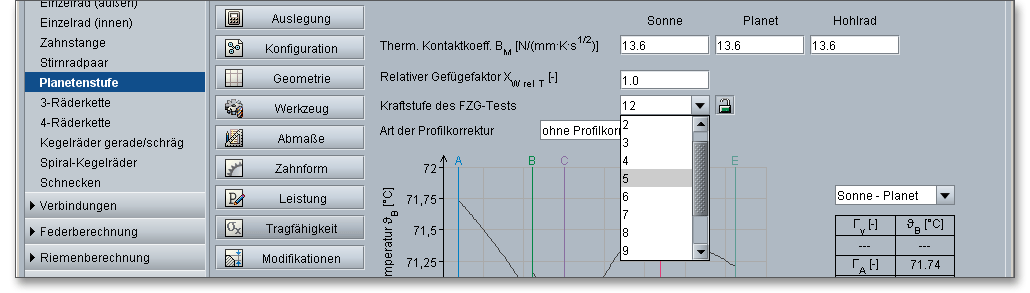
Bei Hochleistungsgetrieben können Korrekturen an der theoretischen Evolvente vorgenommen werden. Über die Listbox können Sie die Art der Profilkorrektur bestimmen. Unterschieden werden hierbei die folgenden Einträge: ohne Profilkorrektur, für Hochleistungsgetriebe, bei gleichmäßigem Eingriff.
Der Kraftaufteilungsfaktor \(X_{\Gamma }\) drückt den Einfluss der Kraftaufteilung auf einanderfolgende, im Eingriff stehende Zahnpaare aus. Der Verlauf des Kraftaufteilungsfaktors wird durch einen polygonartigen Verlauf über der Eingriffslinie dargestellt. Die Werte in den Punkten A und E hängen von der Form der Profilkorrekturen beider Zahnräder ab. Der Kraftaufteilungsfaktor ergibt sich nach DIN 3990 (siehe Teil 4, S. 17):
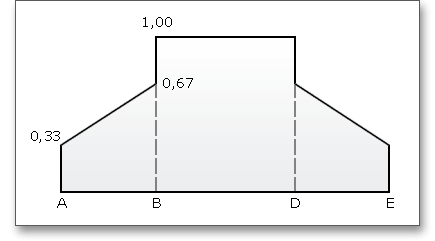
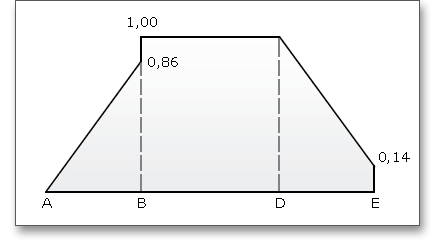
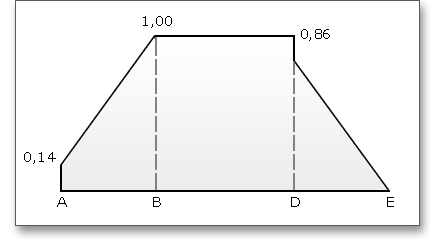
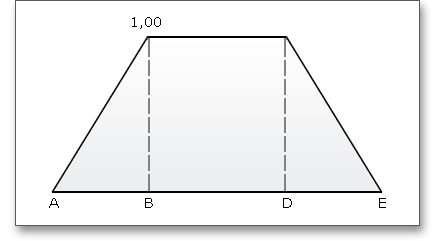
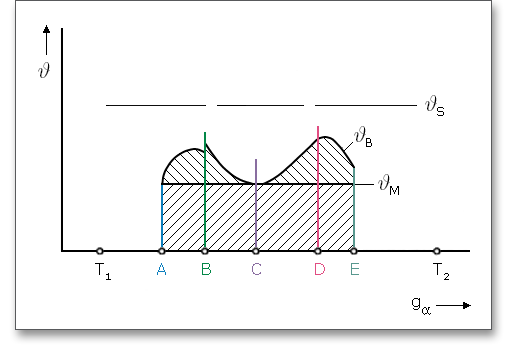
Die Kontakttemperatur besitzt entlang der Eingriffsstrecke unterschiedliche Werte aufgrund des Blitztemperatur-Verlaufes.
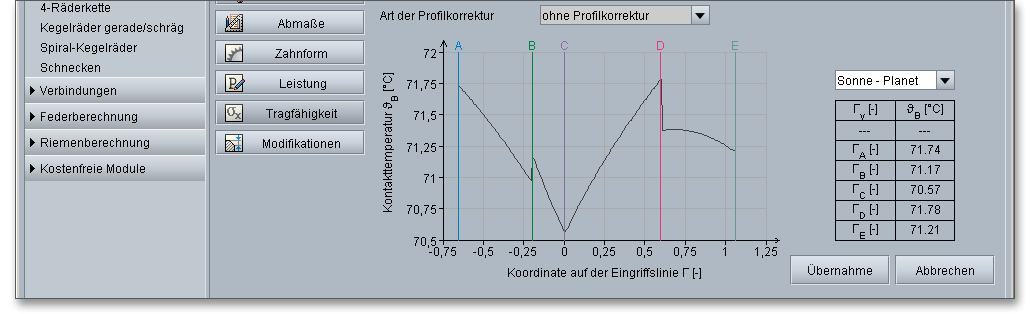
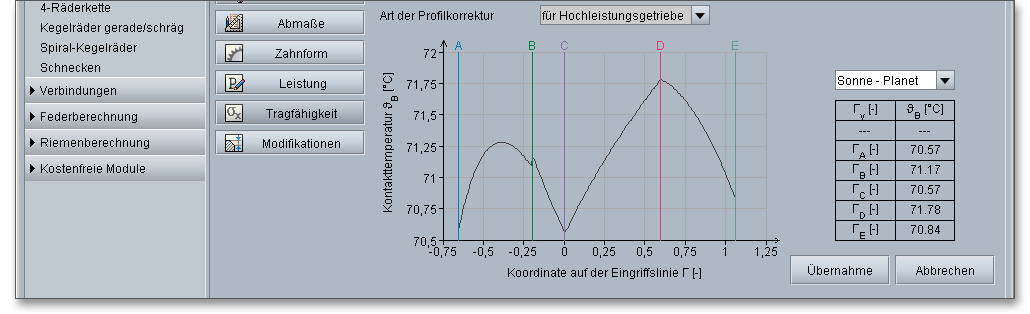
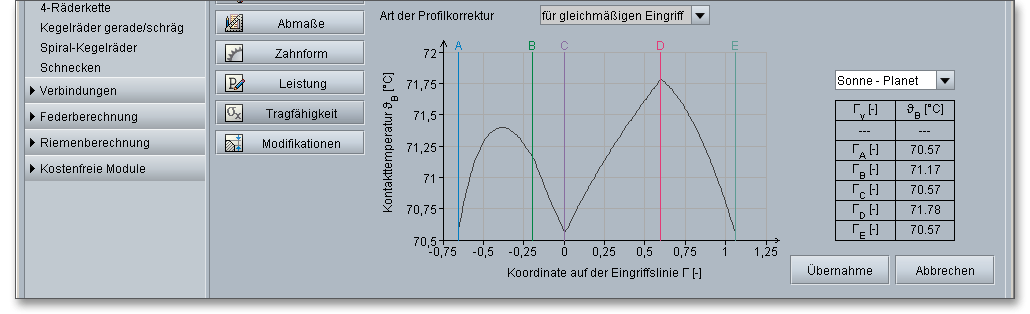
Hohe Oberflächentemperaturen, die durch hohe Belastungen und Gleitgeschwindigkeiten hervorgerufen werden, können zu einem Zusammenbruch des Schmierfilms führen. Aufgrund dessen werden in der DIN 3990 zwei Berechnungsverfahren aufgeführt, die auf unterschiedlichen Kriterien für die Schadensentwicklung basieren und im Berechnungsmodul Anwendung finden:
Warmfressen tritt nach dem Blitztemperatur-Verfahren dann auf, wenn die momentane Kontakttemperatur \(\vartheta _{B}\) hoch genug ist, um ein örtliches Verschweißen der sich berührenden Zahnflanken hervorzurufen. Die Kontakttemperatur \(\vartheta _{B}\) in einem beliebigen Berührpunkt \(Y\) ergibt sich aus der Summe der Massentemperatur \(\vartheta _{M}\) und der Blitztemperatur \(\vartheta _{fla}\) zu
\[\vartheta _{B} = \vartheta _{M} + \vartheta _{fla}\]
Nach dem Blitztemperatur-Verfahren tritt kein Fressen auf, solange die Kontakttemperatur \(\vartheta _{B}\) (als Summe der
Massentemperatur \(\vartheta _{M}\) und der Blitztemperatur \(\vartheta _{fla}\)) in allen Eingriffspunkten eine Fresstemperatur \(\vartheta _{S}\) nicht übersteigt.
Die Fresstemperatur \(\vartheta _{S}\) wird in Zahnradversuchen eines Werkstoff-Schmierstoff-Werkstoff-Systems ermittelt und
auf das betrachtete Zahnradpaar übertragen.
Hinweis: Die Buchstaben A bis E kennzeichnen die wichtigen Punkte von Eingriffsbeginn bis Eingriffsende.
Die Sicherheit \(S_{B}\) gegen Fressen bestimmt sich nach dem Blitztemperatur-Verfahren zu:
\[S_{B} = \frac {\vartheta _{S} - \vartheta _{oil}}{\vartheta _{Bmax} - \vartheta _{oil}} \geq S_{Bmin}\]
| \(\vartheta _{Bmax}\) | Maximalwert der Kontakttemperatur längs der Eingriffsstrecke |
| \(\vartheta _{oil}\) | Schmieröltemperatur vor dem Eingriff |
| \(\vartheta _{S}\) | Fresstemperatur |
Der Sicherheitsfaktor \(S_{Bmin}\) ist davon abhängig, ob das Getriebe erst nach einem guten Einlauf in Betrieb
genommen wird. Bei sorgfältigem Einlauf kann bis \(S_{Bmin} \approx 1\) kein Fressschaden auftreten. Ohne Einlauf ist bis \(S_{Bmin} \approx 3\) ein
Fressen ausgeschlossen.
Nach dem Kriterium des Integraltemperatur-Verfahren tritt Fressen gerade dann auf, wenn die Integraltemperatur einen bestimmten Wert, die sogenannte Fress-Integraltemperatur, überschreitet. Die Fress-Integraltemperatur wird als charakteristischer Wert für das System Werkstoff-Schmierstoff-Werkstoff eines Zahnradpaares angenommen, der in Zahnradversuchen ermittelt wird. Die Fresssicherheit nach dem Integral-Temperatur-Kriterium \(S_{intS}\) ergibt sich aus:
\[S_{intS} = \frac {\vartheta _{intS}}{\vartheta _{int}} \geq S_{Smin}\]
| \(\vartheta _{intS}\) | Fress-Integraltemperatur |
| \(\vartheta _{int}\) | Integraltemperatur |
Zur Vermeidung unnötiger Gefahren und zur Berücksichtigung von Ungenauigkeiten in der Berechnung, muss ein Fress-Sicherheitsfaktor für die Integraltemperatur eingeführt werden. In DIN 3990 werden aus praktischen Untersuchungen die folgenden Anhaltswerte gegeben:
| \(S_{intS} < 1,0\) | mit hoher Wahrscheinlichkeit ist mit dem Auftreten von Fressen zu rechnen |
| \(1,0 \leq S_{intS} \leq 2,0\) | bei sorgfältigem Einlauf der Getriebe, gutem Tragbild und realen Belastungsannahmen |
| sind keine Fressschäden zu erwarten |
| \(S_{intS} > 2,0\) | ein Fressen ist kaum zu befürchten |
Alternativ zur Tragfähigkeitsberechnung nach DIN 3390 Methode B können Sie über die Listbox auch die Berechnung für die Zahnfußfestigkeit und die Flanken- bzw. Grübchentragfähigkeit nach ISO 6336 Methode B (2006, 2019) auswählen. Alle Eingabefelder werden aktiviert.
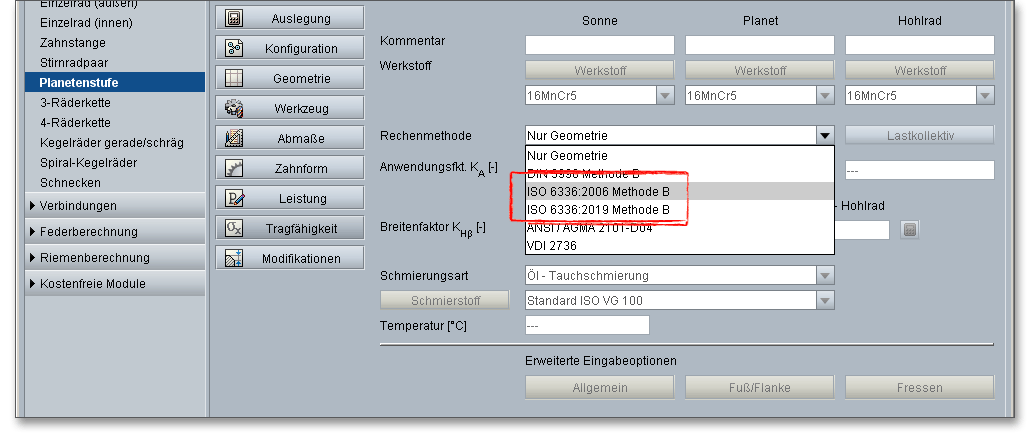
Die Festigkeitsberechnung nach ISO 6336 entspricht zum größten Teil der DIN 3990. Es gibt Faktoren, welche
die Zahnfußspannung und die Flankenfestigkeit beeinflussen, jedoch sind die Auswirkungen sehr gering und die
Sicherheiten unterscheiden sich kaum von der DIN 3990. Es gibt allerdings auch Faktoren, die einen
wesentlichen Einfluss auf die Sicherheiten haben. Dazu gehören zum Beispiel die Berechnung des
Schrägenfaktors \(Z_{\beta }\), die Berechnung der Lebensdauerfaktoren (\(Z_{NT}\) und \(Y_{NT}\)) für die Zahnfußfestigkeit sowie der
Übergang zur 60°-Tangente für Hohlräder.
Die Zahnfußtragfähigkeit wird mit dem Formfaktor berechnet, der den Einfluss der Zahnform auf die Biegenennspannung berücksichtigt. Zur Ermittlung des Formfaktors sind gemäß der DIN 3990 die Zahnfußdickensehne \(s_{Fn}\), der Biegehebelarm \(h_{Fe}\), der Kraftangriffswinkel im äußeren Einzeleingriffspunkt am Berührpunkt der 30°-Tangente zu berechnen. Bei Innenverzahnungen wird der Formfaktor als Näherung für eine Zahnstange berechnet und hat sich daher als sehr ungenau herausgestellt. Deshalb wird in der ISO 6336 für die Innenverzahnung ein größerer Tangentenwinkel von 60° für die Ermittlung des Berechnungsquerschnittes definiert. Durch das Anlegen der 60°-Tangente an die Fußkontur wird die Berechnung der Fußtragfähigkeit von Hohlrädern genauer bzw. realistischer und es ergeben sich so höhere Zahnfußsicherheiten.
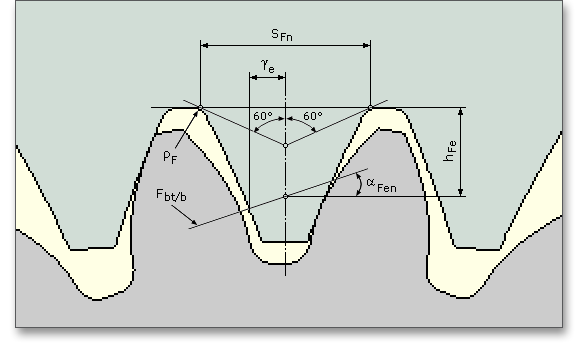
Der Lebensdauerfaktor \(Y_{NT}\) am Zahnfuß und der Lebensdauerfaktor \(Z_{NT}\) an der Flanke berücksichtigen die gegenüber der Dauerfestigkeit höhere Zahnflanken- und höhere Zahnfußtragfähigkeit bei einer begrenzten Anzahl von Lastwechseln. Die Faktoren werden hauptsächlich von Werkstoff, Wärmebehandlung, Anzahl der Lastwechsel sowie Kerbempfindlichkeit, Oberflächenbeschaffenheit und Baugröße beeinflusst. \(Z_{NT}\) und \(Y_{NT}\) lassen sich für die statische Festigkeit und die Dauerfestigkeit abhängig von Werkstoff und Wärmebehandlung aus der folgenden graphischen Abbildung entnehmen.
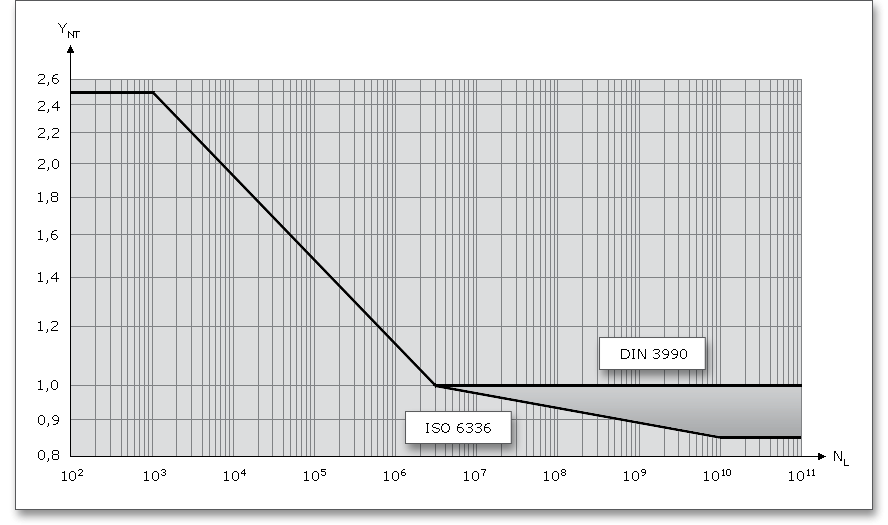
Lebendauerfaktor \(Y_{NT}\):
Für Lastwechselzahlen \(N_{L} = 3 \cdot 10^{6}\) kann bei optimalen Voraussetzungen von Werkstoff- und Herstellqualität mit \(Y_{NT}\) =
1,0 gerechnet werden. Im Bereich der statischen Beanspruchung \(N_{L} \leq 10^{3}\) wird der Lebensdauerfaktor zu
2,5.
Lebensdauerfaktor \(Z_{NT}\):
Für Lastwechselzahlen \(N_{L} = 5 \cdot 10^7\) kann bei optimalen Voraussetzungen von Werkstoff- und Herstellqualität mit \(Z_{NT}\) =
1,0 gerechnet werden. Im Bereich der statischen Beanspruchung \(N_{L} \leq 10^{5}\) wird der Lebensdauerfaktor zu
1,6.
Bei der Berechnung des Lebensdauerfaktoren \(Z_{NT}\) bzw. \(Y_{NT}\) treten wesentliche Unterschiede zwischen DIN 3990 und ISO 6336 auf. Einer der wichtigsten Unterschiede besteht beim Ansatz der vereinfachten Wöhlerlinie. Der Lebensdauerfaktor für die Zahnfußfestigkeit wird beim Erreichen der Lastwechselzahl für Dauerfestigkeit zu 1.0 (je nach Werkstoffart, üblicherweise bei \(3 \cdot 10^6\) Lastwechseln). Bei der DIN 3990 bleibt dieser Faktor bei höheren Lastwechselzahlen konstant, während sich bei der ISO 6336 eine Verminderung bis auf 0.85 bei \(10^{10}\) Lastwechseln ergibt. Erst danach, also bei \(10^{10}\) Lastwechseln, bleibt der Faktor konstant bei 0.85. Dieser Unterschied hat bei Berechnungen von Zahnrädern im Dauerfestigkeitsbereich nach ISO 6336 Sicherheiten zur Folge, die etwa um 15% niedriger sind als nach DIN 3990. Dieses gilt auch für den Lebensdauerfaktor für die Flankenpressung. Die Faktoren lassen sich über den Schloss-Button individuell modifizieren. Klicken Sie auf den Schloss-Button, dann werden die Eingabefelder aktiviert und die Lebensdauerfaktoren können angepasst werden. Denken Sie daran, den Schloss-Button geöffnet zu lassen, sonst werden die ursprünglichen Standardwerte wieder eingesetzt.
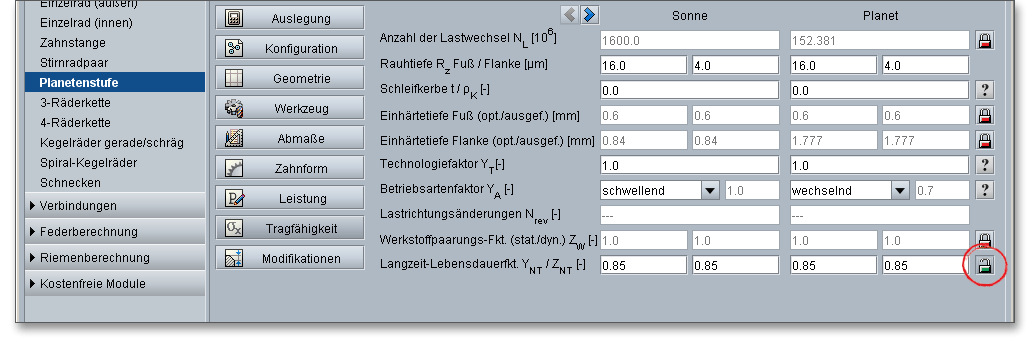
Ein weiterer Unterschied zwischen DIN und ISO stellt die Ermittlung der Eingriffsfedersteifigkeit \(c_{\gamma }\) für die
Berechnung des Breitenlastfaktors dar. Der Faktor \(K_{H\beta }\) dient der Berücksichtigung der Lastverteilung über
die Zahnflankenbreite. In der neuen ISO 6336 wird für die Berechnung von \(K_{H\beta }\) mit einer um 15%
reduzierten Eingriffsfedersteifigkeit \(c_{\gamma }\) im Vergleich zur DIN 3990 gearbeitet. Dies führt zu leicht geringeren
Breitenfaktoren.
Um die bei dünnen Radkränzen, wie z.B. bei Planeten- oder Hohlrädern, zusätzlich auftretende Belastung im Zahnfuß zu berücksichtigen, wurde der Zahnkranzdickenfaktor \(Y_{B}\) neu eingeführt. Bei Außenverzahnungen wird die Erhöhung der Zahnfußspannung durch geringe Zahnkranzdicke auf die Zahnhöhe und bei Innenverzahnungen auf den Normalmodul bezogen berücksichtigt. Eine Abminderung der Tragfähigkeit ergibt sich für Außenverzahnungen bei einer Zahnkranzdicke \(s_{R} < 1,2 \cdot h_{t}\) bzw. rund \(2,8 \cdot m_{n}\), für Innenverzahnungen bei Zahnkranzdicken \(s_{R} < 3,5 \cdot m_{n}\) (ISO 6336 Edition 2006 - Was ist neu?: Dr.-Ing. R. Heß, Dipl.-Ing. B. Kisters, A. Friedr. Flender AG, Bocholt, Tagungsbeitrag Dresdener Maschinenelemente Kolloquium 2009).
Ein weiterer Unterschied betrifft den Schrägenfaktor. Der Schrägenfaktor \(Z_{\beta }\) berücksichtigt den Einfluss des Schrägungswinkels auf die Grübchentragfähigkeit, wobei Einflüsse wie die Kraftverteilung entlang der Berührlinien beachtet werden. \(Z_{\beta }\) hängt nur vom Schrägungswinkel \(\beta \) ab. In DIN und ISO ist die Formel zur Berechnung des Schrägenfaktors unterschiedlich. Die DIN gibt die folgende Gleichung zur Berechnung des Schrägenfaktors an (wobei \(\beta \) der Schrägungswinkel am Teilzylinder ist):
\[Z_{\beta } = \sqrt {\cos \beta }\]
Die ISO 6336 verwendet dagegen die folgende Gleichung:
\[Z_{\beta } = \frac {1}{\sqrt {\cos \beta }}\]
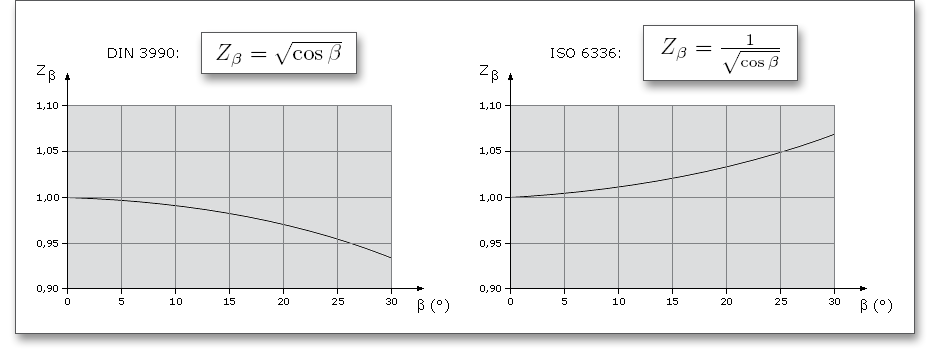
In der neuesten Ausgabe der ISO 6336 wurde der Werkstoffpaarungsfaktor \(Z_{W}\) überarbeitet. Dieser Faktor dient
zur Berechnung der zulässigen Hertz´schen Pressung und somit zur Ermittlung der Flankentragfähigkeit und
wird für die Tragfähigkeitssteigerung bei unterschiedlich harten Verzahnungen genutzt. In der DIN 3990 und
der früheren Ausgabe der ISO 6336 war dieser Faktor lediglich abhängig von der Oberflächenhärte des
weicheren Zahnrades.
Der Einfluss der Oberflächenrauheit in die Berechnung des Werkstoffpaarungsfaktors wurde zusätzlich
integriert. Örtliche Flankenkrümmung, Umfangsgeschwindigkeit und Viskosität fließen dabei mit in die
Berechnung ein. Das bedeutet, dass der Werkstoffpaarungsfaktor bei rauerer Oberfläche des
härteren Zahnrades reduziert wird. Dies resultiert aus der Erkenntnis, dass eine raue Oberfläche
des härteren Zahnrades auch zum Verschleiß des weicheren Zahnrades führen kann. Dieser
Verschleiß stellt jedoch kein Schadenskriterium in der ISO 6336 dar. Deshalb wird die Untergrenze des
Werkstoffpaarungsfaktors \(Z_{W}\) auf 1,0 festgelegt (ISO 6336 Edition 2006 - Was ist neu?: Dr.-Ing. R. Heß, Dipl.-Ing.
B. Kisters, A. Friedr. Flender AG, Bocholt, Tagungsbeitrag Dresdener Maschinenelemente Kolloquium
2009).
In der ISO 6336 wird keine Berechnungsmethode für das Fressen vorgegeben. Bei der ISO/TR 13989 handelt es sich um einen Technical Report (Erstausgabe März 2000), also noch keine endgültige ISO-Norm. Da es jedoch im Moment keine verbindliche Norm gibt, empfiehlt sich daher die Anwendung der ISO/TR 13989. Sobald als Tragfähigkeitsmethode die ISO 6336 Methode B gewählt wird, erfolgt die Berechnung der Fresstragfähigkeit nach dem Blitz- als auch nach dem Integraltemperaturkriterium gemäß der ISO/TR 13989 Teil 1 (Blitztemperatur-Verfahren) und Teil 2 (Integraltemperatur-Verfahren).
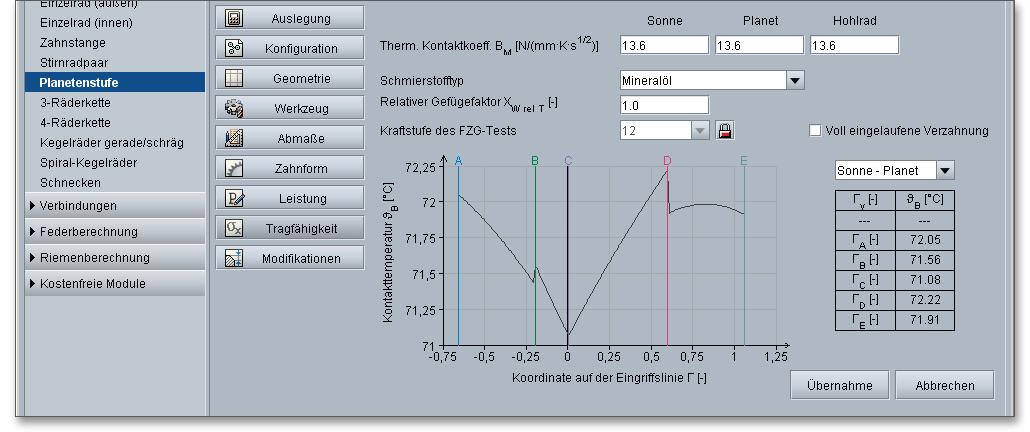
Der thermische Kontaktkoeffizient wird für die Ermittlung des Blitzfaktors benötigt. Durch den
Blitzfaktor wird der Einfluss der Werkstoffeigenschaften von Ritzel und Rad auf die Blitztemperatur
berücksichtigt.
Der Schmierstofffaktor \(X_{L}\) variiert in Abhängigkeit vom Schmierstofftyp. Aus der Listbox können die folgenden Schmierstofftypen ausgewählt werden:
| \(X_{L}\)= 1,0 | für Mineralöl |
| \(X_{L}\)= 0,6 | für Wasserlösliches Polyglykol |
| \(X_{L}\)= 0,7 | für nicht wasserlösliches Polyglykol |
| \(X_{L}\)= 0,8 | für Polyalphaolefin |
| \(X_{L}\)= 1,3 | für Phosphat-Ester |
| \(X_{L}\)= 1,5 | für Reibradöl |
Der relative Gefügefaktor \(X_{WrelT}\) berücksichtigt die Eigenschaften des Werkstoffes auf die Fress-Integraltemperatur und wird bestimmt mit:
\[X_{WrelT} = \frac {X_{W}}{X_{WT}}\]
| \(X_{W}\) | Empirisch ermittelte Gefügefaktor ist aus der unteren Tabelle zu entnehmen |
| \(X_{WT}\) | Gefügefaktor für die Versuchszahnräder, die zur Ermittlung der Fresstemperatur verwendet werden. |
| Für den FZG-Zahnradtest ist \(X_{WT}\) = 1,0. |
| Werkstoff | Gefügefaktor \(X_{W}\) |
| vergütete Stähle | 1,00 |
| phosphatierte Stähle | 1,25 |
| verkupferte Stähle | 1,50 |
| bad-gasnitirierte Stähle | 1,50 |
| einsatzgehärtete Stähle | |
| - mit unterdurchschnittlichem Austenitgehalt | 1,15 |
| - mit normalem Austenitgehalt | 1,00 |
| - mit überdurchschnittlichem Austenitgehalt | 0,85 |
| austenitische Stähle (rostfreie Stähle) | 0,45 |
| 7 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung,
Carl Hanser Verlag München Wien, 2. Auflage 2010, S. 367, Tab.: 6.5/16
| |
Da das Fressen kein Ermüdungsschaden ist und durch Schmierstoffe beeinflusst wird, wird der maßgebende Tragfähigkeitskennwert des Schmierstoffes mit einem Zahnrad-Kurztest ermittelt. Mit diesem Test wird die Fresstragfähigkeit eines Schmierstoffes bei bestimmten Betriebsbedingungen untersucht. Dafür eignet sich der sogenannte FZG-Test (FZG - Forschungsstelle für Zahnräder und Getriebebau der Technischen Universität München). Dieser Test ist ein genormtes Prüfverfahren nach DIN 51354. Als Prüfelemente werden genormte, einsatzgehärtete und geschliffene Geradstirnräder mit starker einseitiger Profilverschiebung verwendet. In einer Zahnrad-Verspannungs-Prüfmaschine mit definierten technischen Daten wird die Beanspruchung stufenweise gesteigert. Insgesamt sind 12 Kraftstufen für die Prüfung vorgesehen und am Ende jeder Kraftstufe werden die Ritzelzahnflanken auf Oberfächenschäden untersucht. Schließlich wird die Kraftstufe ermittelt, in der der Verschleiß in eine Hochlage springt und die Zahnflanken fressen und so stärkere Schäden an der Zahnflanke auftreten. Nicht bei allen Schmierstoffen ist in der Schmierstoffdatenbank eine Kraftstufe für den FZG-Test definiert. Durch ein Klicken auf den Schloss-Button lässt sich die Listbox freischalten und eine Kraftstufe auswählen.

Hohe Oberflächentemperaturen, die durch hohe Belastungen und Gleitgeschwindigkeiten hervorgerufen werden, können zu einem Zusammenbruch des Schmierfilms führen. Aufgrund dessen werden in der DIN 3990 zwei Berechnungsverfahren aufgeführt, die auf unterschiedlichen Kriterien für die Schadensentwicklung basieren und im Berechnungsmodul Anwendung finden:
Warmfressen tritt nach dem Blitztemperatur-Verfahren dann auf, wenn die momentane Kontakttemperatur \(\vartheta _{B}\) hoch genug ist, um ein örtliches Verschweißen der sich berührenden Zahnflanken hervorzurufen. Die Kontakttemperatur \(\vartheta _{B}\) in einem beliebigen Berührpunkt \(Y\) ergibt sich aus der Summe der Massentemperatur \(\vartheta _{M}\) und der Blitztemperatur \(\vartheta _{fla}\) zu
\[\vartheta _{B} = \vartheta _{M} + \vartheta _{fla}\]
Nach dem Blitztemperatur-Verfahren tritt kein Fressen auf, solange die Kontakttemperatur \(\vartheta _{B}\) (als Summe der Massentemperatur \(\vartheta _{M}\) und der Blitztemperatur \(\vartheta _{fla}\)) in allen Eingriffspunkten eine Fresstemperatur \(\vartheta _{S}\) nicht übersteigt. Die Fresstemperatur \(\vartheta _{S}\) wird in Zahnradversuchen eines Werkstoff-Schmierstoff-Werkstoff-Systems ermittelt und auf das betrachtete Zahnradpaar übertragen.
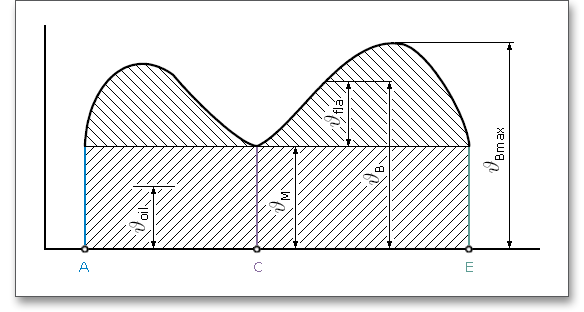
Die Sicherheit \(S_{B}\) gegen Fressen bestimmt sich nach dem Blitztemperatur-Verfahren zu:
\[S_{B} = \frac {\vartheta _{S} - \vartheta _{oil}}{\vartheta _{Bmax} - \vartheta _{oil}}\]
| \(\vartheta _{Bmax}\) | Maximalwert der Kontakttemperatur längs der Eingriffsstrecke |
| \(\vartheta _{oil}\) | Schmieröltemperatur |
| \(\vartheta _{S}\) | Fresstemperatur |
Der Sicherheitsfaktor \(S_{Bmin}\) ist davon abhängig, ob das Getriebe erst nach einem guten Einlauf in Betrieb
genommen wird. Bei sorgfältigem Einlauf kann bis \(S_{Bmin} \approx 1\) kein Fressschaden auftreten. Ohne Einlauf ist bis \(S_{Bmin} \approx 3\) ein
Fressen ausgeschlossen.
Nach dem Kriterium des Integraltemperatur-Verfahren tritt Fressen gerade dann auf, wenn die Integraltemperatur einen bestimmten Wert, die sogenannte Fress-Integraltemperatur, überschreitet. Die Fress-Integraltemperatur wird als charakteristischer Wert für das System Werkstoff-Schmierstoff-Werkstoff eines Zahnradpaares angenommen, der in Zahnradversuchen ermittelt wird. Die Fresssicherheit nach dem Integral-Temperatur-Kriterium \(S_{intS}\) ergibt sich aus:
\[S_{intS} = \frac {\vartheta _{intS}}{\vartheta _{int}} \geq S_{Smin}\]
| \(\vartheta _{intS}\) | Fress-Integraltemperatur |
| \(\vartheta _{int}\) | Integraltemperatur |
Zur Vermeidung unnötiger Gefahren und zur Berücksichtigung von Ungenauigkeiten in der Berechnung, muss ein Fress-Sicherheitsfaktor für die Integraltemperatur eingeführt werden. In der ISO/TR 13989-2 werden aus praktischen Untersuchungen die folgenden Anhaltswerte empfohlen:
| \(S_{intS} < 1,0\) | mit hoher Wahrscheinlichkeit ist mit dem Auftreten von Fressen zu rechnen |
| \(1,0 \leq S_{intS} \leq 2,0\) | bei sorgfältigem Einlauf der Getriebe, gutem Tragbild und realen Belastungsannahmen |
| sind keine Fressschäden zu erwarten |
| \(S_{intS} > 2,0\) | ein Fressen ist kaum zu befürchten |
Die Norm ANSI/AGMA 2101-D04 sieht die Berechnung von Sicherheiten für Fuß und Flanke vor. Darüber hinaus ist auch eine Berechnung des Fressrisikos möglich. Zusätzlich zu den Normen DIN 3990 und ISO 6336 bietet die ANSI/AGMA 2101-D04 auch die Berechnung von Verschleiß. Die eAssistantSoftware berechnet den Verschleiß als Ausfallwahrscheinlichkeit. Wählen Sie ANSI/AGMA 2101-D04 aus der Listbox und die Eingabefelder werden aktiviert. Im Folgenden werden einige Faktoren aus der Norm erläutert.
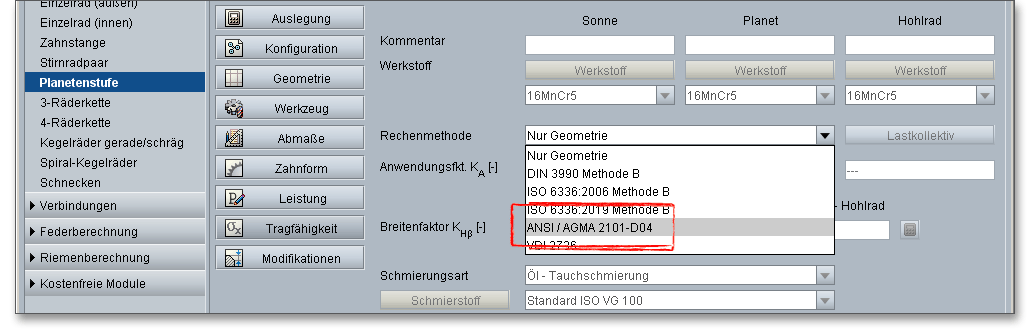
Mit der neuen Ausgabe der ANSI/AGMA 2101-D04 (ANSI/AGMA 2001-D04 Imperial Unit Edition) wurde der
Anwendungsfaktor aus der ANSI/AGMA 2101-C95 durch den Überlastfaktor \(K_{O}\) ersetzt.
Der Überlastfaktor soll alle von außen aufgebrachten Lasten berücksichtigen, die über die tangentiale
Nennlast \(F_{t}\) für eine bestimmte Anwendung hinausgehen. Überlastfaktoren können nur dann festgelegt werden,
wenn in einer bestimmten Anwendung umfangreiche Erfahrungen gesammelt wurden.
Bei einem Überlastfaktor von 1 beinhaltet diese Bemessungsmethode die Fähigkeit, eine begrenzte Anzahl
von bis zu 200 % kurzen Überlastzyklen auszuhalten (normalerweise weniger als vier Starts innerhalb von 8
Stunden, wobei die Spitze nicht länger als eine Sekunde dauert). Höhere oder häufigere kurzzeitige
Überlastungen sind gesondert zu berücksichtigen.
Bei der Bestimmung des Überlastfaktors \(K_{O}\) sollte die Tatsache berücksichtigt werden, dass viele Antriebsmaschinen und angetriebene Geräte einzeln oder in Kombination kurzzeitige Spitzendrehmomente entwickeln, die deutlich über den durch die Nennwerte der Antriebsmaschine oder des angetriebenen Geräts bestimmten Werten liegen. Es gibt viele mögliche Überlastungsquellen, die berücksichtigt werden sollten. Einige davon sind: Systemvibrationen, Beschleunigungsmomente, Überdrehzahlen, Schwankungen im Systembetrieb, Lastverteilung auf mehrere Antriebsmaschinen und Änderungen der Prozesslastbedingungen.
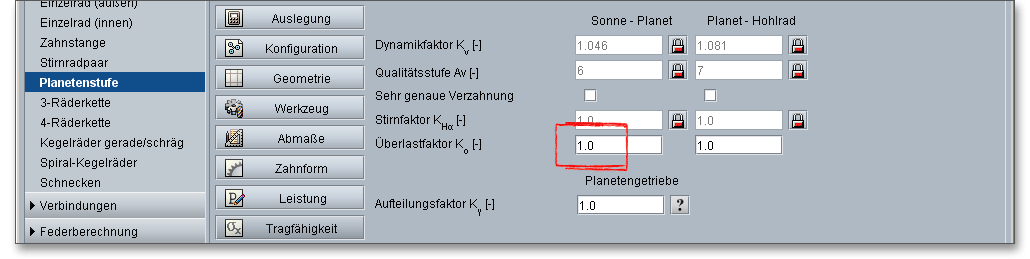
Die Lebensdauerfaktoren, \(Z_{N}\) und \(Y_{N}\), passen die zulässigen Dauerfestigkeitskennwerte für die erforderliche Anzahl
an Lastzyklen an. Für die Zwecke dieser Norm wird \(n_{L}\), die Anzahl der Lastwechsel, als die Anzahl der
Eingriffskontakte des untersuchten Zahns unter Last definiert.
Die zulässigen Dauerfestigkeitskennwerte der AGMA sind für \(10^{7}\) unidirektionale Lastwechsel bei 99 %
Zuverlässigkeit festgelegt. Der Lebensdauerfaktor passt die zulässigen Dauerfestigkeitskennwerte für eine
andere Lebensdauer als die \(10^{7}\) Zyklen an. Der Lebensdauerfaktor berücksichtigt die Wöhlerkurve
(S-N-Charakteristik) des Zahnradwerkstoffs sowie die allmählich zunehmende Zahnspannung, die durch
Zahnverschleiß auftreten kann, was wiederum zu erhöhten dynamischen Effekten führt, und durch
sich verschiebende Lastverteilungen, die während der Lebensdauer der Verzahnung auftreten
können.
Für Fälle, in denen sich die Oberflächenbeschaffenheit nachteilig auswirkt, wurden noch keine
Standardfaktoren für die Oberflächenbeschaffenheit von Verzahnungen festgelegt. In solchen Fällen sollte
ein Oberflächenfaktor verwendet werden, der größer als 1 ist. Der Oberflächenfaktor kann als 1
angenommen werden, sofern die geeignete Oberflächenbeschaffenheit erreicht wird.
Der Größenfaktor \(K_{S}\) spiegelt die Ungleichmäßigkeit der Werkstoffeigenschaften wider. Er hängt in erster Linie
ab von: Zahngröße, Teiledurchmesser, Verhältnis zwischen Zahngröße und Teiledurchmesser, Zahnbreite,
Fläche des Spannungsbilds, Verhältnis zwischen Einsatzhärtetiefe und Zahngröße, Härtbarkeit und
Wärmebehandlung der Werkstoffe. Für Fälle, in denen ein nachteiliger Größeneffekt auftritt, wurden noch
keine Standard-Größenfaktoren für Verzahnungen festgelegt. In solchen Fällen sollte ein Größenfaktor
verwendet werden, der größer als 1 ist. Der Größenfaktor kann für die meisten Zahnräder als 1
angenommen werden, vorausgesetzt, dass der Stahl für die Größe des Teils und die Wärmebehandlung und
das Härteverfahren richtig gewählt wurde.
Der Temperaturfaktor \(Y_{\vartheta }\) wird im Allgemeinen als 1 angenommen, wenn Getriebe bei Temperaturen des Öls oder des Rohlings arbeiten, die 120°C nicht überschreiten. Wenn die Betriebstemperaturen zu Temperaturen des Zahnradrohlings unter 0°C führen, ist besondere Vorsicht geboten. Bei Betriebstemperaturen von über 120°C wird \(Y_{\vartheta }\) mit einem Wert größer als 1,0 angesetzt, um den Einfluss der Temperatur auf den Ölfilm und die Materialeigenschaften zu berücksichtigen. Bei einigen Werkstoffen ist der Härte- und Festigkeitsverlust durch die Anlasswirkung von Temperaturen über 150°C zu berücksichtigen.
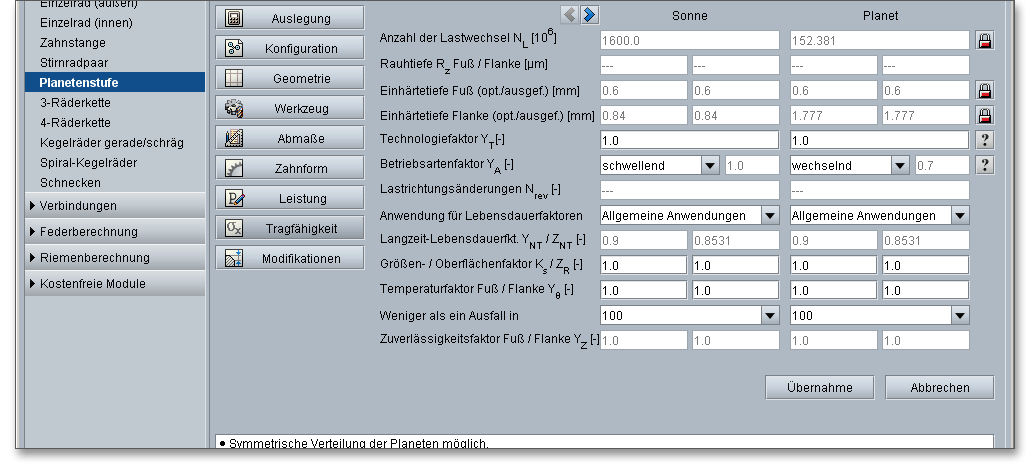
Der Zuverlässigkeitsfaktor \(Y_{Z}\) berücksichtigt die Auswirkung der normalen statistischen Verteilung von Fehlern, die bei der Materialprüfung festgestellt werden. Die in ANSI/AGMA (Tabellen 3 bis 6) angegebenen zulässigen Spannungen basieren auf einer statistischen Wahrscheinlichkeit von einem Ausfall von 100 bei \(10^{7}\) Zyklen. Die folgende Tabelle enthält Zuverlässigkeitsfaktoren, die zur Änderung dieser zulässigen Spannungen verwendet werden können, um diese Wahrscheinlichkeit zu ändern. Diese Zahlen basieren auf Daten, die von der U.S. Navy für den Ausfall durch Biegungversagen und Grübchenbildung entwickelt wurden. Andere Werte können verwendet werden, wenn spezifische Daten verfügbar sind.
| Zuverlässigkeitsfaktor \(Y_{Z}\) 110
| |
| Requirements of Application | \(Y_{Z}\) |
| Weniger als ein Ausfall von 10 000 | 1.50 |
| Weniger als ein Ausfall von 1000 | 1.25 |
| Weniger als ein Ausfall von 100 | 1.00 |
| Weniger als ein Ausfall von 10 | 0.852 |
| Weniger als ein Ausfall von 2 | 0.7023 |
| Anmerkungen: 1) Zahnbruch wird manchmal als größere Gefahr angesehen
als die Grübchenbildung. In solchen Fällen wird für die Biegung ein
größerer Wert für \(Y_{Z}\) gewählt. 2) Bei diesem Wert kann es eher zu plastischem
Fließen als zur Grübchenbildung kommen. 3) Aus der Extrapolation von
Testdaten.
| |
| 10 Tabelle aus: ANSI/AGMA 2001–D04: Fundamental Rating Factors and
Calculation Methods for Involute Spur and Helical Gear Teeth, 2016, S. 38,
Tab.: 11
| |
Der Servicefaktor \(C_{SF}\) wurde in früheren AGMA-Normen verwendet, um die kombinierten Auswirkungen von
Überlastung, Zuverlässigkeit, Lebensdauer und anderen anwendungsbezogenen Faktoren zu
berücksichtigen. Diese Norm bietet die Möglichkeit, Lastschwankungen (mit Überlastfaktor), statistische
Schwankungen (mit Zuverlässigkeitsfaktor) der Wöhlerdaten (S-N-Daten) sowie die Anzahl der Lastzyklen
(mit Lebensdauerfaktoren) zu berücksichtigen.
Der AGMA-Servicefaktor, wie er traditionell bei in Getriebeanwendungen verwendet wird, hängt von den
Erfahrungen ab, die bei jeder spezifischen Anwendung gesammelt wurden. Produktanwendungen können
dabei eine gute Quelle für einen geeigneten Wert des Servicefaktors sein. Die Gleichungen 28 und 29 der
AGMA 2101-D04 werden verwendet, um Nennleistungen für einen einheitlichen Servicefaktor festzulegen, auf
die die festgelegten Servicefaktoren unter Verwendung der Gleichung 30 angewendet werden können. In
diesem Fall wird der Lebensdauerfaktor anhand der Anzahl an Lastzyklen berechnet, die einer bestimmten
Anzahl von Stunden bei einer einer bestimmten Drehzahl entsprechen, um die Nennleistung für einheitliche
Servicefaktoren zu ermitteln.
Wenn besondere Erfahrungen und eine zufriedenstellende Leistung durch die erfolgreiche Anwendung
etablierter Servicefaktoren nachgewiesen wurden, können Werte für \(Z_{N}\) und \(Y_{N}\) von 1,0 angemessen
sein.
Für Zahnräder aus Kunststoff lässt sich die Tragfähigkeit nach VDI 2736 berechnen. Wählen Sie die VDI 2736 aus der Listbox. Alle Eingabefelder werden aktiviert. Die Tragfähigkeitsberechnung von Stirnrädern aus Thermoplasten lehnt sich an die für metallische Werkstoffe geltende DIN 3990 an. An Kunststoffzahnrädern können die gleichen Schäden wie an Stahlzahnrädern auftreten: Grübchen, Verschleiß oder Zahnbruch.
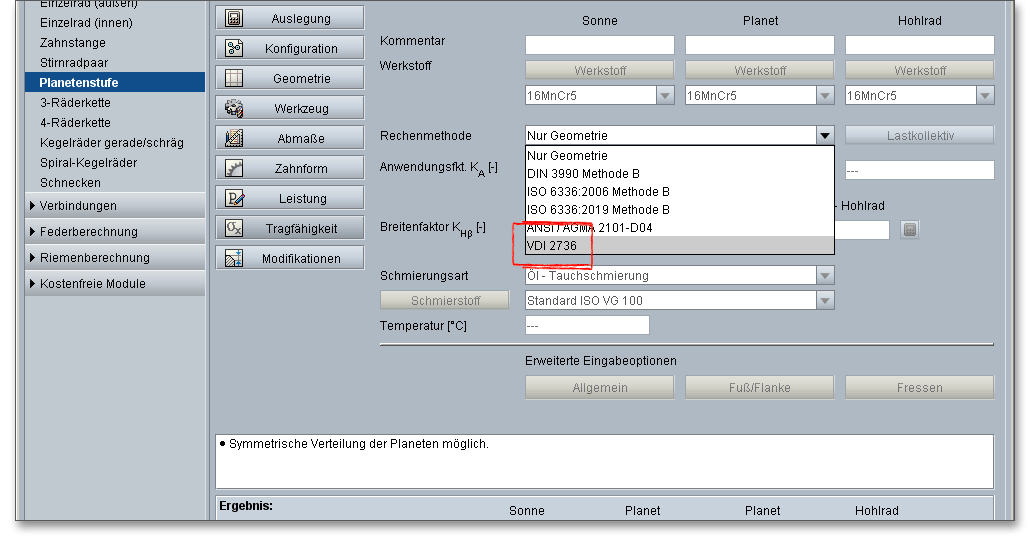
Thermoplaste weisen im Vergleich zu Metallen einige Besonderheiten auf, z.B.
Positive Eigenschaften gegenüber Stahlzahnrädern:
Zahnräder aus Kunststoff werden besonders dort eingesetzt, wo es auf geräuscharmen Lauf ankommt, da
Kunststoffe schwingungsdämpfend wirken. Sie kommen überwiegend für Geräte der Feinwerktechnik, für
Textil- und Haushaltsmaschinen in Betracht.
Es wird empfohlen, die Tragfähigkeit für Kunststoffzahnräder nach VDI 2736 zu berechnen. Es besteht im
eAssistant allerdings auch die Möglichkeit, mit der DIN 3990, ISO 6336 und ANSI/AGMA 2101-D04 die
Tragfähigkeit zu berechnen. Bei der Nachrechnung der Zahnfußtragfähigkeit nach VDI 2736 wird von der
Zahnfußspannung bei Kraftangriff am Zahnkopf und von der Annahme reiner Biegebeanspruchung
ausgegangen. Bei der DIN 3990 Methode B erfolgt der Kraftangriff am äußeren Einzeleingriffspunkt und die
Berechnung ist hier wesentlich genauer. In der VDI 2736 wird an einigen Stellen alternativ auf die DIN 3990
verwiesen. Wenn auf die DIN 3990 verwiesen wird, dann erfolgt die Berechnung der Tragfähigkeit im
eAssistant nach dieser Norm.
Die Kunststoffe sind in der allgemeinen Werkstoffdatenbank hinterlegt. Für diese Werkstoffe wurden die temperaturabhängigen Kennwerte, wie Zeitfestigkeiten und E-Modul, detailliert aus den zur Verfügung stehenden Diagrammen der VDI 2736 approximiert und entsprechend hinterlegt. Diese werden genutzt, um mit den nach der VDI 2736 automatisch berechneten Zahnfuß- und Flankentemperaturen die zugehörigen Materialkennwerte für die Tragfähigkeitsberechnung zu ermitteln. Überschreiten die berechneten Zahnflanken- oder Zahnfußtemperaturen die maximalen Gebrauchstemperaturen der jeweiligen Kunststoffe, so erhalten Sie im Meldungsfenster einen entsprechenden Warnhinweis. Bei der Berechnung der Tragfähigkeit nach DIN 3990, ISO 6336 und ANSI/AGMA 2101-D04 werden die Werkstoffkennwerte auf Basis der Schmierstofftemperatur gewählt.
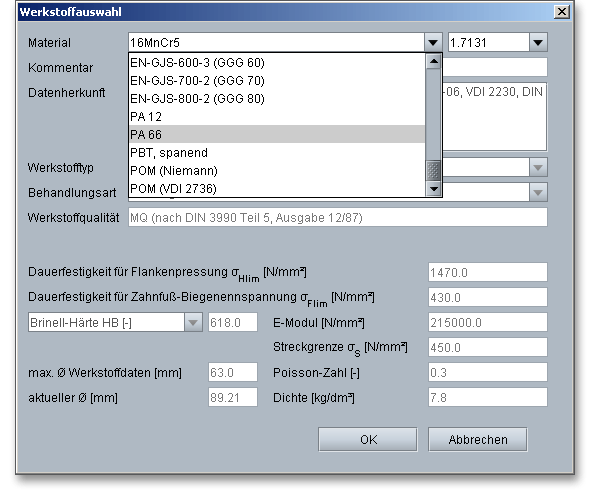
Hinweis: PA- und POM-Räder haben eine höhere Tragfähigkeit und bessere Wärmeabführung bei
Paarung mit einem Metallrad. Möglichst nie gleiche Kunststoffe paaren. Das Geräuschverhalten bei der
Paarung von Thermoplastzahnrädern ist günstiger als bei Kunststoff/Metall.
Für die Berechnung der Zahnflanken- und Zahnfußtemperaturen können alternativ zu einer automatischen
Vorbelegung die Gehäusebauform, die wärmeabführende Oberfläche sowie der Wärmeübergang und
Wärmewiderstand vorgegeben werden.
Als Materialpaarungen sind sowohl Paarungen von Kunststoff/Kunststoff als auch von Kunststoff/Metall möglich. Darüber hinaus werden auch Paarungen von Metall/Metall, für eine Vergleichsmöglichkeit zu den Berechnungsmethoden für metallische Zahnräder, unterstützt. Die Lastkollektivberechnung ist ebenfalls für die Tragfähigkeitsberechnung nach VDI 2736 verfügbar. Kunststoffzahnräder werden häufig bei Trockenlauf betrieben. Aus der Listbox für die „Schmierungsart“ lässt sich die Option „Trockenlauf“ auswählen.

Herstellungs- und Einbauungenauigkeiten sowie Verlagerungen der Räder unter Last führen dazu, dass die Zähne nicht auf ihrer ganzen Breite voll zum Tragen kommen. Bei größeren Verlagerungen besteht sogar die Gefahr des Kantentragens. Um die Auswirkungen der Herstellfehler und die belastungsbedingten Verformungen auf die Lastverteilung zu minimieren sowie die Laufeigenschaften zu verbessern und Laufgeräusche zu mindern, werden gewollte Abweichungen von der theoretischen Form in Zahnhöhenrichtung und von der theoretischen Flankenlinie in Breitenrichtung ausgeführt.
Es gibt verschiedene Arten von Zahnkorrekturen. Kurze und lange lineare oder kurze und lange
kreisförmige Kopf- und Fußrücknahmen sind typische Profilmodifikationen. Breitenballigkeit und
Endrücknahme gehören zu den wichtigsten Flankenlinienkorrekturen und wirken sich günstig auf die
Lastverteilung über der Zahnbreite aus. Durch Breitenballigkeit oder Endrücknahme kann eine
schiefe Lastverteilung abgebaut werden. Voraussetzung für die Anwendung von Modifikationen ist
eine DIN-Qualität von 7 oder feiner, da Profilkorrekturen nur bei einer Mindestgenauigkeit sinnvoll
sind.
Bei einer Profilmodifikation werden die Flanken teilweise hinter die Evolvente zurückgenommen.
Bei der Kopfrücknahme und Fußrücknahme wird das Flankenprofil am Zahnkopf bzw. am Zahnfuß durch eine zusätzliche Werkstoffabtragung verändert. Das erzeugte veränderte Flankenprofil geht möglichst stetig in das theoretische Flankenprofil über. Werden Zahnkopf und Zahnfuß gleichzeitig zurückgelegt, dann ergibt sich daraus die Höhenballigkeit.
Die einfachste Korrektur ist die Kopfrücknahme an Rad und Ritzel. Man kann aber statt an beiden Rädern
auch nur ein Rad mit einer Kopf- und Fußrücknahme ausführen. Aus der Listbox können Sie für die Kopf-
und Fußrücknahme die Formen lineare sowie kreisförmige Rücknahme auswählen. Die lineare
Rücknahme hat den größten Materialabtrag zur Folge und somit die größte Entlastung im wirksamen
Flankenbereich.
Bei der Festlegung der Längen der Profilkorrektur unterscheidet man zwischen kurzer und langer Profilkorrektur. Bei langer Kopf- und Fußrücknahme ist das gesamte Doppeleingriffsgebiet korrigiert, während bei kurzer Ausführung nur die Hälfte des Doppeleingriffsgebiets zurückgenommen ist. Es werden entweder lange oder kurze Rücknahmen auf einer Verzahnung realisiert. Für möglichst geräuscharme Getriebe ist meistens die lange Profilkorrektur geeignet, die kurze Profilkorrektur hat ein besseres Lastverhalten. Sofern die Sprungüberdeckung ausreicht, ist eine lange Profilkorrektur eher für eine Schrägverzahnung geeignet.

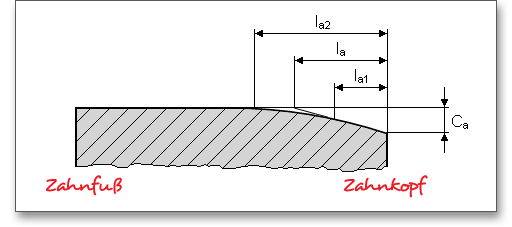
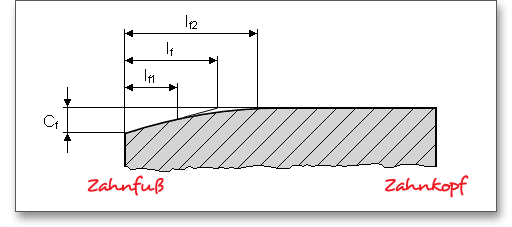
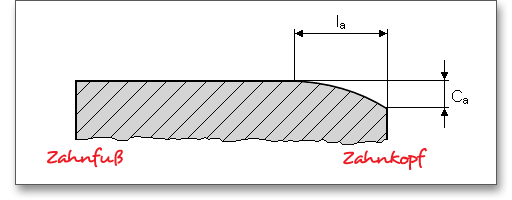
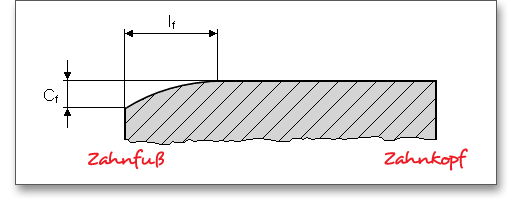
Die lineare Kopf- und Fußrücknahme wird im eAssistant mit einer Übergangsrundung vom korrigierten zum unkorrigierten Bereich ausgeführt. In die entsprechenden Eingabefeldern können Sie den Beginn sowie das Ende der Übergangsrundung eingeben. Bei der kreisförmigen Rücknahme entfällt die Eingabe des Übergangsbereichs.

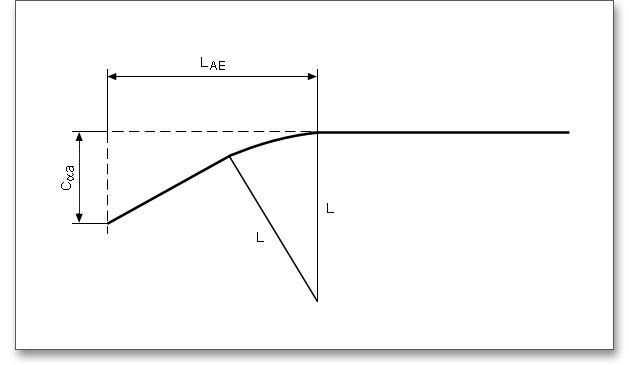
Mit dem %-Button lässt sich die Leistung bzw. das Drehmoment enstellen, die für die Auslegung des Kopfrücknahmebetrages verwendet werden soll. Bei Kenntnis der Betriebsbedingungen kann der Leistungsanteil entsprechend festgelegt werden. Mit einem Klick auf den Taschenrechner-Button wird dann der Betrag \(C_{a}\) der Kopfrücknahme für Rad 1 und Rad 2 berechnet. Ist die Länge der Profilkorrektur bekannt, dann können Sie diesen Wert einfach in das Eingabefeld eintragen. Ist der Wert nicht bekannt, wählen Sie aus der Listbox „kurz“ oder „lang“ und die eAssistant-Software bestimmt automatisch die Länge der Profilkorrektur. Haben Sie zum Beispiel nur einen Durchmesser auf einer Zeichnung gegeben, ist es auch möglich, einen Durchmesser zu definieren. Klicken Sie auf den „d/l“-Button auf der rechten Seite, um zwischen der Eingabe der Rücknahme als Durchmesser oder als Länge umzuschalten.
Aktivieren Sie die Checkbox „Theoretische Eingriffsstrecke verwenden“ wird die theoretische Eingriffsstrecke des Zahnrades mit einer Zahnstange genutzt.
Kopfrücknahme und Fußrücknahme (gemeinsam angewandt) ergeben die Höhenballigkeit. Verglichen zum theoretischen Profil werden Zahnkopf und Zahnfuß zurückgenommen.
Die Höhenballigkeit kann als symmetrische Balligkeit aus der Listbox ausgewählt werden, anschließend können Sie für \(C_{ha}\) einen Wert in das Eingabefeld ergänzen.
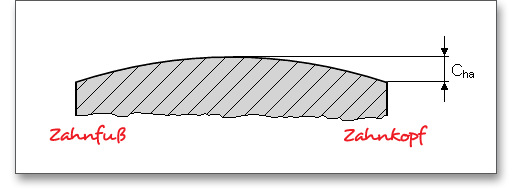
Bei Breitenkorrekturen handelt es sich um gewollte Abweichungen von der Flankenlinie. Wenn Breitenballigkeit und Endrücknahme sinnvoll gewählt werden, dann wirken sich beide sehr günstig auf die Lastverteilung aus.
Bei der Endrücknahme wird die Zahndicke an einem Zahnende gemindert, dadurch lässt sich eine Überlastung des jeweiligen Zahnendes minimieren. Eine Endrücknahme empfiehlt sich nur dann, wenn Balligschleifen oder -schaben nicht möglich sind. Im Allgemeinen wird die Rücknahme für beide Zahnenden gleich groß gewählt.
Die Endrücknahme kann beidseitig, links oder rechts ausgeführt werden.

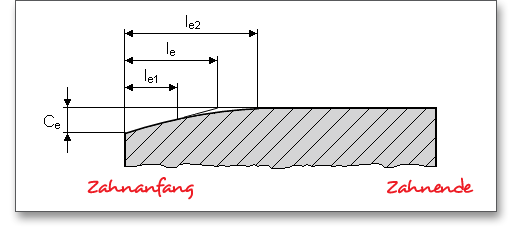
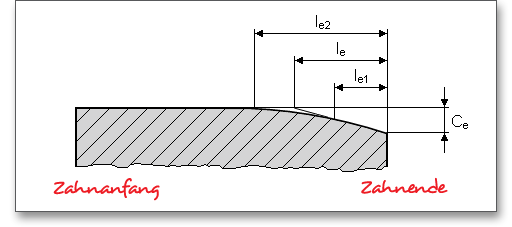
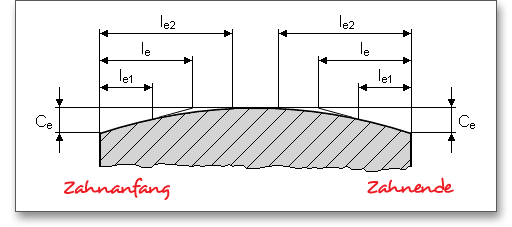
Nach DIN 3990 Teil 1 berechnet sich die Höhe der Endrücknahme wie folgt:
Für vergütete Räder: \(C_{e} \approx F_{\beta xcv}\) zuzüglich einer Herstelltoleranz von 5 bis 10 \(\mu m\). Entsprechend der Festlegung für \(F_{\beta xcv}\) (ursprünglich wirksame Flankenlinienabweichung im Betrieb) in DIN 3990 soll \(C_{e}\) betragen:
\[C_{e} = f_{sh} + 1,5 \cdot f_{H\beta }\]
Für randschichtgehärtete und nitrierte Räder: \(C_{e} \approx 0,5 \cdot F_{\beta x cv}\) zuzüglich einer Herstelltoleranz von 5 bis
10 \(\mu m\). \(C_{e}\) soll damit ungefähr betragen:
\[C_{e} = 0,5 \cdot (f_{sh} + 1,5 \cdot f_{H\beta })\]
Für sehr steife Konstruktionen, bei denen \(f_{sh}\) nahezu vernachlässigt werden kann oder wo die Verformung im Mittel durch eine Flankenlinien-Winkelkorrektur ausgeglichen wird, darf man ansetzen:
\[C_{e} = f_{H\beta }\]
Für sehr genaue und betriebssichere Räder mit hohen Umfangsgeschwindigkeiten reichen 60 bis 70% der oben angegebenen Werte.
Nach DIN 3990 Teil 1 berechnet sich die Breite der Endrücknahme wie folgt:
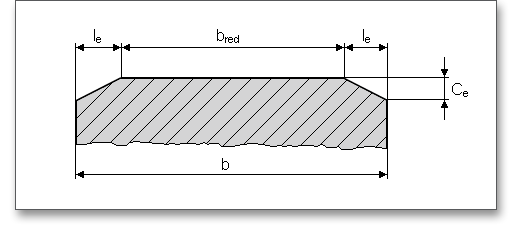
Bei ungefähr gleichbleibender Belastung und höheren Umfangsgeschwindigkeiten:
\(l_{e}\)= kleinerer Wert von \(0,1 \cdot b\) oder \(1 \cdot m\)
Bei unterschiedlichen Belastungen, kleinen und mittleren Geschwindigkeiten wählt man:
\[b_{red} = (0,5\ bis\ 0,7) \cdot b\]
Man benutzt diese Art von Flankenkorrektur, um Herstellabweichungen und Verformungen der Zahnräder unter Last auszugleichen und insbesondere die Zahnenden zu entlasten und ein Kantentragen bei unterschiedlichen Betriebsbelastungen zu vermeiden.
Die Balligkeit wird üblicherweise symmetrisch zur Mitte der Verzahnungsbreite oder asymmetrisch ausgeführt. Bei der Breitenballigkeit weicht die Zahnflanke von ihrer theoretischen Form in Richtung der Zahnbreite ab, so dass die Flankenlinie zum Zahninneren hin gekrümmt ist. Sie können zwischen symmetrischer und asymmetrischer Breitenballigkeit wählen.
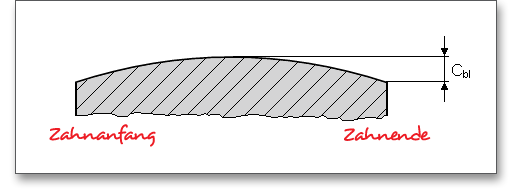
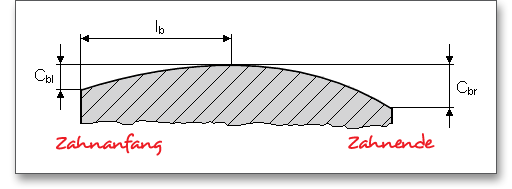
Nach DIN 3990 Teil 1 berechnet sich die Höhe der Breitenballigkeit wie folgt:
\[C_{b} = 0,5 \cdot (f_{sh} + 1,5 \cdot f_{H\beta })\]
Für sehr steife Konstruktionen, bei denen \(f_{sh}\) nahezu vernachlässigt werden kann oder wo die Verformung im Mittel durch eine Flankenlinien-Winkelkorrektur ausgeglichen wird, darf man ansetzen:
\[C_{b} = f_{H\beta }\]
Für sehr genaue und sicher ausgelegte Räder mit hohen Umfangsgeschwindigkeiten reichen 60 bis 70% der oben angegebenen Werte aus, wobei \(10 \leq C_{b} \leq 25\ \mu m\) sein soll, zuzüglich einer Herstelltoleranz von ungefähr 5 \(\mu m\).
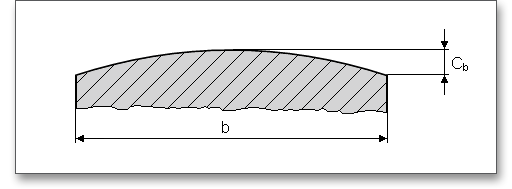
Laut DIN 3990 wird die Flankenlinienabweichung \(f_{sh}\) ohne Berücksichtigung der Balligkeit bestimmt. Das
bedeutet, dass in der Tragfähigkeitsberechnung auf der Untermaske vom \(K_{H\beta }\) „keine Korrektur“ gesetzt werden
muss. Hinsichtlich des nach DIN 3990 berechneten Vorschlagswertes der Breitenballigkeit handelt es sich
immer um einen Wert bezogen auf die wirksame Summe der Modifikationen von Ritzel und Rad im Eingriffsfeld.
Das bedeutet, die Modifikationen können nur an einem Rad oder auf die Paarung aufgeteilt ausgeführt
werden. Deshalb liefert die Vorschlagswertberechnung für Rad 1 und 2 immer erst einmal den
gleichen Wert. Wie dieser berechnete Wert dann gegebenenfalls aufgeteilt wird, entscheidet der
Anwender.
Lässt man sich zunächst für Rad 1 den Wert vorschlagen, kann man diesen dann auf Rad 1 und Rad 2 aufteilen. Dies gilt auch für Rad 2. Bei einer Aufteilung des Balligkeitsbetrages auf beide Räder gibt es verschiedene Aufteilungsverhältnisse. Häufig nutzt man hier den Ansatz:
\[C_{b}^{2} = C_{b1}^{2} + C_{b2}^{2}\]
Deshalb wird immer nur der Wert für die Paarung als Vorschlagswert über den Taschenrechner-Button generiert.
Bei der Auslegung eines Planetengetriebes ist es wichtig, auf mögliche Eingriffsstörungen zu achten und so zum Beispiel erhöhte Laufgeräusche oder Schäden, wie Zahnbruch oder Verschleiß zu vermeiden. Eingriffsstörungen können bei der Außenverzahnung des Planetengetriebes am Zahnfuß des Ritzels auftreten und so zu einem Verklemmen von Ritzel und Rad führen. Diese Störungen treten vorallem bei sehr großen positiven Profilverschiebungen auf. Der Eingriff bei Innenradpaarungen gestaltet sich schwieriger als bei Außenverzahnungen, somit sind Eingriffsstörungen bei Innenverzahnungen häufiger. Alle Hinweise auf Eingriffsstörungen erhalten Sie im Meldungsfenster. Bei einer Innenverzahnung gilt die allgemeine Regel, dass eine Mindestzähnezahldifferenz
\[z_{2} - z_{1} \geq 10\]
eingehalten werden soll. Um jedoch Eingriffsstörungen zwischen Schneidrad und innerverzahntem Rad zu vermeiden, wird meistens noch eine größere Mindestzähnezahldifferenz notwendig. Die folgenden Eingriffsstörungen bei einer Innenverzahnung können im Berechnungsmodul auftreten:
Hinweis: Auch durch Kopfkürzungen am Hohlrad oder am Ritzel, durch eine Vergrößerung des
Eingriffswinkels oder durch eine Vergrößerung des Schrägungswinkels, lassen sich Eingriffsstörungen
vermeiden oder verringern.
Eine Zahnfußeingriffsstörung am Ritzel tritt auf, wenn der Zahnkopf des Hohlrades den Zahnfußausrundungsradius
des Ritzels berührt, also ein Eingriff im nichtevolventischen Bereich. Mit der Verkleinerung des
Profilverschiebungsfaktors \(x_{2}\) und der sich daraus ergebenden Verringerung der Profilverschiebungssumme kann
die Eingriffsstörung behoben werden.
Eine Zahnfußeingriffsstörung am Hohlrad tritt auf, wenn der Zahnkopf des Ritzels den Zahnfußausrundungsradius
des Hohlrades berührt, also ein Eingriff im nichtevolventischen Bereich. Durch eine Verringerung der
Profilverschiebungssumme lässt sich diese Eingriffsstörung beseitigen.
Befinden sich Schneidrad und Innenrad im Eingriff, entsteht bei einer zu kleinen Schneidradzähnezahl eine
Erzeugungs-Eingriffsstörung. Die Erzeugungs-Eingriffsstörung wirkt sich durch einen Verlust an erzeugtem
Evolventenprofil am Zahnkopf des Innenrades aus. Dadurch wird die Eingriffsdauer verkleinert und die
Tragfähigkeit verringert.
Zahnkopfeingriffsstörungen können auftreten, wenn sich die Zahnköpfe von Ritzel und Hohlrad während des Abwälzvorganges außerhalb der Eingriffsebene überschneiden. Bei Zähnezahldifferenzen von
\(\left |z_{2}\right | - z_{1} < 10\)
kommt diese Eingriffsstörung recht häufig vor. Auch bei der Erzeugung von Innenverzahnungen mit
Schneidrädern kann die Zahnkopfeingriffsstörung vorkommen. Die Eingriffsstörung kann durch eine
Änderung der Zähnezahlen oder auch durch eine negative Profilverschiebung verhindert bzw. beseitigt
werden.
Eine Vorschubeingriffsstörung bei der Erzeugung des Hohlrades tritt auf, wenn das gewählte
Schneidrad so groß ist, dass es in Vorschubrichtung die Zähne der Innenverzahnung wegschneidet.
Wird die Profilverschiebungssumme verringert, können Vorschubeingriffsstörungen vermieden
werden.
Wenn beim Innengetriebe das Ritzel so groß ist, dass es beim radialen Einbau die Zähne des Hohlrades berührt, dann tritt eine radiale Einbaustörung auf. Dadurch wird ein radialer Einbau bei einer Innenradpaarung nicht möglich sein. Das bedeutet, dass der Einbau dann nur noch axial erfolgen kann. Diese Eingriffsstörung kommt bei kleinen Zähnezahldifferenzen vor. Eine radiale Einbaustörung kann durch eine Verkleinerung der Profilverschiebungsfaktoren und der Kopfhöhe an Ritzel sowie Hohlrad beseitigt werden.
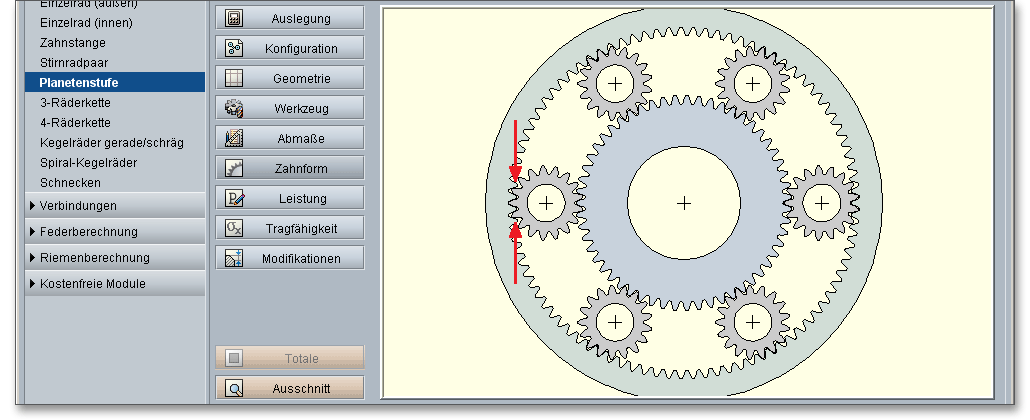
Wenn keine Sonderanforderungen an das Planetengetriebe vorliegen, dann unterscheidet sich die Ausführung
von den außenverzahnten Zahnrädern nicht von der Gestaltung der Zahnrädern für Standgetriebe. Für die
kompakte Bauweise eignen sich eher kleine Räder, die als Vollräder hergestellt werden. Für
größere Übersetzungen werden die Räder meist in einem Stück mit einer Welle ausgeführt.
Scheibenräder werden für größere Räder verwendet. Umlaufende innenverzahnte Räder für
Hochleistungsgetriebe sollten beidseitig gelagert sein, für gering belastete Getriebe eignen sich fliegend
gelagerte Räder.
Der Einbau von Lagern gestaltet sich aufgrund des geringen Raumes im Planetengetriebe schwierig.
Es ist möglich, das Zentralritzel ungelagert in der Verzahnung abzustützen. Das Drehmoment
wird über Zahnkupplungen ein- oder weitergeleitet. Durch den Wegfall der Lager entsteht der
Vorteil, dass sich der Wirkungsgrad erhöht. Auch eine zusätzliche Einrichtung für die Schmierung
der Lager ist nicht mehr notwendig. Das Planetenrad kann auf dem Planetenradbolzen gelagert
werden, der fest mit dem Steg verbunden ist. Der Bolzen kann aber auch im Steg gelagert und fest
mit dem Planetenrad verbunden werden. Für die Lagerung werden meist Gleit- und Wälzlager
genutzt.
Der Steg eines Planetengetriebes kann geteilt oder ungeteilt ausgeführt werden. Der geteilte Steg setzt sich
aus Elementen zusammen, die aus Blechen oder anderem Walzmaterial herausgearbeitet sind. Stege für
höhere Beanspruchungen werden gegossen. Ungeteilte Stege sind sehr drehsteif und unempfindlich
gegenüber Wärmedehnungen. Die Planetenradbolzen können im Steg drehbar gelagert oder fest
eingespannt sein. Wenn die Bolzen mit dem Steg verbunden sind, muss eine entsprechende Sicherung durch
Splinte, Stifte oder Schrauben gegeben sein.
Je nach wirtschaftlichen Gesichtspunkten kann das Gehäuse eines Planetengetriebes gegossen oder
geschweißt werden. Geschweißte Gehäuse werden häufig bei Sondergetrieben und Getrieben verwendet, die
nur eine geringe Masse haben dürfen. Bei Serienfertigung kommen gegossene Gehäuse zum Einsatz. Für
große Getriebe mit einer geringen Masse werden oftmals doppelwandige, geschweißte Stahlgehäuse
verwendet.
Wenn nur wenige Eingabedaten, wie zum Beispiel Eingangsdrehzahl, Leistung und Übersetzungsverhältnis vorliegen, kann die Software entsprechende Vorschläge zu Zähnezahl und Modul auf Knopfdruck liefern.
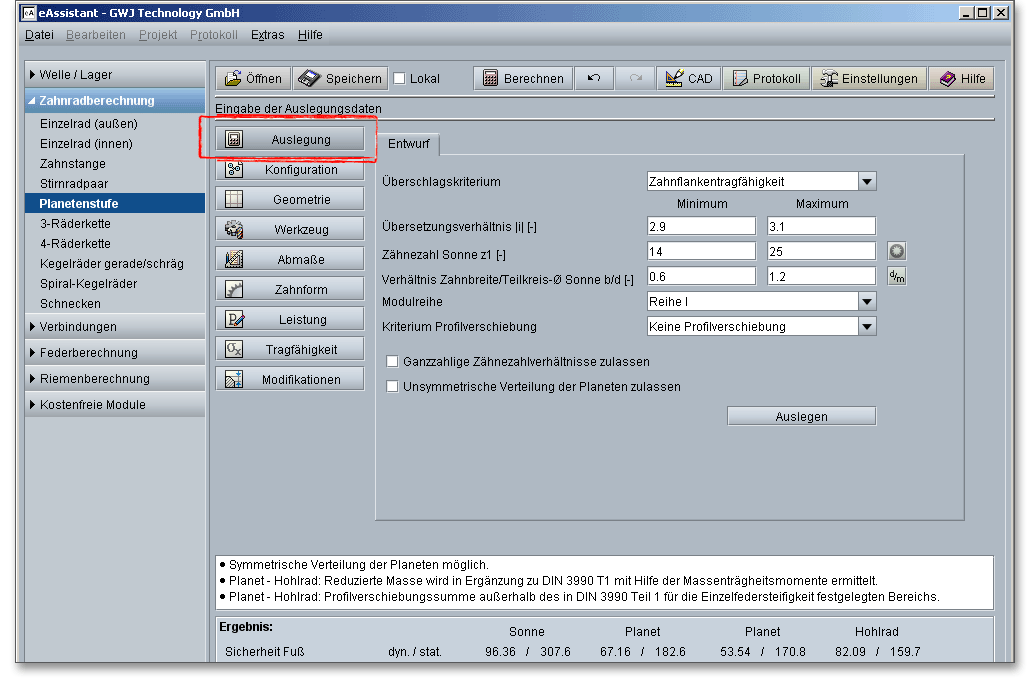
Bevor Sie mit der Auslegung starten, muss die Tragfähigkeit aktiviert werden, sonst ist die Auslegung nicht möglich. Dabei können Sie den Werkstoff für Sonne, Planet und Hohlrad vorgeben oder den Anwendungsfaktor sowie den Schmierstoff anpassen.
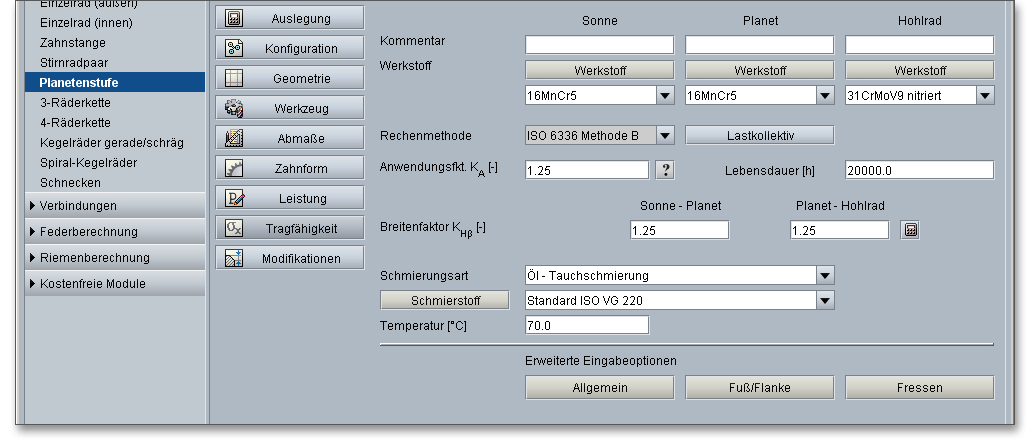
Desweiteren lassen sich vor der Entwurfsauslegung die Leistungsdaten, Abmaße, Werkzeugdaten sowie die
Konfiguration über die entsprechenden Hauptmasken modifizieren. Wenn Sie alle Einstellungen zur
Vorbelegung definiert haben, dann gehen Sie zur Hauptmaske „Auslegung“.
Bevor Sie allerdings mit den weiteren Daten zur Auslegung fortfahren, werfen Sie bitte zunächst einen Blick in das Menü „Einstellungen“. In diesem Menü sind die Mindestsicherheiten für die Fuß- und Flankentragfähigkeit hinterlegt. Diese festgelegten Mindestsicherheiten werden genau so bei der Entwurfsauslegung mit berücksichtigt.
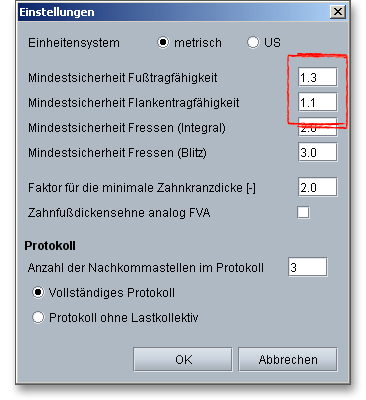
Hinweis: Für Standardindustrieanwendungen können die Standardwerte für die Mindestsicherheit von 1,3
für die Zahnfußtragfähigkeit und 1,1 für die Flankentragfähigkeit so übernommen werden. Bei
Anwendungen mit einer großen Schadensfolge oder wo Personenschäden auftreten können, sollten größere
Mindestsicherheiten gewählt werden. Bei einem kleineren Modulbereich (< 1), beispielsweise in der
Feinwerktechnik, bieten sich kleinere Mindestsicherheiten an.
In der Hauptmaske zur Entwurfsauslegung werden jetzt die restlichen Eingaben vervollständigt. Dabei lässt sich für das Übersetzungsverhältnis, Zähnezahl für die Sonne und Verhältnis Zahnbreite/Teilkreisdurchmesser immer ein bestimmter Bereich vorgeben. Alternativ zum Vorgabebereich für die Zähnezahl der Sonne kann mit einem Klick auf den Button auch ein Bereich für die Zähnezahl des Hohlrades vorgeben werden. Über den entsprechenden Button lässt sich auch zwischen Verhältnis Zahnbreite/Teilkreisdurchmesser und Verhältnis Zahnbreite/Modul umschalten.

Wenn Sie alle Eingaben vorgenommen haben, klicken Sie auf den Button „Auslegen“. Jetzt berechnet die Software alle möglichen Varianten durch und eine Liste für mögliche Lösungen wird anschließend angezeigt.
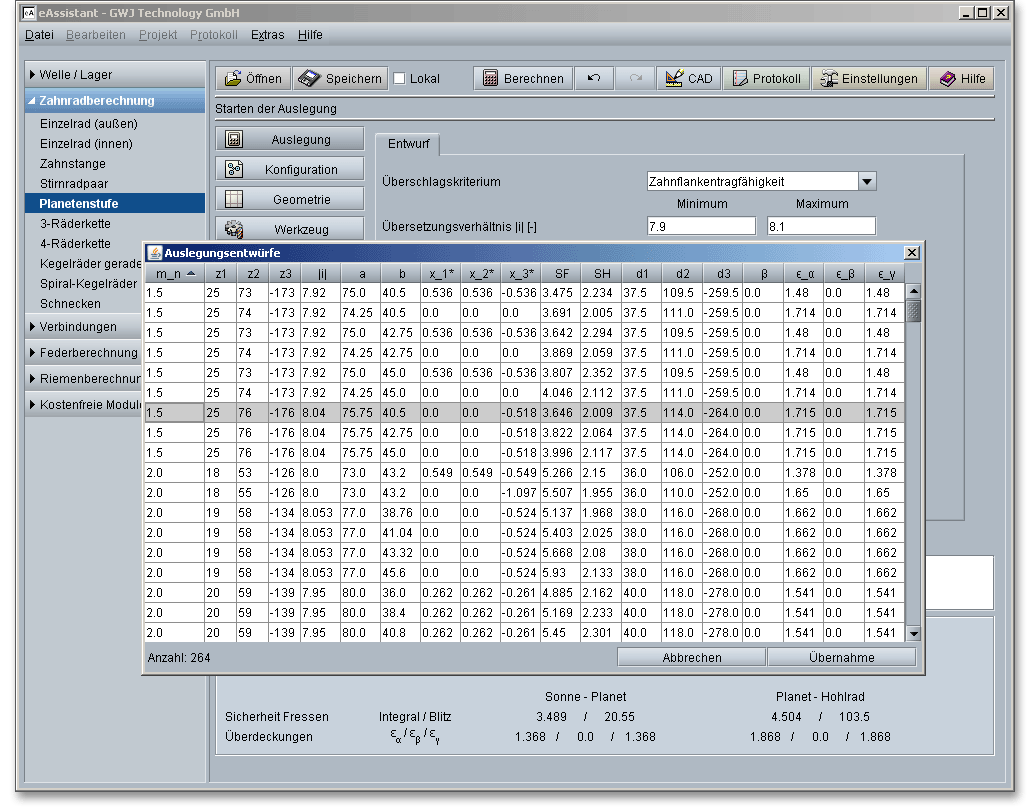
Bei der Anzeige der gefundenen Vorschläge können Sie die Liste umsortieren, indem Sie auf die jeweilige
Spaltenüberschrift klicken. Soll die Spalte in umgekehrter Reihenfolge sortiert werden, klicken Sie erneut auf
die Spaltenüberschrift. Wählen Sie aus der Liste einen Vorschlag und klicken Sie auf „Übernehmen“. Die
ausgewählten Werte werden jetzt in die Software eingetragen und man erhält so einen ersten
Berechnungsvorschlag, der sich anschließend verfeinern und weiterverarbeiten lässt. Somit kommen Sie auf
einem schnellen Weg zu einer brauchbaren Lösung, mit der Sie starten können, um Sie später nach Ihren
eigenen Kriterien auslegen zu lassen.
Das Berechnungsmodul enthält ein Meldungsfenster, in denen Informationen, Hinweise oder Warnungen aufgelistet werden. Die eAssistant-Software erkennt bereits während der Dateneingabe auftretende Fehler und zeigt Ihnen sogleich Lösungsvorschläge im Meldungsfenster an. Wenn Sie die verschiedenen Hinweise und Warnungen beachten und befolgen, lassen sich schnell Fehler in Ihrer Berechnung beheben.

Bewegen Sie den Mauszeiger über ein Eingabefeld oder über einen Button, so erhalten Sie zusätzliche Informationen, die Ihnen in der Kurzhilfe angezeigt werden.
Die Ergebnisse werden bereits während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld angezeigt. Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Dadurch werden jegliche Veränderungen der Eingabewerte auf die Ergebnisse schnell sichtbar. Werden die Mindestsicherheiten nicht erfüllt, so wird das Ergebnis mit einer roten Markierung angezeigt. Grundsätzlich können Sie jede Eingabe mit der Enter-Taste oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können Sie mit der Tab-Taste durch die Eingabemaske springen oder nach jeder Eingabe auf den Button „Berechnen“ klicken. Auch hierbei werden die Werte entsprechend übernommen und die Ergebnisse sofort in der Übersicht angezeigt.

Nach Abschluss Ihrer Berechnungen haben Sie die Möglichkeit, ein Protokoll zu generieren. Klicken Sie dazu auf den Button „Protokoll“, um das Protokoll zu öffnen.

Das Protokoll enthält ein Inhaltsverzeichnis. Hierüber lassen sich die gewünschten Ergebnisse schnell aufrufen. Es werden Ihnen alle Eingaben sowie Ergebnisse aufgeführt. Das Protokoll steht Ihnen im HTML- und im PDF-Format zur Verfügung. Sie können das erzeugte Protokoll zum Beispiel im HTML-Format abspeichern, um es später in einem Web-Browser wieder oder im Word für Windows zu öffnen.
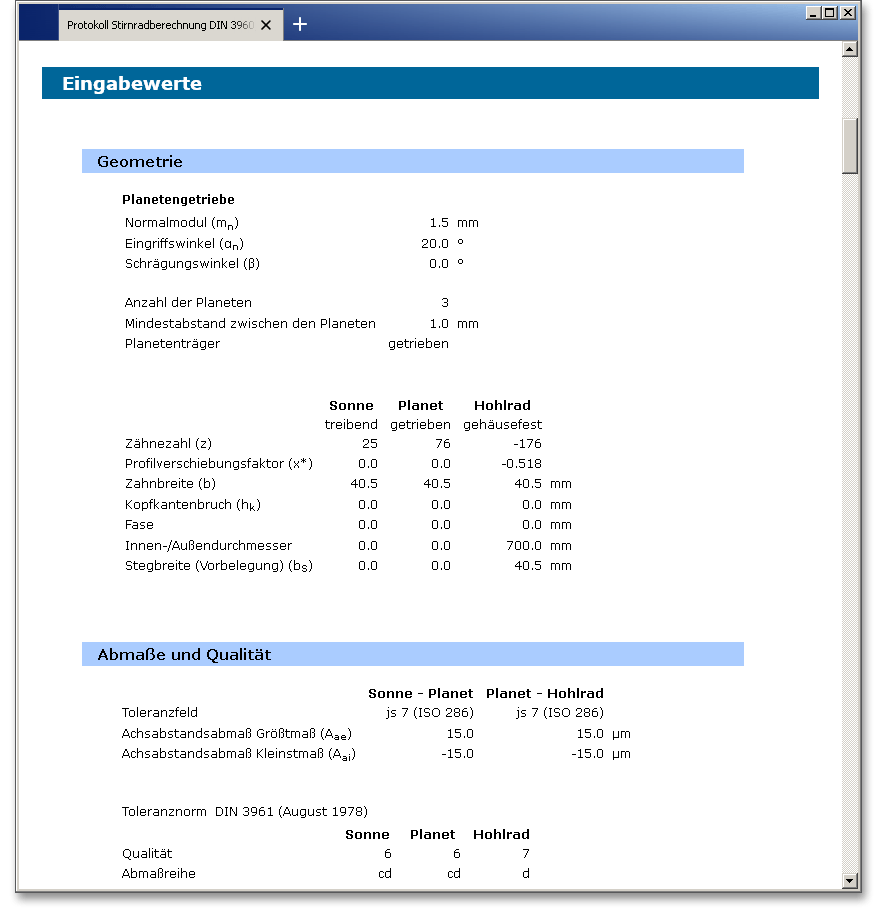
Das Berechnungsprotokoll lässt sich drucken oder speichern:
Nach der Durchführung Ihrer Berechnung können Sie diese speichern. Sie haben dabei die Möglichkeit, entweder auf dem eAssistant-Server oder auf Ihrem Rechner zu speichern. Klicken Sie auf den Button „Speichern“ in der obersten Zeile des Berechnungsmoduls.

Um die Berechnung lokal auf Ihrem Rechner zu speichern, müssen Sie die Option „Lokal“ im Berechnungsmodul aktivieren.
Haben Sie diese Option nicht aktiviert, so öffnet sich ein neues Fenster und Sie können Ihre Berechnung auf dem eAssistant-Server speichern. Geben Sie unter „Dateiname“ den Namen Ihrer Berechnung ein und klicken Sie auf den Button „Speichern“.
Mit dem Button „Zurück“ können Sie vorhergegangene Eingaben zurücksetzen. Wenn Sie eine rückgängiggemachte Eingabe wiederherstellen wollen, dann klicken Sie auf den Button „Vorwärts“.

In der obersten Zeile des Berechnungsmoduls finden Sie den Button „CAD“.

Auf der Basis Ihrer Berechnung lassen sich über diesen Button „CAD“ die Verzahnungen in einem
2D-DXF-Format oder über das eAssistant CAD-PlugIn in einem 3D-CAD-System, wie zum Beispiel
SOLIDWORKS oder Solid Edge, erzeugen.
Klicken Sie im Berechnungsmodul auf den Button „CAD“, anschließend auf den Menüpunkt „DXF-Ausgabe“. Damit kann die exakte Zahnform von beliebigen evolventischen Verzahnungen im 2D-DXF-Format mit den unterschiedlichen Einstelloptionen generiert werden.

Für die DXF-Ausgabe sind die folgenden Einstelloptionen möglich:
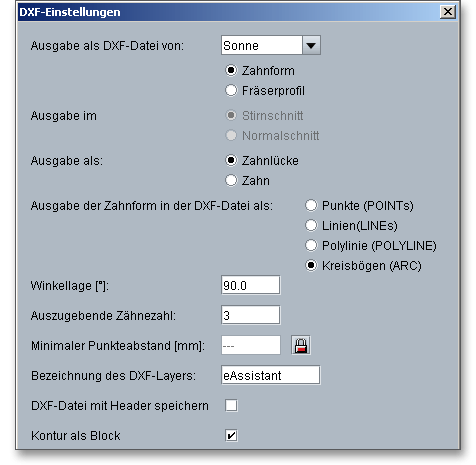
Wenn Sie Ihre Einstellungen angepasst haben, dann klicken Sie auf den Button „OK“. Ein Windows-Dialog zum Speichern der Datei öffnet sich.
Sie können die DXF-Datei jetzt auf Ihrem Rechner speichern. Geben Sie einen Dateinamen ein und klicken Sie
auf den Button „Speichern“. Die Dateiendung „dxf“ müssen Sie hier nicht angeben, da diese automatisch an
den Dateinamen angehängt wird.
Diese Funktion ermöglicht das Generieren der Geometrie von Stirnradpaaren als 3D-CAD-Modell im STEP-und IGES-Format. Sowohl das STEP- als auch das IGES-Format sind standardisierte Austauschformate für 3D-Modelle und können in fast jedes CAD-System importiert werden.
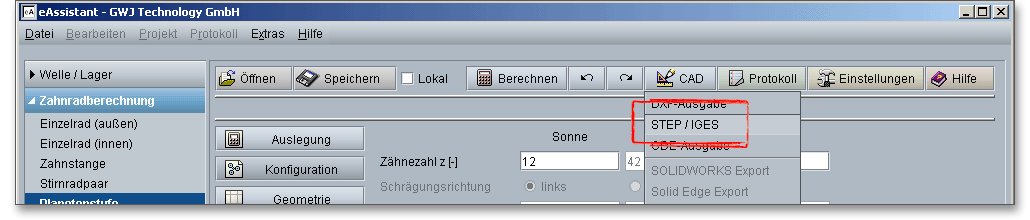
Im Einstellungsmenü für die STEP- und IGES-Ausgabe stehen Ihnen verschiedene Funktionen zur Auswahl, um den Export individuell anzupassen. Dabei lässt sich die Geometrie als Volumenmodell mit einem oder allen Zähnen oder auch als Flächenmodell der Zahnlückengeometrie erzeugen. Beim Export können Sie außerdem den Grad der Genauigkeit auf einen gewünschten Wert festlegen.
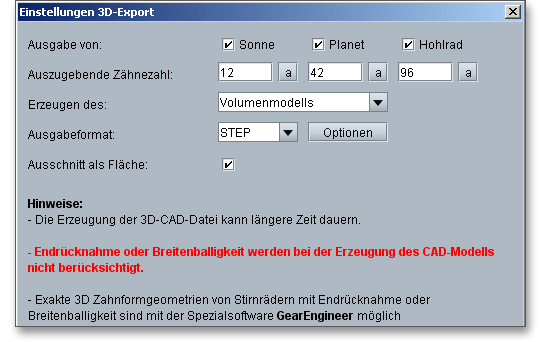
Eine weitere Erweiterung ist das GDE-Ausgabeformat. GDE steht hier für Gear Data Exchange. Dieses Format ist in der VDI/VDE Richtlinie 2610 definiert und wird bereits von vielen Messmaschinenherstellern unterstützt. Damit können die Verzahnungsdaten von Stirnrädern und Zahnwellen direkt aus der Berechnung in die Software der Messmaschine eingelesen werden. Mit nur wenigen Mausklicks lässt sich dann ein Messprogramm erstellen. Dabei werden Übertragungsfehler vermieden und es kann mit einer einheitlichen Messanweisung gearbeitet werden.
Auf Basis Ihrer Berechnung können mit dem eAssistant CAD-PlugIn schräg- und geradverzahnte Stirnräder (außen- und innenverzahnt) featurebasiert im 3D automatisch erstellt werden. Toleranzen, Kopfkantenbruch und Profilverschiebung werden mit berücksichtigt und es wird die exakte Zahnform modelliert. Klicken Sie auf den Button „CAD“, anschließend wählen Sie das entsprechende CAD-System für den Export aus.

Öffnen Sie jetzt das 3D-CAD-System. Über einen integrierten Menüpunkt „eAssistant“ im CAD-System
können Sie sofort mit der Generierung der berechneten Stirnräder starten.
Hinweis: Das entsprechende eAssistant CAD-PlugIn muss bereits auf Ihrem CAD-Rechner installiert
sein.
Zu den entsprechenden 2D-Ableitungen der Zahnräder können jederzeit per Mausklick auch die Herstelldaten
auf eine Zeichnung plaziert werden.
Hinweis: Benötigen Sie nähere Informationen zum eAssistant CAD-Plugin, so können Sie sich
jederzeit gern an uns wenden. Weitere Einzelheiten erfahren Sie auch über unsere Webseite
www.eAssistant.eu oder in dem Hilfe-Manual zum eAssistant CAD-PlugIn, welches Sie auch auf der
Webseite finden können.
Über den Button „CAD \(\Rightarrow \) Herstelldaten“ lassen sich die Herstelldaten alternativ auch als Textdatei speichern.
Die Zahnform einer Zahnlücke kann als Koordinatentextdatei sowohl im Stirn- als auch im Normalschnitt ausgegeben werden.
Klicken Sie auf den Button „Einstellungen“ in der obersten Zeile des Berechnungsmoduls. Diese Option gibt Ihnen die Möglichkeit, Standardeinstellungen im Berechnungsmodul zu ändern.