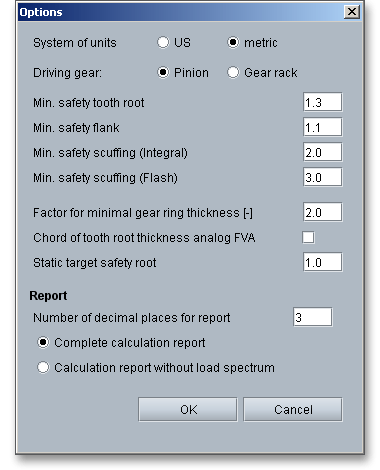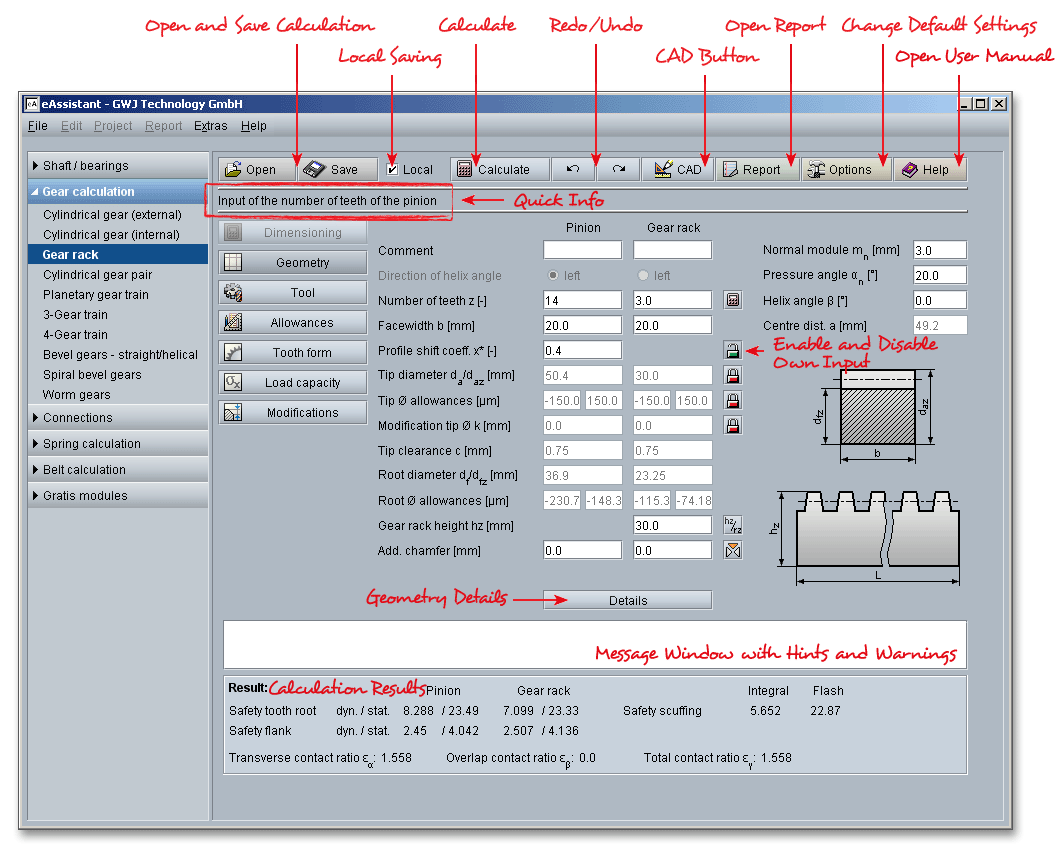
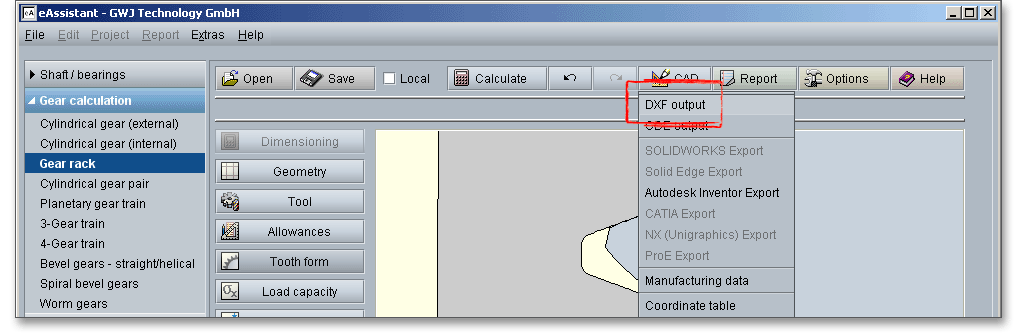
Please login with your username and your password. To start the calculation module for gear racks, please click the menu item ‘Gear calculation’ on the left side and then select ‘Gear rack’.

This gear calculation module allows a simple calculation of the geometry and load capacity of rack-pinion gear pairs. The geometry calculation is based on DIN 3960, DIN 3961, DIN 3964, DIN 3967, DIN 3977 and DIN 868, the calculation of the load capacity is based on DIN 3990 Method B, ISO 6336 Method B and ANSI/AGMA 2101-D04. Spur and helical involute pinions are possible to calculate. Profile shift, addendum chamfer and allowances will be taken into consideration. The number of teeth or alternatively, the length of the gear rack can be specified. Rectangular or round cross section gear rack designs are possible.

In theory a gear rack is a section of a spur gear with an infinitely large pitch diameter, resulting in an involute
profile that is essentially a straight line. Gear-rack pairings are important components in that they are a means of
converting rotational motion into linear motion and vice versa. The rack can be used to determine the basic
gear parameters. Gear racks mate with an external spur gear (pinion) and can be both spur and
helical.
All important calculation results will be calculated during every input and will be displayed in the result panel. A
recalculation occurs after every data input. Any changes that are made to the user interface take effect
immediately. Press the Enter key or move to the next input field to complete the input. Alternatively, use the Tab
key to jump from field to field or click the ‘Calculate’ button after every input. Your entries will be also confirmed
and the calculation results will displayed automatically. If the result exceeds certain values, the result will be
marked red.
The normal module \(m_{n}\) is one of the basic parameters in the gear geometry and describes the size of a gear. The module is defined as the ratio of the pitch diameter to the number of teeth of a gear. Note that the larger the module the larger the teeth. The value of the module is defined in millimeters. In order to limit the number of the gears, the module has been standardised in preferred series 1 and 2 (see following tables). The calculation with the eAssistant software is possible with any modules including several decimal places.
| Series of Modules in mm According to DIN 780 Series 1 (Part 1)
| |||||||
| 0.05 | 0.06 | 0.08 | 0.10 | 0.12 | 0.16 | 0.20 | 0.25 |
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| Series of Modules in mm According to DIN 780 Series 1 (Part 2)
| ||||||||
| 1.25 | 1.5 | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
| 10 | 12 | 16 | 20 | 25 | 32 | 40 | 50 | 60 |
| Series of Modules in mm According to DIN 780 Series 2 (Part 1)
| ||||||||
| 0,055 | 0.07 | 0.09 | 0.11 | 0.14 | 0.18 | 0.22 | 0.28 | 0.35 |
| 0.45 | 0.55 | 0.65 | 0.75 | 0.85 | 0.95 | 1,125 | 1,375 | 1.75 |
| Series of Modules in mm According to DIN 780 Series 2 (Part 2)
| |||||||
| 2.25 | 2.75 | 3.5 | 4.5 | 5.5 | 7 | 9 | 11 |
| 14 | 18 | 22 | 28 | 36 | 45 | 55 | 70 |
The pressure angle is the angle between the line-of-action and the common tangent to the pitch
circles. With an increasing distance from the base circle, the profile angles \(\alpha _{y}\) increase too. The most
common pressure angle now in use for spur gears is \(20^{\circ }\). This pressure angle is usually preferred
due to its stronger tooth shape and reduced undercutting. The \(25^{\circ }\) pressure angle has the highest
load-carrying ability, but is more sensitive to center-distance variation and hence runs less quietly. The
choice is dependent on the application. The default startup setting for the pressure angle is set to
\(20^{\circ }\).
For spur gears the helix angle is \(\beta \) = \(0^{\circ }\), for helical gears the angle \(\beta \) is up to \(45^{\circ }\) due to the fact that the teeth for a helical gear are inclined by the angle. \(45^{\circ }\) is also the maximum value that you can enter into the input field for the helix angle. For an external gearing a right-hand teeth and a left-hand teeth can only mesh correctly. For internal gearings pinion and gear must have the same direction.
Please note: Calculation with helix angle greater than 45 degree is possible. If you want to use this option,
please contact us.
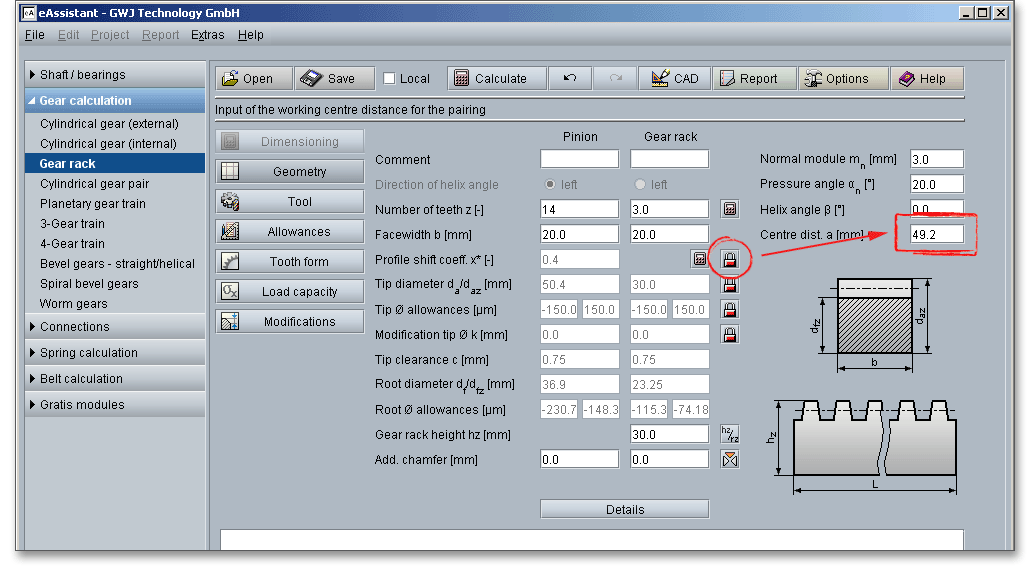
The centre distance \(a\) is the distance between the axes. In case of changing the normal module \(m_{n}\), the centre distance is determined automatically.
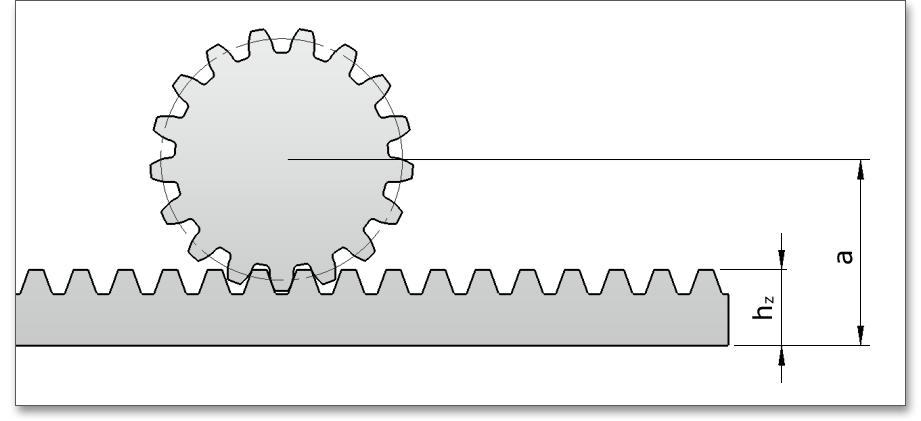
The centre distance can be determined from the profile shift of the pinion and vice versa. It is also possible to specify the centre distance manually. This determines the profile shift coefficient of the pinion. Click the ‘Lock’ button next to the input field of the profile shift coefficient. The input field for the profile shift coefficient will be disabled and you can enter a value for the centre distance.
After adding an helix angle, you can specify the helix direction of pinion and gear rack. Please keep in mind that both gears of a meshed pair must have the same helix angle \(\beta \). However, the helix directions must be opposite, i.e., a left-hand mates with a right-hand helix.

Select the option ‘left’ for the pinion. That means: Pinion is left-handed, pinion is right-handed.

Select the option ‘left’ for the gear rack. That means: Pinion is right-handed, gear rack is left-handed.

The number of teeth of a gear describes the number of the teeth on the full rim. The number of teeth is positive
for external gears and negative for internal gears. Please note that the smaller the number of teeth the larger the
influence of the profile shift.
Please note: A calculation with non-integer number of teeth, i.e., number of teeth with decimal places. If you
want to use this option, please contact us.
Click the ‘Calculator’ button to open the window and to dimension the length or, alternatively, the number of teeth of the gear rack.
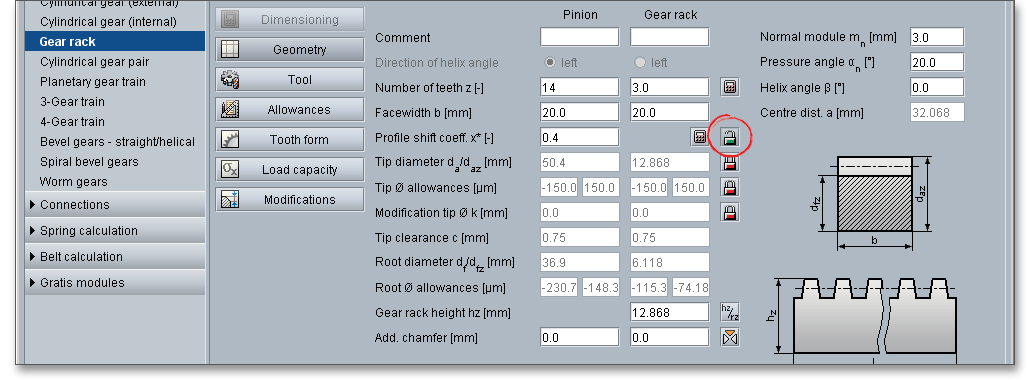
Enter the number of teeth and confirm your input by clicking the Enter key. The optimal length of the gear rack is shown. Alternatively, you can specify the length of the gear rack in order to get a recommendation for the number of teeth of the gear rack. To do so, click the ‘Lock button’ to enable the input field and enter a value. Confirm the value with Enter. The number of teeth of the gear rack is automatically determined.

The facewidth \(b\) is the length of the gear teeth as measured along a line parallel to the gear axis.
The following table shows some additional information about the facewidth \(b\) as well as minimum number of teeth \(z\).
| Standard Values for the Facewidth \(b\) and Minimum Number of Teeth \(z\)1
| ||
| Teeth, machine-cut | Gears on rigid shafts, that run in roller or excellent plain bearings, rigid substructure | \(b \leq 30\ldots 40\cdot {m}\) |
| Gears in usual gear boxes, roller or plain bearings | \(b \leq 25\cdot {m}\) | |
| Gears on steel constructions, beams and suchlike | \(b \leq 15\cdot {m}\) | |
| Gears with excellent bearing in high duty gearings | \(b \leq 2\cdot {d_{1}}\) | |
| Teeth, cast roughly | Overhung gears | \(b \leq 10\cdot {m}\) |
| Gears with high circumferential velocity\((\upsilon > 4\ m/s)\) and considerable power,
when \(\varepsilon _{\alpha } > 1.5\) | \(z_{1} \geq 16\) | |
| Gears with mean circumferential velocity\((\upsilon = 0.8\ldots 4\ m/s)\) | \(z_{1} \geq 12\) | |
| Gears with low circumferential velocity\((\upsilon < 0.8\ m/s)\) or for low power for subordinated
purposes | \(z_{1} \geq 10\) | |
| Basically external gearings | \(z_{1} + z_{2} \geq 24\) | |
| Basically internal gearings | \(z_{2} \geq z_{1} + 10\) | |
| 1 from: Karl-Heinz Decker: Maschinenelemente: Gestaltung und Berechnung, 1992, p. 506, table
23.2
| ||
The tooth form of a gear rack cannot be changed by the profile shift. The profile shift is only applied to the pinion. Profile-shifted gears can be meshed with the gear rack. A shift in the utilized profile range compared to the normal position is called the profile shift. The profile shift affects the tooth form because the tool is shifted by the value \(xm\) towards or away from the tip circle. A profile shift is used to avoid meshing interferences. The calculation of the tip diameter \(d_{a}\) and root diameter \(d_{f}\) includes the profile shift coefficient \(x\). According to DIN 3960 the profile shift is
The profile shift of the pinion can be freely chosen. Please note that no meshing interferences occur. Please note that no meshing interferences occur. In case meshing interferences occur, you will get an appropriate message in the message window.
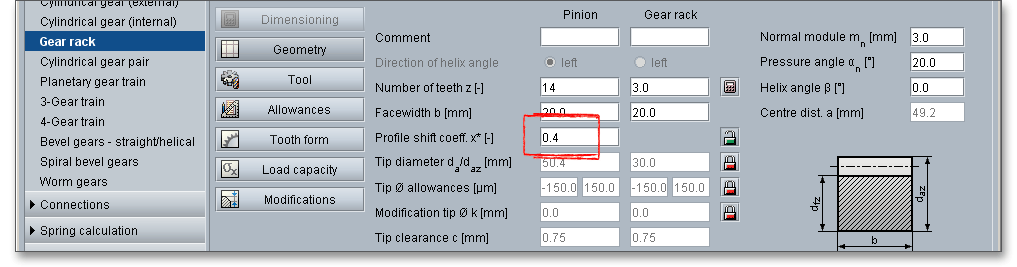
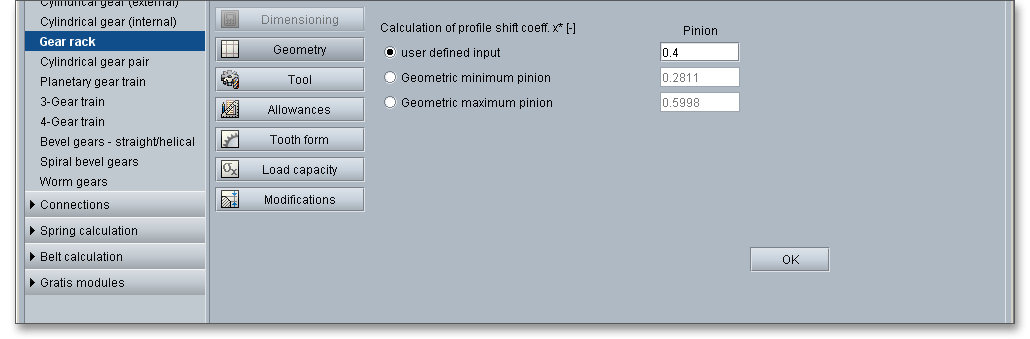
Here you have the option of dimensioning or optimizing the profile shift coefficient. To optimize the profile shift coefficient, click on the ‘Calculator’ button. In addition to the option ‘user-defined input’, the following two options are available for selection: ‘Geometric minimum’ and ‘Geometric maximum’. Here the possible limits of the profile shift, i.e. the minimum and maximum profile shift that can be executed with respect to the undercut limit and topland limit.
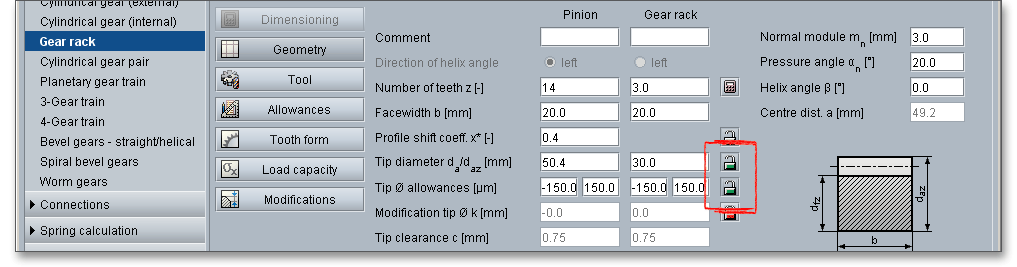
The tip diameter \(d_{a}\) depends on the module and will be determined by the program automatically. If you change
the profile shift, the tip diameter will change, too. There is the possibility to enable the tip circle using the ‘Lock’
button. Now you can add and modify the tip diameter very easily. Please note that the tip diameter has an
influence on the modification of the tip diameter. Click on the button again to disable the input field. The
value is determined again according to DIN. In case you use a special tool, the tip diameter can be
changed by a tool customization. Find out more about the tool data in the section ‘The input of tool
data’.
The tip diameter allowance is determined according to DIN. Click on the ‘Lock’ button to enable the input field and enter your own value. If your values are out of range of the DIN, you will get an information in the message window. Click on the ‘Lock’ button and the input field is disabled again. The allowances are determined according to DIN.
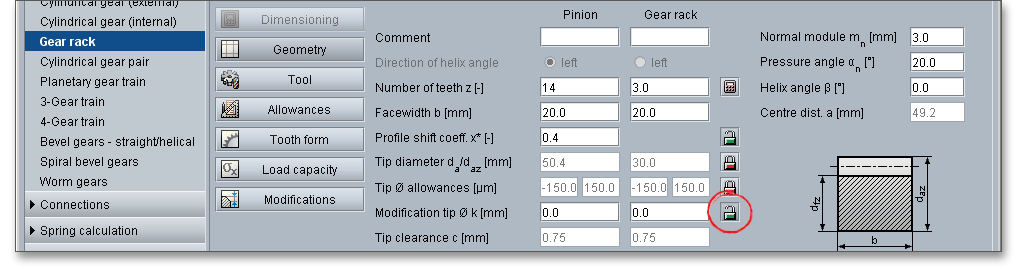
The modification of the tip diameter \(k\) is automatically determined by the program that a sufficient tip clearance is available. For external gears the modification of the tip diameter is \(k \le 0\). Click on the ‘Lock’ button to enable the input field and enter your own value. Such a modification of the tip diameter has an effect on the tip diameter.
Clearance \(c\) is the distance between the root circle of a gear and the addendum circle of its mate. A certain clearance between the gears is necessary for a smooth operation without jamming.
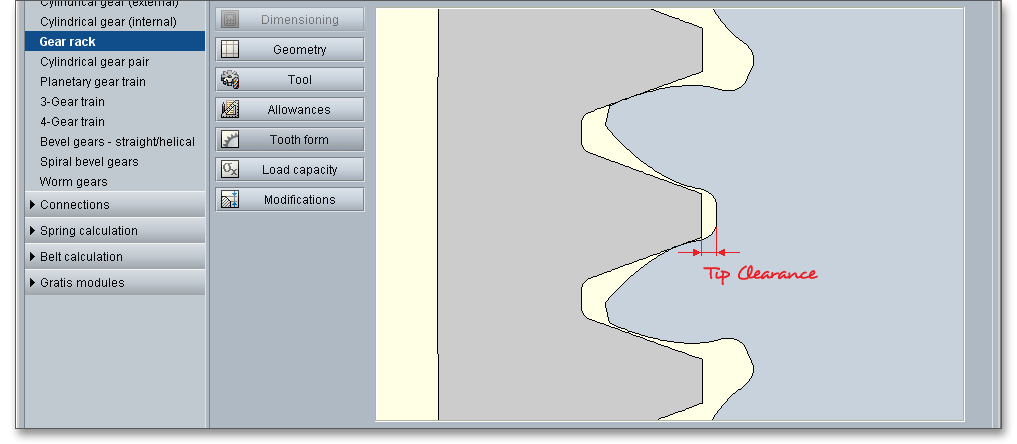
A distinction is made between two different kind of clearances. There is the tip clearance \(c\) and the backlash \(j\). Standard gears have got a basic rack profile with a addendum coefficient \(h_{a} = m\) or a tool basic rack profile with \(h_{fp} = m\). The dedendum coefficient \(h_{f}\) of the basic rack profile or the addendum coefficient \(h_{ap}\) of the tool basic rack profile has to be larger due to ensure that tip and root circle of the gears are not in contact.
If the gears are of standard tooth proportion design and operate on standard center distance, they would
function ideally with neither backlash nor jamming. The general purpose of backlash is to prevent gears from
jamming and making contact on both sides of their teeth simultaneously. Any error in machining which tends to
increase the possibility of jamming makes it necessary to increase the amount of backlash. Consequently, the
smaller the amount of backlash, the more accurate must be the machining of the gears. Runout of both gears,
errors in profile, pitch, tooth thickness, helix angle and centre distance - all are factors to consider in the
specification of the amount of backlash. In order to obtain the amount of backlash desired, it is necessary to
change the tooth thickness or tooth space allowances (please see also section 7.4.8 ‘Backlash Normal
Plane’).
The root diameter \(d_{f}\) depends upon the module, the profile shift and addendum coefficient of the basic rack profile.
The root diameter is determined by the program. Therefore, the root diameter occurs as a result of the
calculation.
The allowances of root result from your calculation and will be determined automatically. The allowances depend upon the tooth thickness allowances. For instance, if you enter the value ‘0’ for a gear, then the allowances of root become ‘0’ for this gear as well.

Enter the height of the gear rack here. Rectangular or round cross section gear rack designs are possible.

Use the button ‘\(h_{z}\)/\(r_{z}\)’ to switch between the gear rack height \(h_{z}\) and the gear rack radius \(r_{z}\). An illustration appears right next to the button.

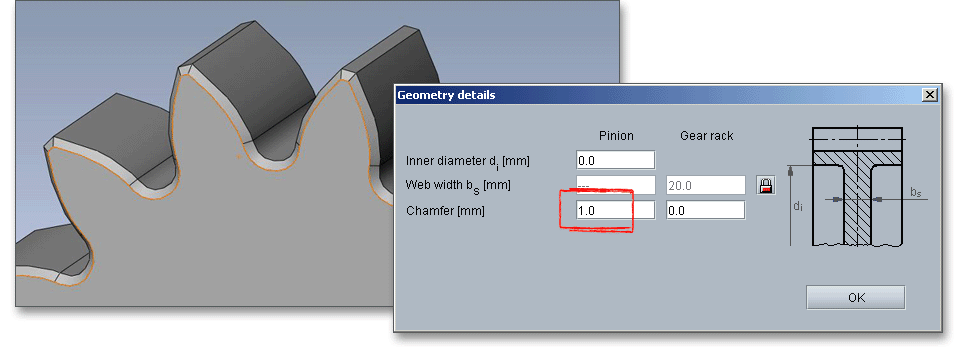
The tooth ends of a gear are often rounded or chamfered. A chamfer is a small angled surface added on the end of a shaft along an edge. For the calculation you can consider the addendum chamfer. Meshing interferences can be removed by the addendum chamfer. As an alternative for the addendum chamfer, it is possible to define a tip corner radius instead of the addendum chamfer. Click the button to choose between addendum chamfer and tip corner radius. The tip corner radius can be specified either as a radial size or as a radius.

Please Note: If you define the geometry of the gear pair, you are able to look at the tooth form. Click on the button ‘Tooth form’ and select ‘Total view’ or ‘Detail view’ (find more information on the tooth form and its functions in section 7.5 ‘Representation of Gear Tooth Form’). Click the button ‘Geometry’ and you get to the geometry input again.
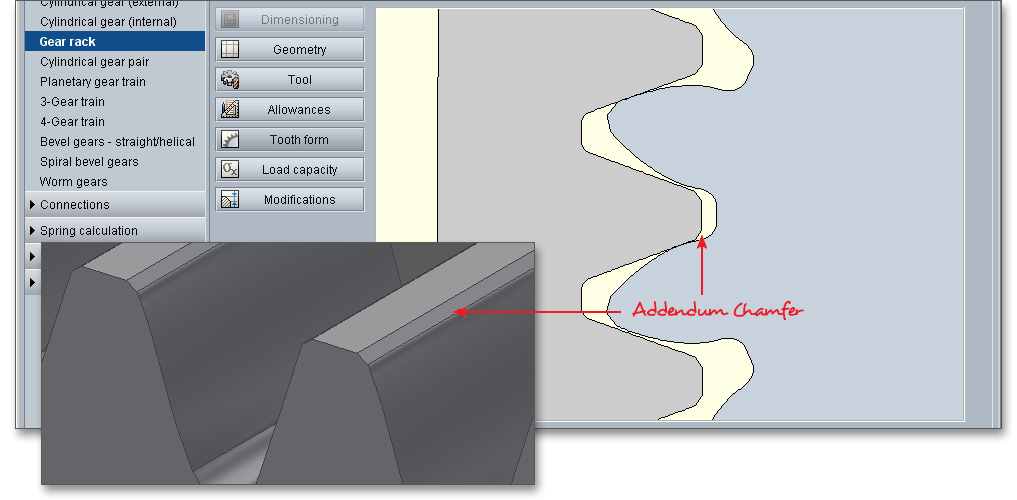
As an alternative to the addendum chamfer, a tip corner radius can be specified. This can be defined
either as a radial amount or directly as a radius. The selection is marked by the colored arrow. The
radius is entered directly for the tip radius, the radial amount is entered for the tip radius (Rad.). If
you enter the tip radius directly as a value, you will receive the corresponding radial amount in the
calculation report. In the case of tip corner radius or addendum chamfer, the tip form diameter is
smaller than the tip circle diameter by twice the radial amount \(h_{K}\). Please see section ?? to find an
illustration.
Click the button ‘Details’ to open additional input options, for example the input of the inner diameter.
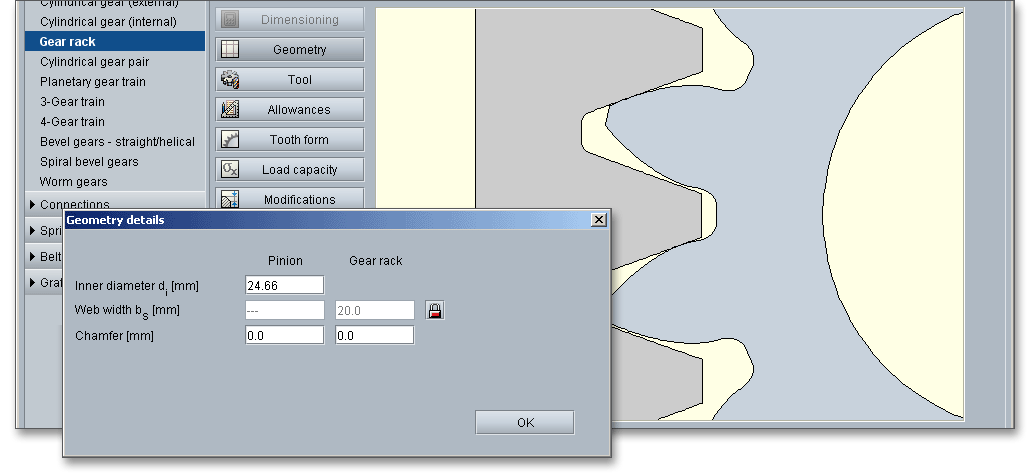
The inner diameter can only be defined for the pinion. It should be kept in mind that the inner diameter has to be
smaller than the root diameter \(d_{f}\). In case the inner diameter is larger than \(d_{f}\), then the program automatically
corrects the value and enters the maximum value for the inner diameter. An appropriate message appears in the
message window.
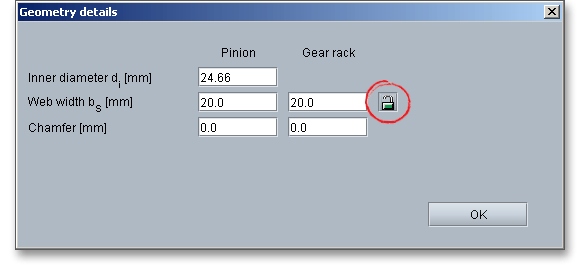
The web width can be considered here. The web width is shown in the figure next to the input field. There is the
possibility to modify the web width by using the ‘Lock’ button.
The ‘Lock’ button is still disabled. Enter the values for the inner or outer diameter into the input field. Then the ‘Lock’ button is enabled and the web width gets the same value as the facewidth. In case the web width is smaller than the facewidth, then the gear body stiffness is affected due to the gear body coefficient \(C_{R}\). The tooth spring stiffness changes which affects again the load capacity.
The chamfer can be considered. This reduces the calculated facewidth for the calculation of the load capacity of the tooth root and tooth flank.
For the selection of the manufacturing process you have to consider the material, size of the gear, quantity, gear type (external or internal gears) and accuracy. The many methods of making gear teeth must be considered as well. eAssistant distinguishes between gear-tooth cutting and gear hobbing.
Please note: If you want to add some own notes, comments or a description, then use the comment
line.
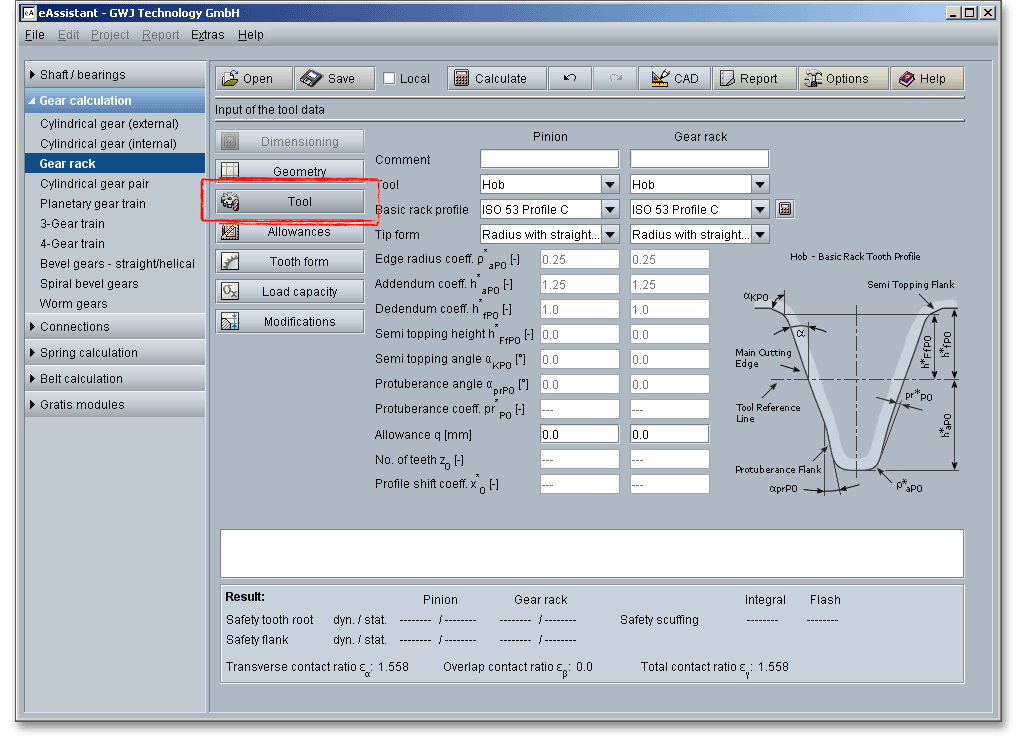
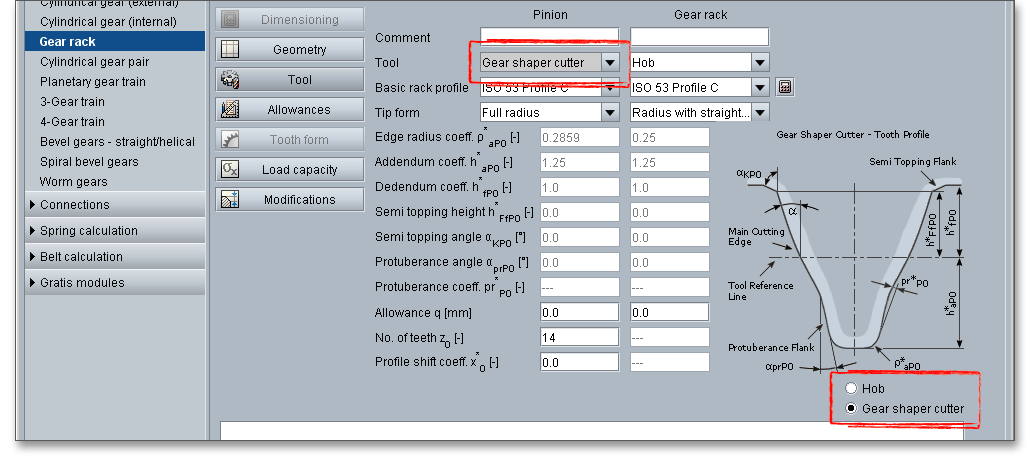
The most important manufacturing processes are gear hobbing and gear shaping. Select either the tool ‘Hob’ or ‘Gear shaper cutter’ by clicking the listbox. A ‘Constructed involute’ is also available. Basically, the selection of the tool depends on the gear type (external or internal gears). The external gears can be produced by cutting wherein the gear cutting tool is a hob.

The hobbing is the most widely used method of cutting gear teeth. The hobbing process is quite advantageous in cutting gears with very wide facewidth. A very high degree of tooth-spacing accuracy can be obtained with hobbing. With regard to accuracy, hobbing is superior to the other cutting processes. A wide variety of sizes and kinds of hobbing machines are used. The rotating hob has a series of rack teeth arranged in a spiral around the outside of a cylinder, so it cuts several gear teeth at one time. To generate the full width of the gear, the hob slowly traverses the face of the gear as it rotates. Thus, the hob has a basic rotary motion and an unidirectional traverse at right angles. Both movements are relatively simple to effect, resulting in a very accurate process.
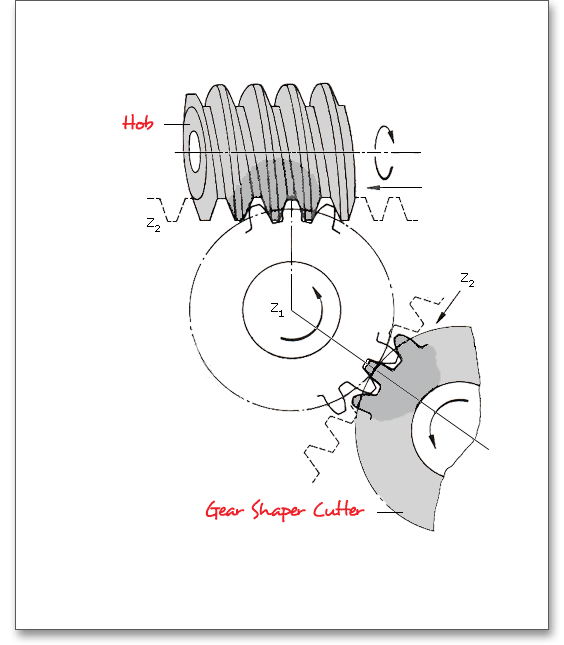
The shaping process is a gear-cutting method in which the cutting tool is shaped like a pinion. If a gear is provided with cutting clearance and is hardened, it may be used as a generating tool in a gear shaper. The cutter reciprocates while it and the gear blank are rotated together at the angular-velocity ratio corresponding to the number of teeth on the cutter and the gear. The teeth on the gear cutter are appropriately relieved to form cutting edges on one face. Although the shaping process is not suitable for the direct cutting of ultra-precision gears and generally is not as highly rated as hobbing, it can produce precision quality gears. Usually it is a more rapid process than hobbing. Two outstanding features of shaping involve shouldered and internal gears. For internal gears, the shaping process is the only basic method of tooth generation.
In addition to the hob and the gear shaper cutter, you can also select the entry ‘Constructed involute’ as a tool. In case internal gears cannot be shaped with a gear shaper cutter, the tooth form calculation is still possible by using the constructed involute. This specifically applies for applications in the precision mechanics. This method allows a generation of the tooth form with a constant root fillet radius.

The representation shows either the hob basic rack profile or the gear shaper cutter tooth profile. The radio buttons enable you to choose one of the graphical representation.
To mesh two gears with each other, the parameters have to be coordinated. The standard basic rack tooth profile is standardized in DIN 867. A gear with an infinite number of teeth will have straight lines for both the pitch and the base circles. The involute profile will be a straight line. The rack can be used to determine the basic parameters. Racks can be both spur and helical. A rack will mesh with all gears of the same pitch. The pressure angle and the gears pitch radius remain constant regardless of changes in the relative position of the gear and rack. The tool standard basic rack profile is the counter profile of the standard basic rack tooth profile.
The following standard basic rack profiles are available for your calculation. Choose your profile from the listbox.
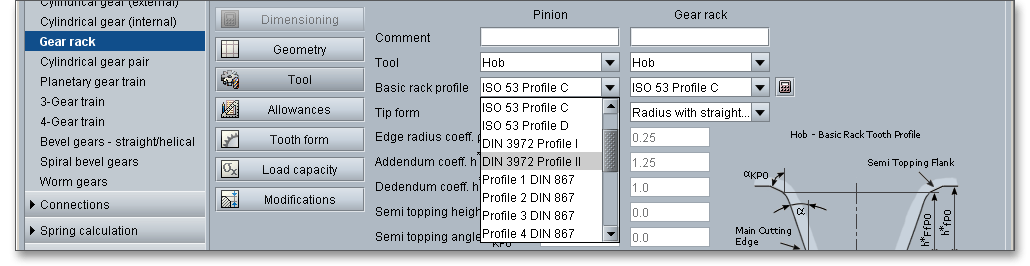
In addition to the standard basic rack profiles, you can also select a protuberance tool. When part of the involute profile of a gear tooth is cut away near its base, the tooth is said to be undercut. By using a protuberance tool an undercut near the root can be generated. Grinding notches at the tooth flank can be avoided during the grinding. That provides relief for subsequent finishing operations (see section 7.3.5 ‘Protuberance’).
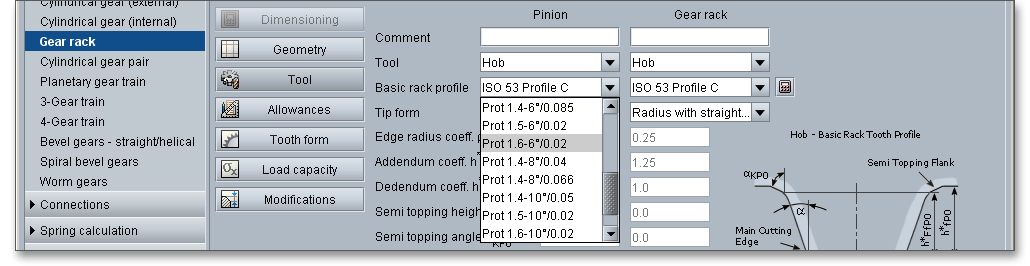
You can select the following profiles:
Please Note: If you select ‘user defined input’, then the input fields for the edge radius, the addendum coefficient and the dedendum coefficient are activated. Now you can modify the basic rack profile.
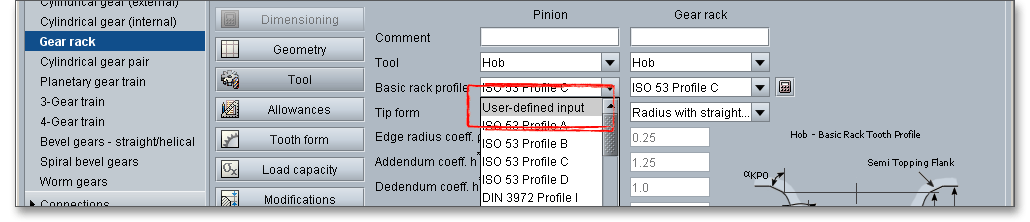
In case you use special tools, the eAssistant software offers an easy and comfortable solution. The basic rack profile can be determined by clicking the ‘Calculator’ button. Here you can change the tip circle and the root diameter for gear 1, gear 2 and gear 3. Confirm your entries with the button ‘OK’. The listbox for the basic rack profiles displays then ‘user defined input’. The modification of the tip diameter is set to ’0’.
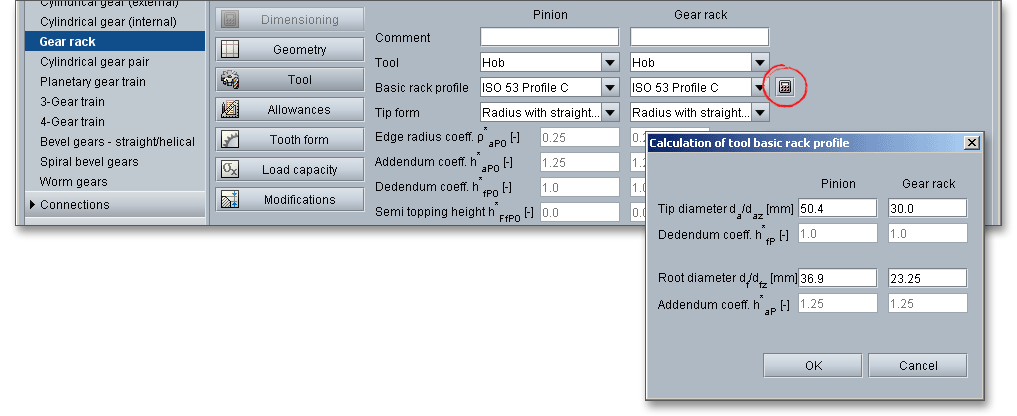
For the tip form you can choose between ‘Full radius’ and ‘Radius with straight line’. Normally ‘Radius with straight line’ is used.

With the definition of the semi topping flank, corresponding hobs can then be specified. These generate an addendum chamfer during the cutting process. The option ‘Topping’ allows to define the tip diameter directly with the dedendum coefficient of the tool, making it impossible to subsequently modifiying the tip diameter. The result, at the same time, will be tip diameter allowances analogous to the root diameter allowances directly from the tooth thickness allowances. The eAssistant 3D CAD plugins for various CAD systems support the function and the semi topping flank can be considered in the 3D CAD model.

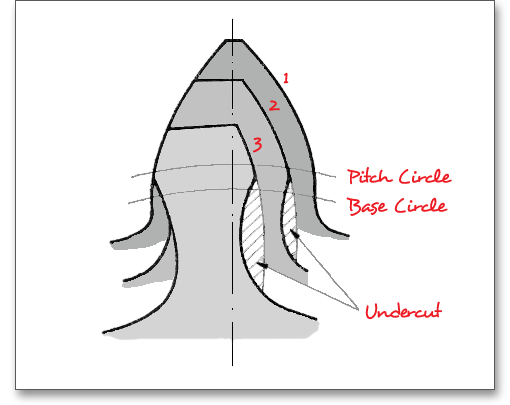
Undercut may be deliberately introduced to facilitate finishing operations. Undercut is the loss of profile in the vicinity of involute start at the base circle due to tool cutter action in generating teeth with low numbers of teeth. The protuberance cuts an undercut at the root of the gear tooth. The protuberance design is also used in some cases to permit the sides of gear teeth to be ground without having to grind the root fillet.
The following equation determines the amount of the protuberance. In case the height of the protuberance flank is given and not the amount of the protuberance, the amount of the protuberance may be calculated by this equation.
\[pr^{*}_{P0} = \frac {(h^{*}_{prP0} - \rho ^{*}_{aP0}\cdot (1-\sin (\alpha _{p})))\cdot \sin (\alpha _{n} - \alpha _{p})} {\cos (\alpha _{p})} + \rho ^{*}_{aP0} \cdot (1-\cos (\alpha _{n} - \alpha _{p})) \]
The following figure shows a representation:
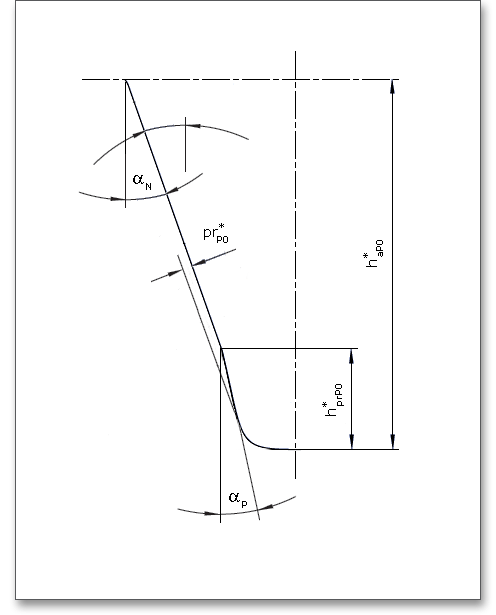
To avoid grinding steps, a deviation in the tooth root area of the profile is a common and allowed method. Because of a grinding stock allowance, an undercut must be allowed. Hence, a larger tooth root thickness is necessary. The following table shows some determination of the undercut dependent upon the module.
| Undercut \(s_{pr}\) for Ground Gears Dependent upon Module2
| |||||
| Module | Allowance | Size of | Protuberance | Addendum | Edge Radius |
| \(m\) | \(q\) | Undercut \(s_{pr}\) | \(pr^{*}_{P0}\) | \(h^{*}_{aP0}\) | \(\rho ^{*}_{aP0}\) |
| 2 | 0,160 | 0,100 | 0,260 | 2,900 | 0,500 |
| 2,5 | 0,170 | 0,110 | 0,280 | 3,625 | 0,625 |
| 3 | 0,180 | 0,120 | 0,300 | 4,350 | 0,750 |
| 4 | 0,200 | 0,140 | 0,340 | 5,800 | 1,000 |
| 5 | 0,220 | 0,160 | 0,380 | 7,250 | 1,250 |
| 6 | 0,240 | 0,180 | 0,420 | 8,700 | 1,500 |
| 7 | 0,260 | 0,200 | 0,460 | 10,150 | 1,7500 |
| 2 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag, Muenchen, Wien, 2nd ed. 2010, p. 68, table 2.1/2
| |||||
You can consider an allowance for the tooth flank. The tool provides an allowance \(q\) on the flank and/or root for the pre-cutting tool. The allowance is the smallest distance between the involutes and the pre-machining having the same root diameter. In case you select the tool basic rack profile with protuberance, the allowance refers to the tooth flank.
If the allowance of the tool basic rack profile is selected without protuberance, then tooth flank and tooth root get the allowance.
| Maximum Machining Allowances3
| |
| Allowance per Tooth Flank | Manufacturing Process |
| \(<\) 0.05 (0.10) mm | Finishing operation by cold rolling, gear shaving, honing, lapping |
| 0.05 to 0.5 (1.5) mm | Grinding, profile grinding, (honing) |
| \(>\) 0.5 mm, pre-cutting | Primary shaping, forming, cutting with geometrically determined edges except shaving, grinding and profile grinding in special cases |
| 3 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag, Muenchen, Wien, 1996, p. 638
| |
A manufacturing of work-pieces with accurate nominal dimensions is impossible. Hence, a deviation from the nominal size has to be allowed. For a lot of applications the gear and the pinion of a pair must be independently manufactured and meshed without any modifications. That means, the parts have to be separately replaceable. In addition to DIN 3961 for gear tolerances/gear qualities, DIN 58405 for precision engineering as well as ISO 1328 and ANSI/AGMA 2015 are available.
The choice of the right toothing quality is determined by economical aspects depending upon the intended purpose and manufacturing process. In all fields of gearing, the control of gear accuracy is essential. Several classes or grades of accuracy can be set. 12 grades (12 to 1) are defined according to DIN standards. High accuracy grades can be set for a long-life, high speed gears. Lower accuracy grades will cover medium or slow-speed grades. Accuracy grade ‘1’ describes the highest possible accuracy, ‘12’ a very low accuracy. The gear accuracy ‘1 to 4’ is mainly used for master gears, quality ‘5 to 12’ is used for gear wheels (figure from: Niemann, G.: Maschinenelemente, Vol. 2, Getriebe allgemein, Zahnradgetriebe-Grundlagen, Stirnradgetriebe, 1989, p. 73, figure 21.4/1).
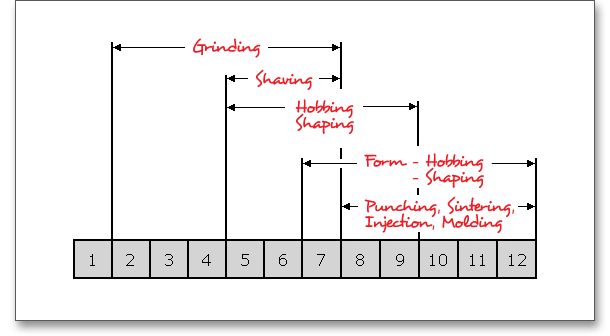
Select the appropriate quality between 1 and 12 by using the following listbox.
The following table provides some reference values for the selection of the quality, tolerances for gearings made of metal and plastics:
| Toothing Made of Metal4
| |||
| \(\nu \) | Machining | Quality | Tolerance Sequence |
| to m/s | of Tooth Flanks | (Accuracy) | DIN 3967 |
| 0.8 | Cast, raw | 12 | 2x30 |
| 0.8 | Rough-machined | 11 or 10 | 29 or 28 |
| 2 | Finish milled | 9 | 27 |
| 4 | Finish milled | 8 | 26 |
| 8 | Fine finished | 7 | 25 |
| 12 | Shaved or ground | 6 | 24 |
| 20 | Precision-ground | 5 | 23 |
| 40 | Precision-machined | 4 or 3 | 22 |
| 60 | Precision-machined | 3 | 22 or 21 |
| Toothing Made of Injection Molding Plastics
| |||
| Application | d | Quality | Tolerance Sequence |
| in mm | (Accuracy) | DIN 3967 | |
| Gearings with high requirements | to 10 | 9 | 27 |
| Gearings with high requirements | 10 to 50 | 10 | 28 |
| Gearings with normal requirements | 10 to 50 | 11 | 29 |
| Gearings with low requirements | to 280 | 12 | 2 x 30 |
| Toothing made of plastic manufactured by cutting
| |||
| Gearings with high requirements | to 10 | 8 | 25 to 27 |
| Gearings with high requirements | 10 to 50 | 9 | 26 to 28 |
| Gearings with normal requirements | to 50 | 10 | 27, 28 |
| Gearings with normal requirements | 50 to 125 | 11 | 27, 28 |
| Gearings with low requirements | to 280 | 12 | 28 |
| 4 from: Karl-Heinz Decker: Maschinenelemente: Gestaltung und Berechnung, 1992, p.
512, table 23.3
| |||
For the gear tolerances/gear qualities, DIN 58405 for precision engineering as well as ISO 1328 and
ANSI/AGMA 2015 are also available. For ISO 1328 and ANSI/AGMA 2015, two qualities can be selected in each
case. The first quality is comparable with the tolerances permitted according to DIN 3961, the second value
influences the radial composite deviation as well as the roll deviations.
The system for gearings is very similar to the DIN system of fits and tolerances. For the system of fits for gear transmissions letters are used to indicate the deviation from basic (nominal) size, a number defines the width. There are clearance fits for gearings, therefore, lower case characters ‘h’ to ‘a’ appear. If you select the entry ‘user defined input’, the input field for the tooth thickness allowances is enabled and you can define your individual values.
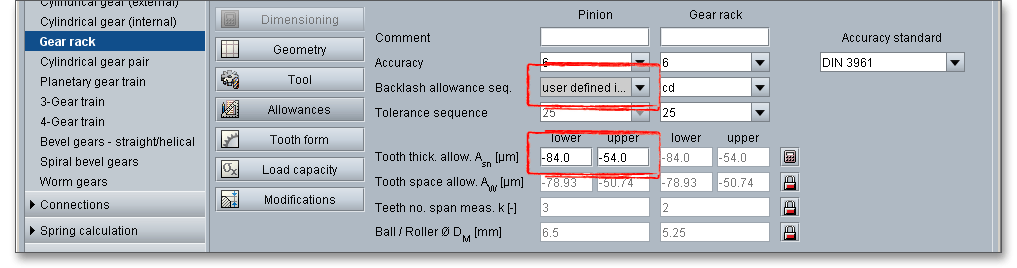
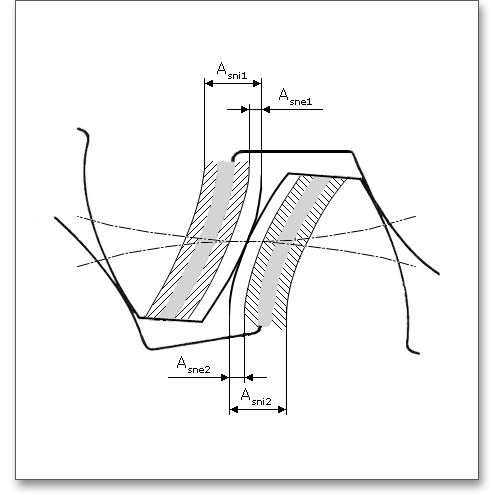
One of the most important criteria of gear quality is the specification and control of tooth thickness. The magnitude of tooth thickness and its tolerance is a direct measure of backlash when the gear is assembled with its mate. Dimensional changes, due to thermal expansion, do not allow a zero-backlash assembly. The tooth thickness allowance has to be determined that no jamming occurs. To prevent that jamming of gears during the operation, it is necessary to decrease tooth thickness by a minimum amount (\(A_{sne}\) and \(A_{sn}\)).
The tooth thickness allowances for teeth of external and internal gearings have to be negative. Then a backlash occurs (find more information on the backlash in section 10.4.8 ‘Backlash Normal Plane’). The eAssistant software offers the possibility to specify the tooth thickness allowances based on measured data or given test dimensions. Click on the ‘Calculator’ button.

A new window is opened.
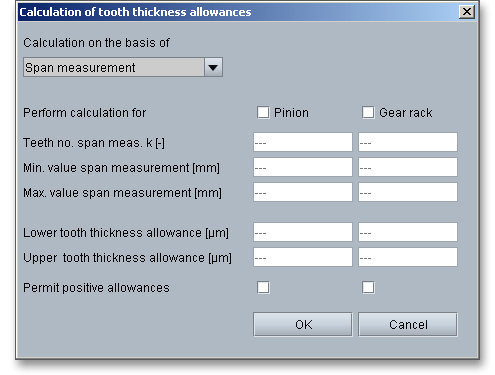
Activate pinion and gear rack and enter the input values. Confirm with the button ‘OK’. The ‘Lock’ button next to
the input field for the tooth space allowances is enabled. Now you can change the tooth space
allowances.
The tooth space allowance \(A_{W}\) is the difference between the actual dimension and the nominal dimension of the span measurement \(W{_k}\). The actual measurement of the span measurement gets smaller for external gears by negative allowances for a zero-backlash assembly. The upper and lower tooth space allowance are displayed as well. For an own input of the tooth thickness allowances, the tooth space allowances can be defined as well. The ‘Lock’ button next to the input field of the tooth space allowances is enabled. Therefore, you can change the tooth space allowances.
The tooth thickness of a gear may be measured directly with calipers or it may be determined indirectly by diameter pins. The sizing of gears may be controlled by double-flank composite checks and centre distance settings corresponding to maximum and minimum tooth thickness specifications. Different measurement methods are used:
In the following you get some information on the widely used measurement methods:
Span measurement \(W_{k}\) is the measurement of the distance across several teeth in a normal plane. As long as the measuring device has parallel measuring surfaces that contact on an unmodified portion of the involute, the measurement will be along a line tangent to the base cylinder. It is a widely used method for gauging the tooth thickness by using the span measurement. The tooth thickness of spur or helical gears is often measured with calipers. An advantage is that the dimensions can be influenced during the manufacturing.
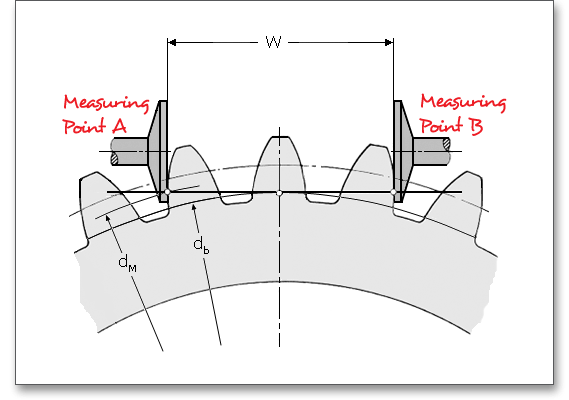
The calculation program determines the number of teeth for the span measurement (number of teeth across the span measurement has to be gauged). By using the ‘Lock’ button you are able to activate the input field and you can enter your own input value. If you click the button again, the previous input value appears.

The tooth thickness is often checked by measurement over pins \(M_{dR}\) or balls \(M_{dK}\). The pins or balls are placed in diametrically opposed tooth spaces (even number of teeth) or nearest to it (odd number of teeth). Measurement over pins is the measurement of the distance taken over a pin positioned in a tooth space and a reference surface. The reference surface may be the reference axis of the gear, a datum surface or either one or two pins positioned in the tooth space or spaces opposite the first. The measurement over pins is only used for spur gears and external helical gears. For the measurement values a distinction is made between:
For an external gear the measurement over balls \(M_{dK}\) is the largest outer measure. The two balls are placed in diametrically opposed tooth spaces. The balls have to be in the same plane perpendicular to a gear axis. For an internal gear (see figure: ‘Internal spur gear with odd number of teeth’) the measurement over balls is the smallest inner measure between the balls. \(D_{M}\) is the diameter of ball or pin. The internal gear is generally checked for tooth thickness with measuring pins, like the external gear. However, the measurement is made between the pins instead of over pins.
|
| Measurement over balls: External spur gear with evennumber of teeth |
|
| Measurement over balls: External spur gear with oddnumber of teeth |
|
| Measurement over balls: Internal spur gear with oddnumber of teeth |
The eAssistant software already specifies the diameter of ball or pin for the test dimensions. Enable the input field by clicking the ‘Lock’ button. Enter your own input value for the diameter. If you click on the button once again, the previous input value appears.

Please Note: In the calculation report you can find all results for the span measurement or measurement over
balls and pins in section ‘Test dimensions’.
The general purpose of backlash is to prevent gears from jamming and making contact on both sides of their teeth simultaneously. The center distance and the gear fits have an important influence on the backlash. The gear fit selection defines the tolerances of the centre distance with the backlash. The gear fit selection provides only one tolerance field. The allowances are indicated for the ‘JS’ field. These conform to the ISO basic tolerances. The backlash is dependent upon the tooth thickness allowances, the tooth space allowances and the centre distance. Hence, if you change the centre distance, then the backlash is changed, too.

Select the option ‘user defined input’ from the listbox. Now you are able to enter your own centre distance allowances. Confirm your entries with the Enter key. The backlashes are automatically determined.
The centre distance allowance \(A_{a}\) is the allowed deviation of the centre distance from the nominal centre distance. The allowances are indicated with \(\pm \) to get no improper major allowances from the nominal centre distances with gears having several axes.
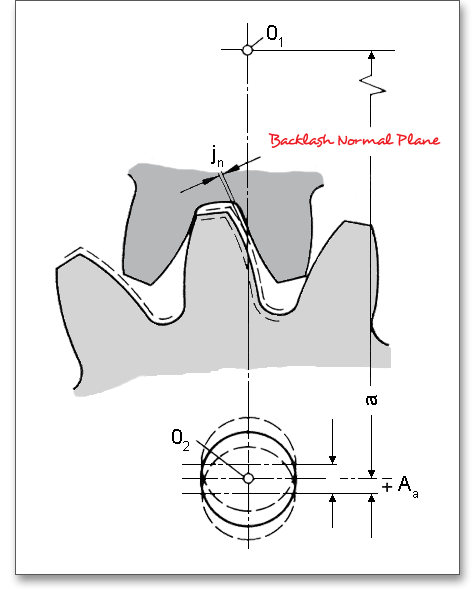
A gear fit has to be determined, so that two gears can be meshed. For that, a proper backlash must be provided for the mesh to avoid jamming of the gears. The eAssistant software offers three different backlashes: the backlash normal plane, the backlash pitch diameter and the radial backlash.
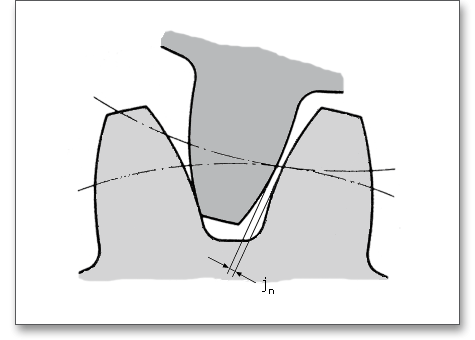
Besides errors in manufacturing and assembling, the variation in backlash will depend considerably on the tooth
thickness tolerances and centre distance of the gears. The DIN system represents a standard centre distance
and provides the backlash by changing the tooth thickness. The backlash between the meshing teeth adjusts
the deviations of the tooth thicknesses, centre distance and tooth form using the tooth thickness \(A_{sni}\) and tooth
space allowances \(A_{sne}\). The lowest tooth thickness allowance \(A_{sni}\) indicates the maximum backlash, the upper tooth
thickness allowance indicates the minimum backlash \(A_{sne}\). In addition to the tooth thickness allowance and centre
distance allowance, errors in profile and pitch are also factors to consider in the specification of the amount of
backlash.
Please note: The backlash depends also on thermal expansions, deformation of elementes and displacement
of casing. These impacts must be considered for the determination of the tooth thickness.
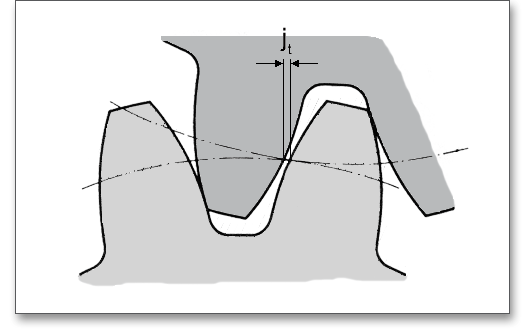
The backlash pitch diameter \(j_{t}\) refers to the backlash at the pitch circle. The backlash pitch diameter may be the length of the pitch circle arc in which the gear rotate against its mating gear.
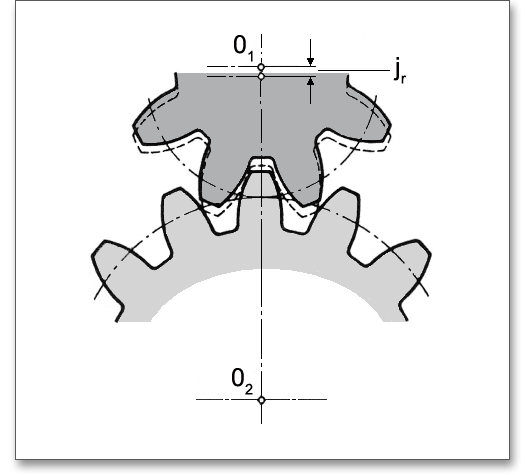
The radial backlash is the difference of the centre distance between the working condition and zero-backlash engagement. The radial backlash \(j_{r}\) matters especially for very small modules (m \(<\) 0.6 mm).
A special highlight of this calculation module is the presentation of the accurate gear tooth form with an animation and simulation of the tooth mesh. For the presentation you can select the lower, upper and mean allowances for the tooth thickness, tip diameter and centre distance. When you define the geometry for the gear pair, then you can have a look at the tooth form at any time. Click on the ‘Tooth form’ button and you get a general or detailed view of the tooth form. By clicking the ‘Geometry’ or ‘Tool’ button, you can open the main input masks of the calculation module again.
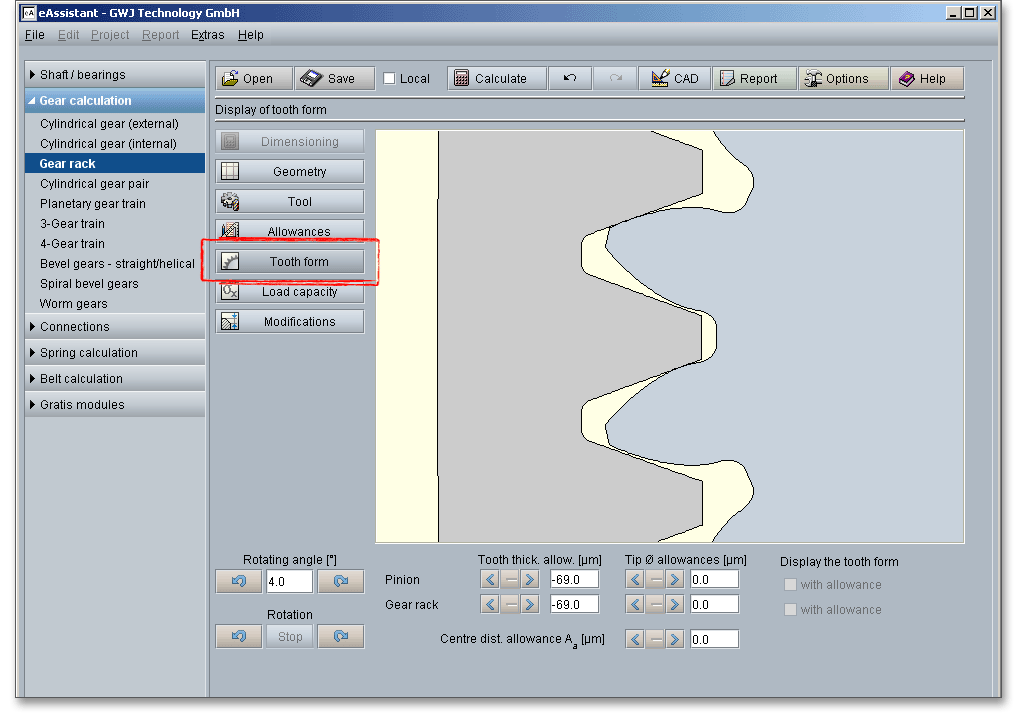
Please Note: Please keep in mind that all values are later taken over to the DXF output and CAD generation. In case you change the tooth thickness allowance or the centre distance allowance in the tooth form mask, then the last modification is taken over to the DXF output. The section 7.15 contains some helpful information on this function.
Enter an rotating angle for the rotation of gear pair.

|
| Rotation of the driving gear counter-clockwise |
|
| Rotation of the driving gear clockwise |
When you click on one of the two arrows, a continuous rotation of the spur gears occurs.

|
| Continuous rotation of the driving gear counter-clockwise |
|
| Continuous rotation of the driving gear clockwise |
|
| The rotation is stopped. |
Click on the ‘Detail view’ button and the tooth mesh is represented in detail. Now you can change the tooth thickness allowance, that is already given in the main mask for the ‘Allowances’, within the tolerance limit. All changes are displayed immediately. For the representation of the tooth mesh, select the lower, upper and mean tooth thickness allowances for pinion and gear rack.

Both arrows indicate the lower and upper allowance. The active input is grayed out and disabled. Click on the left arrow and you will get the representation for the lower tooth thickness allowance. The right arrow shows the representation for the upper tooth thickness allowance. The middle button displays the mean tooth thickness allowance. At the first start of the tooth form, you will get the mean tooth thickness allowance as a standard feature. The tooth thickness allowances can be defined between the lower and upper allowance.

Please Note: In case you have specified the lower and upper tooth thickness allowance for pinion and gear rack
in the input mask ‘Allowances’ by using the ‘Calculator’ button, then the manually defined values appear here as
lower and upper tooth thickness allowance.
Click the ‘Detail view’ button and the tooth mesh is represented in detail. Now you can change the tip diameter allowance for pinion and gear rack, that is already given in the main mask for the ‘Geometry’, within the tolerance limit. All changes are displayed immediately. For the representation of the tooth mesh, select the lower, upper and mean tip diameter allowances for pinion and gear rack.

Both arrows indicate the lower and upper allowance. The active input is grayed out and disabled. Click on the left arrow and you will get the representation for the lower tip diameter allowance. The right arrow shows the representation for the upper tip diameter allowance. The middle button displays the mean tip diameter allowance. At the first start of the tooth form, you will get the mean tip diameter allowance as a standard feature.

Please Note: In case you have specified the lower and upper tip diameter allowance for pinion and gear rack in
the input mask ‘Geometry’ by using the ‘Lock’ button, then the manually defined values appear here as lower
and upper tip diameter allowance.
Click on the ‘Detail view’ button and the tooth mesh is represented in detail. Now you can change the centre distance allowance, that is already given in the main mask for the ‘Allowances’, within the tolerance limit. All changes are displayed immediately. You can check the operation of the gears by using various centre distance settings.
For the representation of the tooth mesh, select the lower, upper and mean centre distance allowances for pinion and gear rack.

Both arrows indicate the lower and upper allowance. The active input is grayed out and disabled. Click on the left arrow and you will get the representation for the lower centre distance allowance. The right arrow shows the representation for the upper centre distance allowance. The middle button displays the mean centre distance allowance. At the first start of the tooth form, you will get the mean centre distance allowance as a standard feature.

Please Note: In case you have specified the lower and upper centre distance allowance in the input mask
‘Allowances’ by using the ‘User defined input’ option, then the manually defined values appear here as lower
and upper centre distance allowance.
Gears fail by tooth breakage, pitting as well as by scuffing. The strength is determined by the loads, the geometry of gearing as well as selected materials. The calculation of the load capacity is about the proof of the following strength factors that result from the above-mentioned forms of damage:
Tooth breakage is a fatigue failure. Pitting, scuffing or wear may weaken the tooth so that it breaks. The slow
progress of the fracture apparently causes the metal to break like brittle material. A tear or grinding notch may
cause a tooth breakage. Gear tooth fractures ordinarily start in the root fillet. The tooth breakage can destroy an
entire gearing and leads to a failure of the gearing. Sometimes a new tooth will break as a result of severe
overload or a serious defect in the tooth structure. According to DIN 3990, an operation with a reduced load is
possible after a tooth breakage, if just a small portion of a tooth broke off and the other parts of the gearing are
intact.
For a high load capacity of the tooth root, the following methods are advantageous: positive profile shift (for
small number of teeth), usage of hardened and tempered or case-hardened materials with larger load capacity
of the tooth root, larger root fillet, larger module
Pitting is a fatigue failure and is characterized by little bits of metal breaking out of the surface and thereby
leaving small holes or pits, so that oil seeps into the pits. This is caused by high tooth loads leading to excessive
surface stress, a high local temperature due to high rubbing speeds or inadequate lubrication. The
cracking of the surface develops, spreads and ultimately results in small bits breaking out of the tooth
surface. But it is often possible to get some years of service out of gears that have pitted rather
extensively.
For a high load capacity of the tooth flank, the following methods are advantageous: large number of teeth, positive profile shift (for small number of teeth), higher pressure angle, large hardness of tooth flank, nitriding, more viscous oil
Scuffing is a surface destruction and it can be caused by a lubrication failure. Tears and scratches appear on the rubbing surface of the teeth. This form of damage is called ‘scuffing’. The terms of ‘scuffing’ and ‘scoring’ are used interchangeably. Scuffing is an important form of damage leading to component replacements in lubricated mechanical systems. Compared with tooth breakage and pitting, it is not a fatigue failure, it can come very quickly. A short overload can lead to scuffing and the gearing fails. Scuffing is apt to occur when the gears are first put into operation because the teeth have not sufficient operating time to develop smooth surfaces. Due to the scuffing, the temperature, the forces and the noise increase, the gear teeth finally break off. The following factors may influence the occurrence of scuffing:
After the occurrence of scuffing, high-speed gears apt to additional dynamic forces that cause usually pitting or tooth breakage. The high surface temperature may cause a breakdown of the lubricating film. The following factors support scuffing:
For a high scuffing load capacity, the following methods are advantageous: E.P. oils (oil that contains chemical
additives), a careful running-in period of the gearing, low sliding velocity due to tip relief and a smaller
module
Please note: There are two different types of scuffing - cold and hot scuffing. Both types describe a
damage on the flank. The scuffing problem is not limited to high-speed gears. Scuffing can also
occur on slow-speed gears. The slow-speed scuffing is called cold scuffing and the high-speed hot
scuffing. Cold scuffing is not often observed. Hence, all further comments and information refer to hot
scuffing.
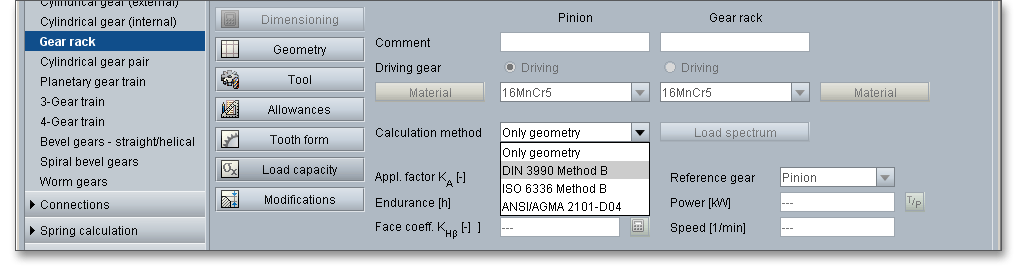
The calculation of load capacity of cylindrical gears is standardized according to DIN 3990, ISO 6336 and
ANSI/AGMA 2101-D04. The standards give different methods to calculate the load capacity in DIN 3990, ISO
6336 or ANSI/AGMA 2101-D04. The eAssistant software provides all calculations according to DIN 3990
Method B, ISO 6336 Method B and ANSI/AGMA 2101-D04. Hence, you can check the load capacity of tooth
root and tooth flank as well as the scuffing fast and easily. The scuffing safeties are determined according to the
integral and flash temperature method. The material properties, the endurance, face load factor, application
factor as well as the kind of lubrication and the selected lubrication are taken into consideration for
the calculation. There are extended input options to influence the number of load changes or the
roughness. A grinding notch can be integrated into the calculation and the mode of operation can be
selected.
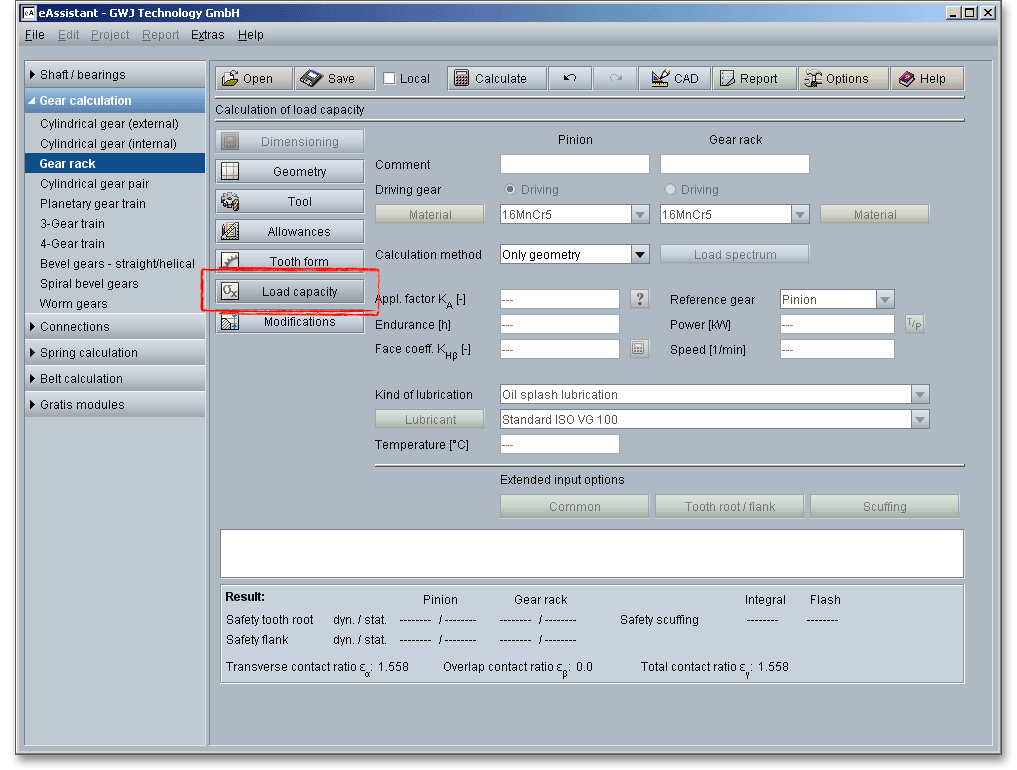
Click on the ‘Load capacity’ button to get to the calculation mask. You will notice that all input fields or listboxes are disabled. When you select the entry ‘DIN 3990 Method B’, ‘ISO 6336 Method B’ or ‘ANSI/AGMA 2101-D04’ from the listbox ‘Calculation method’, all input fields are enabled. In case you do not need the calculation for load capacity, the calculation can be disabled. Thus, the size of the calculation report becomes smaller.
You can add a description or a short comment to pinion and gear rack. The notes will appear later in the calculation report.

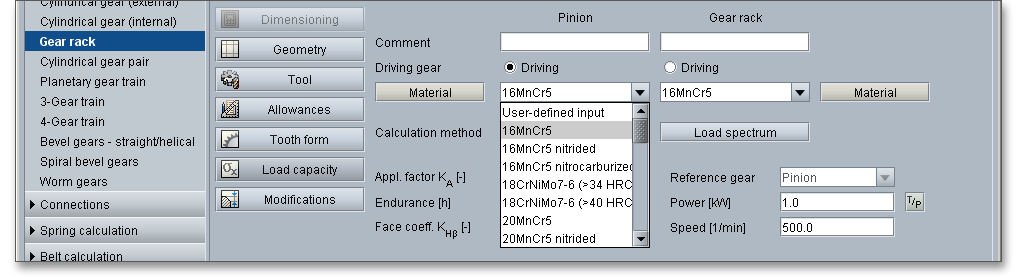
Select an appropriate material directly from the listbox or click on the button ‘Material’ to open the material database.
The material database provides some detailed information on the several kinds of material. If the listbox is active, the two arrow keys ‘Up’ and ‘Down’ of your keyboard allows you to search through the database, so you can compare the different values with each other.
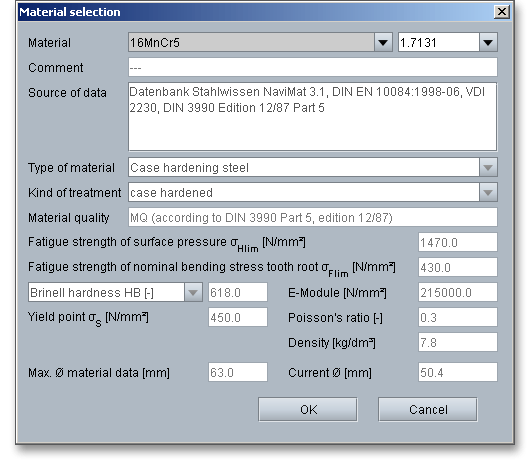
In order for gears to achieve their intended performance, life and reliability, the selection of a suitable material is
very important. Steel is the most common material that is used for gears. There are a number of steels used for
gears, ranging from plain carbon steels through the highly alloyed steels from low to high carbon
contents. The choice will depend upon a number of factors, including size, service and design.
For pinion and gear, the same hardened and tempered steel may be used. It has to be kept in
mind that unhardened gears with equal hardness should not be meshed with each other because
scuffing is apt to occur. A hardened or nidrided gear \(HRC > 50\) smoothes the tooth flanks of the hardened and
tempered mating gear, reduces the form deviations and increases the load capacity of the tooth
flank. For a mating of hardened gears, no hardness difference is necessary. The final selection of
the material should be based upon an understanding of the material properties and application
requirements.
Hardening and tempering differs from hardening by annealing at high temperatures. The temperature range for hardening and tempering ranges from \(400^{\circ }\) to \(700^{\circ }\)C while after hardening, parts are annealed at a low temperature. On the other hand, a distinction is made between the material. For hardening, steel contains more than 0.6 to 0.7% of carbon, for hardening and tempering less than 0.6% of carbon. However, there is no well-defined limit between hardening and tempering and hardening.
Steel casting: Steel casting belongs to the ferrous metals that include carbon (up to max. 2%) and are
poured into sand molds to produce several components. Due to a higher melting temperature,
steel casting is more difficult to cast than cast iron. Steel casting is cheaper than ground or forged
gears.
Steel: Steel is the most common material and is used for medium and high-loaded gears.
Nidrided steel: Nitriding is adding nitrogen to solid iron-base alloys by heating the steel in contact with
ammonia gas or other suitable nitrogenous material. This process is used to harden the surface of
gears.
Case-hardened steel: Case-hardened steel is a quality and high-grade steel with low carbon content.
Case-hardened steel is usually formed by diffusing carbon (carburization), nitrogen (nitriding) into the outer layer
of the steel at high temperature and then heat treating the surface layer to the desired hardness. When the steel
is cooled rapidly by quenching, the higher carbon content on the outer surface becomes hard while the core
remains soft and tough.
Blackheart malleable cast iron (pearlitic structure): Malleable cast iron is a heat-treated iron carbon alloy. Two
groups of malleable cast iron are specified, whiteheart and blackheart cast iron. Blackheart malleable cast iron
is used for parts with a complex shape, in which a high durability, shock resistance and good machining are
important. Malleable cast iron is used for smaller dimensions and has got a higher strength and toughness than
steel castings.
Cast iron with spheroidal graphite (pearlitic structure, bainitic structure, ferritic structure): Cast iron usually refers
to gray cast iron but identifies a large group of ferrous alloys that contain more than 2% of carbon. It is extremely
rare that the maximum carbon content is higher than 4.5%. Cast iron is a low-priced material. However, cast iron
has less toughness and ductility than steel. Cast iron with spheroidal graphite can be used for parts with higher
vibration stress.
Heat-treated steel: Hardening and tempering is a heat-treating technique for steels by quenching from the
hardness temperature and annealing at a high temperature so that the toughness is increased significantly. At
the same time, a higher elastic limit is reached. Annealing temperatures and times differ for different
materials and with properties desired, steel is usually held for several hours at about \(400^{\circ }\)C to \(700^{\circ }\)C. Some
steels have to be cooled very quickly (Annealing: in order to achieve the intended properties of work
pieces (e.g., desired strength or toughness), reheating of the work pieces to certain temperatures is
necessary.).
Gray cast iron: Gray cast iron is used for complex shapes and offers low cost and an easy machinability. It provides excellent damping properties but it is a disadvantage that the load capacity is very low.
Please Note: In case there is no material that will fulfill the design requirements, then simply define your individual material. Select the option ‘User defined input’ and all inputs and options are enabled and you can specify your individual material very easily. Your inputs will be saved to the calculation file.
Please be advised that changing the material will delete your defined inputs and you have to enter the inputs again.
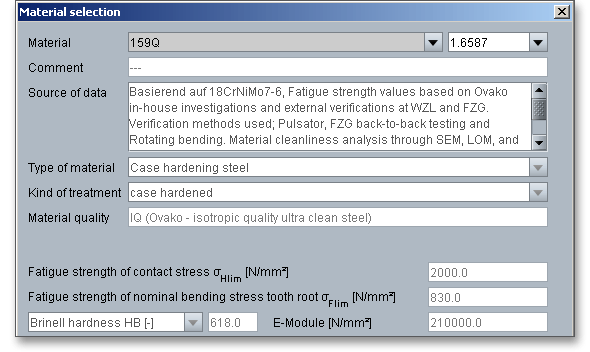
Ovako´s clean steels 159X and 159Q can be selected from the listbox. Both steels are based on the case-hardening steel 18CrNiMo7-6. Due to significantly lower levels of contamination, these steels have modified Woehler curves. Within the static strength, both steels are comparable to 18CrNiMo7-6. However, in the fatigue strength range the IQ-Steel 159Q (Isotropic Quality ultra clean steel) is designed to increase efficiency by 30 percent for the flank load capacity and 60 percent for the tooth root load capacity. The fatigue strength values are based on Ovako´s in-house investigations and external verifications at WZL of RWTH Aachen University and at the Gear Research Centre (FZG) of Technical University of Munich.
The BQ-Steel 159X (Bearing Quality clean steel) delivers slightly smaller performance gains compared to 18CrNiMo7-6 and can be taken to improve existing designs. The potential of the 159Q can be used particularly in new designs. It can be advantageous to focus on optimized scuffing load capacity. This can be achieved by increasing the number of teeth and simultaneously reducing the module. This generally results in better gear efficiency and lower power losses. These Ovako steels open up completely new design possibilities for gears and have a high potential for further increasing the performance of gears and gear components.
The calculation of load spectra is in accordance with ISO 6336, Part 6. The determination is based on the Palmgren-Miner rule and the load-dependent K-factors are calculated for each torque class. The safeties are determined by way of iteration until the sum of damage parts is obtained. This method, demanded by the wind energy industry, is very accurate. The linear damage accumulation model, which is also known as Palmgren-Miner’s rule, defines damage as the ratio of the number of cycles of operation to the number of cycles to failure at any given stress level.
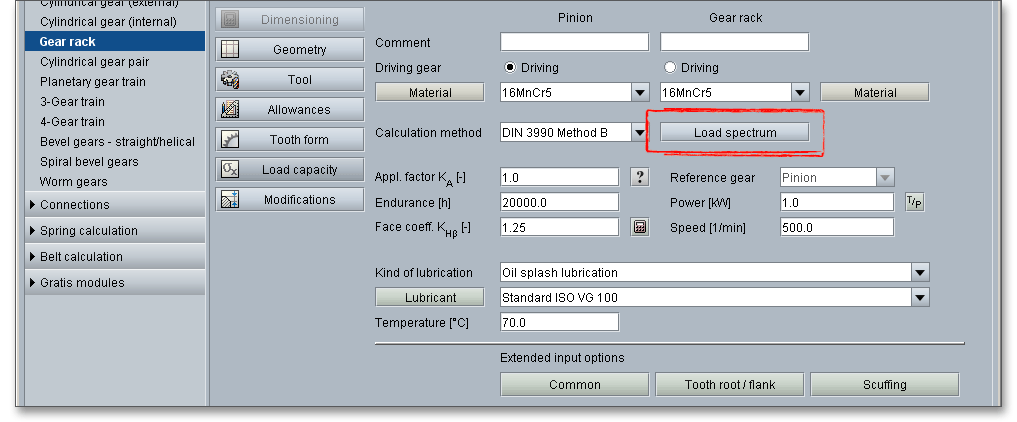
Click the button ‘Load spectrum’. Once the option ‘Use load spectrum’ has been activated, add any number of load spectra with time ratio, torque and speed. The load spectra can be entered manually or imported from files. The load spectra can be saved and loaded. To do this, use the two buttons ‘Open’ and ‘Save’.
The application factor \(K_{A}\) evaluates the external dynamic forces that affect the gearing. These additional forces are largely dependent on the characteristics of the driving and driven machines as well as the masses and stiffness of the system, including shafts and couplings used in service. Because scuffing is not a fatigue failure, the application factor shall consider the stronger influence of several load peaks during the calculation of the scuffing load capacity. Several load peaks affect directly only the flank temperature. Because of that, the same application factor \(K_{A}\) can be used for the calculation of the scuffing load capacity as well as of the load capacity of the tooth root and tooth flank. The application factor is determined by experience. An application factor of ‘1.0’ is best thought of a perfectly smooth operation. The following table gives some values according to DIN 3990.
| Application Factors \(K_{A}\) According to DIN 3990-1: 1987-125
| ||||
| Working Characteristics | Working Characteristics of the Driven Machine | |||
| of the Driving Machine | Uniform | Light shocks | Moderate shocks | Heavy shocks |
| Uniform | 1.0 | 1.25 | 1.5 | 1.75 |
| Light shocks | 1.1 | 1.35 | 1.6 | 1.85 |
| Moderate shocks | 1.25 | 1.5 | 1.75 | 2.0 |
| Heavy shocks | 1.5 | 1.75 | 2.0 | 2.25 or higher |
| 5 from: DIN 3990 Part 1, December 1987, p. 55, table: A1
| ||||
Please Note: You will find a ‘Question mark’ button next to the input field. Click on this button and the above-mentioned table opens. The ‘Question mark’ button is an additional feature and provides further information. You will find this button next to several input fields.

The face load factor takes into account the effects of the non-uniform distribution of load over the gear facewidth on the surface stress \(K_{H\beta }\), on the tooth root stress \(K_{F\beta }\) and on the scuffing \(K_{B\beta }\). The face load factor is determined according to DIN 3990, Part 1 Method B.

When you start the calculation module, the value ‘1.25’ is entered into the input field. In case you already use a defined face load factor, you can save the certain factor to a template file. Then the calculation module starts with the individual face load factor. When you click on the ‘Calculator’ symbol, the input mask for the face load factor opens. In the top input field ‘Face coeff.’ you can find the default value ‘1.25’. You will notice that the lower input fields and listboxes are disabled. By using the ‘OK’ button you can take over the default value to the main mask. There is a listbox next to the input field for the face load factor. When you open the listbox, the entry ‘DIN 3990 T1 Method B’ appears.

As soon as you select this entry from the listbox, the remaining input fields and listboxes are enabled. The face
load factor is determined automatically but you still cannot take over the value to the main mask. In order to take
over the calculated value, you have to add further inputs from the input mask for the face load factor. When the
button ‘OK’ is activated, then the determined face load factor can be confirmed with the button
‘OK’.
Please Note: However, there is the possibility to take over the value, determined according to DIN, to the main mask without changing the extensive settings. When you click on the ‘Calculator’ button next to the face load factor, the above-mentioned input mask opens. The face load factor \(K_{H\beta }\) is displayed in the input field. Open the adjacent listbox and select the entry ‘DIN 3990 T1 method B’. The face load factor is calculated but the button ‘OK’ is still disabled.
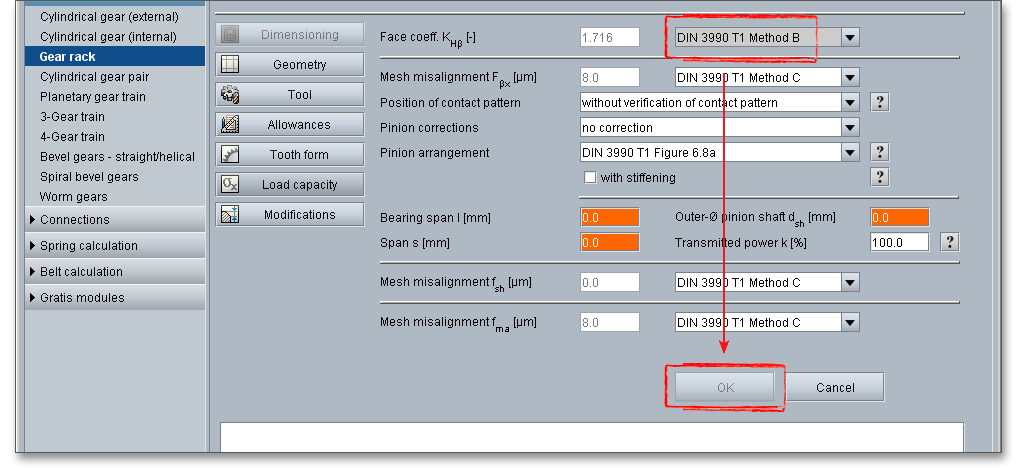
Open the listbox again and select the entry ‘User defined’. Now the ‘OK‘ button is enabled and you can take over the face load factor.
The path of teeth is marked by the path of tooth traces. The tooth trace is the section of a tooth flank with the reference surface. The mesh misalignment \(F_{\beta x}\) considers all influences of manufacturing, assembly and deformation that may intensify and compensate each other.
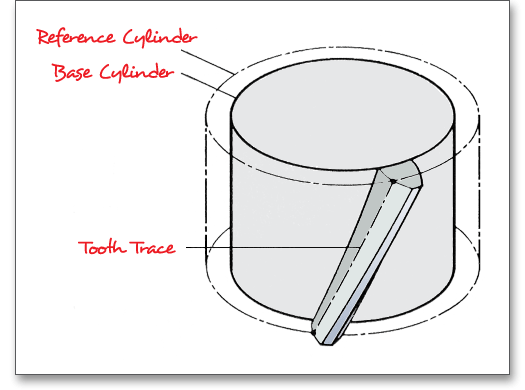
The mesh misalignment is determined according to DIN 3990, part 1 method C. Using this method, portions of the mesh misalignment are considered caused by a deformation of pinion and pinion shaft as well as manufacturing inaccuracies. \(F_{\beta x}\) consists of \(f_{sh}\) and \(f_{ma}\). \(f_{sh}\) is the mesh misalignment due to bending and torsion of the pinion and pinion shaft, therefore it is a mesh misalignment due to deformation. The mesh misalignment \(f_{ma}\) is a misalignment due to manufacturing inaccuracies and is dependent upon the gear accuracy and the facewidth of the gear.

Please Note: Select the entry DIN 3990 method B from the listbox for the face load factor, then the factor is determined according to DIN. The selection and input fields are enabled. User-defined inputs for the mesh misalignment are also possible.

The tooth contact pattern gives some insight into the required geometry and accuracy of gears. While rolling off each other, a tooth flank will not come into contact with every point of its mating flank. A tooth contact pattern is a representation of contact surfaces of two engaged tooth flanks of gear pair. Under operating conditions, an even load distribution over the facewidth and tooth depth is to be accomplished. For a contact pattern, a thin layer of a marking compound is applied to the flanks. After that, the gear pair is rotated as long as the tooth contact pattern appears. Then the gears are visually inspected to check the tooth contact pattern which is indicated by a light wear pattern on the mating tooth surfaces. The optimization of the contact pattern plays an important role for improving smoothness and quietness of operation. Click on the ‘Question mark’ button and you will get a representation of the contact pattern according to DIN 3990, Part 1.

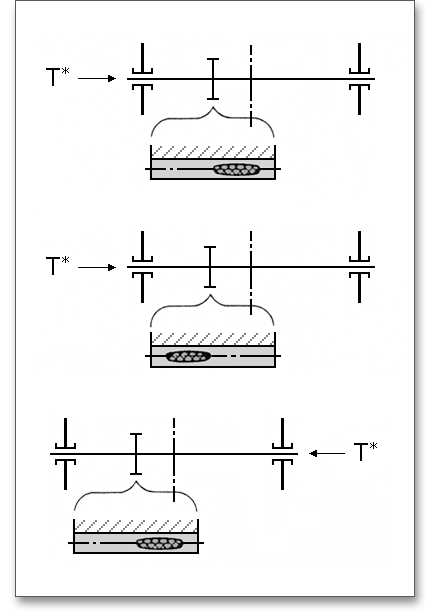
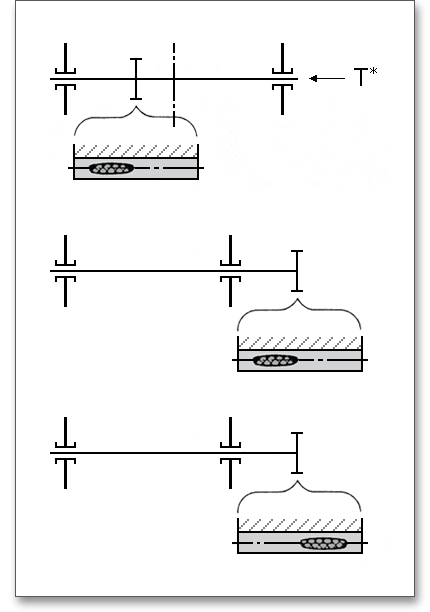
Errors in manufacturing and elastic deformations that may influence the load capacity can be adjusted by using intentional deviations from the involute (modification of the tooth depth) and theoretical tooth trace (modification of the facewidth). Lead crowning and end relief are the most important pinion corrections and are advantageous for a good load distribution over the facewidth of a gear. Due to lead crowning or end relief, a non-uniform load distribution can be reduced. The calculation program allows you to select one of the above-mentioned pinion corrections from the listbox.

Lead crowning is a common modification that results in the flank of each gear tooth having a slight outward bulge in its center area. A crowned tooth becomes gradually thinner towards the end of the teeth. The purpose of lead crowning is to ensure that manufacturing inaccuracies and deformations are adjusted under load and that the tooth ends are relieved. In general, lead crowning \(C_{c}\) is carried out symmetrically to the centre of the facewidth.
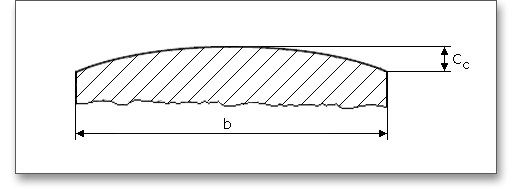
Due to mesh misalignments, an overloading of the tooth ends occurs. Therefore, this kind of pinion correction is used to protect the tooth ends against overloading. Generally, the size of the relief at both sides of the tooth flank is equal. If crown shaving and crown grinding are not possible, then end relief is recommended.
When \(d_{1}/d_{sh} \geq 1,15\), then stiffening is assumed; when \(d_{1}/d_{sh} < 1.15\), there is no stiffening; furthermore, scarcely any or no stiffening at all is to be expected when a pinion slides on a shaft and feather key or a similar fitting, nor when normally shrink fitted (DIN 3990, part 1, edition December 1987, Beuth Verlag GmbH Berlin, figure 6.8, p. 33).
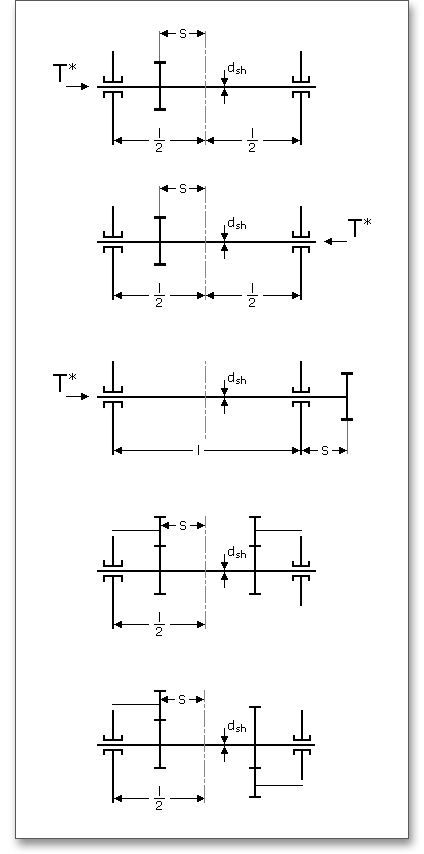
The transmitted power \(k\) is the percentage of the power which will be transmitted through the pinion tooth mesh, in the ratio of the full power which is transmitted through the pinion shaft. For example: The power input on a shaft is 10 kW. 60% is transmitted through the tooth mesh and the remaining 40% is transmitted to the end of the shaft. Now you have to define 6 kW for the pinion to dimension the gearing. To determine the face load factor, you have to enter 60% of the transmitted power because the stronger deformation of the shaft due to the full torque transmission (10 kW) is taken into consideration.

The inputs for the power, speed and torque apply for the appropriate gear that is selected in the listbox. For the
other gear, speed and torque are determined from the reference gear.
The power, torque and speed are dependent upon each other. Click on the adjacent button ‘T/P’ to switch
between the input for the torque and the input for the power. If you click on the ‘TP’ button, then you can enter
either the torque or the power. The values are converted. The description of the input field changes accordingly
into ‘Torque’ or ‘Power’.
Lubrication serves several purposes but its basic and most important function is to protect the sliding and rolling tooth surfaces from seizing, wear and friction. The friction of the tooth flank is responsible for flank wear, gear heating and gear noise. A reduced flank friction improves the efficiency that is dependent on the tooth load, circumferential velocity, gear quality and the surface condition of the tooth flanks. In order that the gearing should work properly, the selection of a lubricant is an important choice. A liquid lubricant is a good choice and can be easily introduced between the contacting surfaces. In addition, a lubrication has to reduce frictional heat and has to protect the surfaces against corrosion. The bearings and clutches in a gearing require also an appropriate lubricant. Therefore, the lubricant has to be suitable as well. Oil and greases are the most common lubricants. The compounding of oils provides a combination and generation of various properties. Oil offers a wider range of operating speeds than greases. They are easier to handle and are most effective. Special E.P. (extreme pressure) oils have been developed for slow-speed, highly-loaded vehicle gears. These oils develop chemical compounds on the contacting gear-tooth surfaces. Grease is a combination of liquid and solids. Grease has the advantage of remaining in place and not spreading as oil. It can provide a lubricant film at heavily loads and at low speeds.

For the selection of liquid lubricants applies: the smaller circumferential velocity and larger the contact pressure
as well as the roughness of tooth flanks, the higher the viscosity. A higher viscosity will result in a higher
hydrodynamic load capacity and an increased scuffing load limit where scratching and scuffing of the tooth
flanks occur (Muhs/Wittel/Jannasch/Vossiek: Roloff/Matek Maschinenelemente, 17th revised edition, published
by Vieweg, Wiesbaden 2005).
Please Note: If the viscosity is too low, the oil film will not be sufficiently formed and if the viscosity is too high,
the viscosity resistance will also be high and cause temperature rise. For higher speed, a lower viscosity oil
should be used and for heavy loads, a higher viscosity oil should be used.
Gears that are running primarily in a gearbox are lubricated with oil. A distinction is made between oil splash
lubrication and oil injection lubrication.
Oil splash lubrication: The oil splash lubrication is an easy, reliable and reasonable lubrication system.
It is a type of lubrication used in enclosed gear drives. In splash lubrication, the gear tooth dips
into a tray of lubricant and transfers the lubricant to the meshing gear as it rotates. As a result, oil
reaches all of the places where it is needed. The oil splash lubrication can be used for average speed
applications.
Oil injection lubrication: With the oil injection lubrication, the oil can be filtered, cooled and checked and the oil is
directly fed to the bearings. The amount of oil can be controlled according to the heat dissipation requirements.
The gearbox is used as an oil tank reservoir from which several units can be supplied. The oil is sprayed directly
by a pump injector into the mating surfaces.
Grease lubrication: The selection of the grease is dependent upon the circumferential velocity, the kind of application and the service temperature. A grease lubrication requires low maintenance and protects against contamination. Grease lubrication is suitable for any gear system that is opened or enclosed, so long as it runs at low speed. The grease should have a suitable viscosity with good fluidity especially in a enclosed gear unit. Click on the ‘Lubricant’ button and open database. The extensive database contains the lubricants including all detailed information about the oils and greases (e.g., density, viscosity, load stage of FZG test). Select ‘User defined input’ from the listbox to define your individual lubricant.
Click the corresponding button in the main screen of the load capacity to open the advanced input options. If you do not change any entries in the following screen, the calculation continues with the default input values.

If you do not change any entries in the following mask, the calculation continues with the default input values.
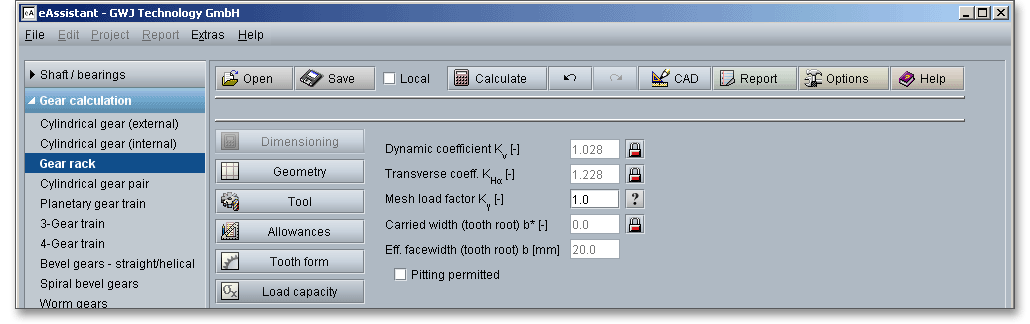
The dynamic coefficient \(K_{V}\) considers additional inner dynamic forces. Inner dynamic forces are caused by mesh
alignments, lead crowning, deformation of teeth, the housing, shafts and gear bodies as well as oscillation of the
wheel masses. As the circumferential velocity of the gear rim increases, the dynamic forces increase. The
forces decrease with an increasing load of the teeth. Click the ‘Lock’ button to change the dynamic
coefficient.
The transverse coefficients account for the effect of the non-uniform distribution of transverse load
between several pairs of simultaneously contacting gear teeth on the surface pressure (\(K_{H\alpha }\)), stress
leading to scuffing (\(K_{B\alpha }\)) and loading of the tooth root (\(K_{F\alpha }\)). Click the ‘Lock’ button to change the transverse
coefficient.
The mesh load factor takes into account an uneven distribution of the total circumferential force for gearings with
multiple transmission paths or for planetary gear trains with more than three planets. For transmission paths, the
total circumferential force is distributed to several mesh. For gearings without transmission paths, the value is
set at ‘1.0’.
When the facewidth of pinion and gear is not equal, then a maximum overhang of ‘1 x m’ at each
tooth end is assumed as a carried width. Unhardened portions of surface-hardened gear tooth
flanks (including transition zone) consider only 50% as the carried width. However, if it is foreseen
that because of crowning or end relief the contact does not extend to the end of face, then the
smaller facewidth shall be used for both pinion and gear. Click the ‘Lock’ button to change the carried
width.
In specific cases, the development of pits on the gear flank is allowed. Use this option to permit several pits. In general, initial pitting is considered normal and is not a cause for concern. In particular, case-hardened and nitrided gears usually has the tendency to pit near the tooth root and lead eventually to fatigue breakage. Here an individual assessment is necessary. In some cases (aerospace industry), pits are absolutely not permitted. For turbo transmissions, pits may lead to oscillations and increased additional dynamic forces.
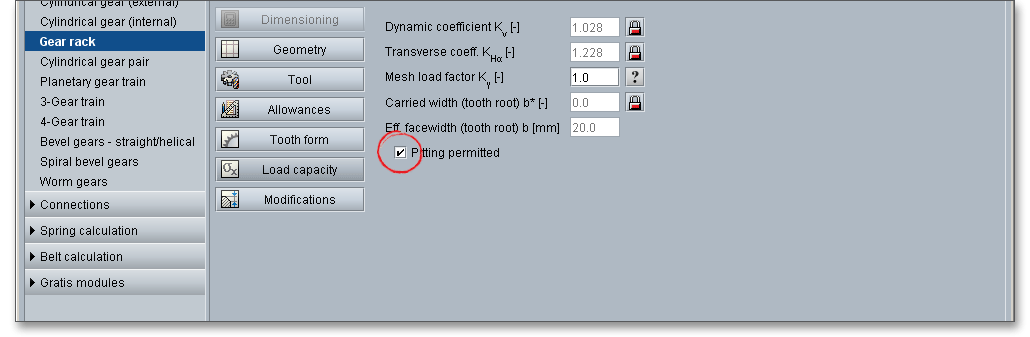
The main mask of the load capacity provides the ‘Tooth root/flank’ button, click on that button and the extended input options appear. If you do not change any inputs in the following mask, then the default input values are used.

The surface roughness of the tooth flanks influences the load capacity of the tooth flanks. The average
roughness \(R_{z}\) is the arithemitc average of five individually measured roughness values. The input of the roughness
occurs for root and flank of pinion and gear. The right choice of the surface roughness is determined by
economical aspects depending upon the intended purpose and manufacturing process. A fine surface can be
very expensive because of the high manufacturing costs. A surface that is too rough may not fulfill the required
functionality.
A grinding notch may significantly reduce the fatigue strength and a tooth breakage can occur due to a grinding notch.
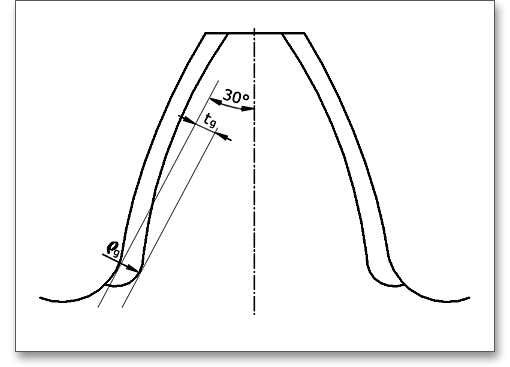
Shot-peening can be used to increase the fatigue strength of gears that are damaged by a grinding notch. A
careful grinding of the notch is basically suitable. Click the question mark button to open the representation of
the grinding notch.
The hardening depth is significantly for the pitting load capacity and is determined by the depth of surface layer heated to hardening temperature, the hardenability of the material and the effect of the quenching method. Case-hardening: Steels get their specific features by case-hardening. This combined heat treatment process consists of the following subprocesses:

Please Note: The calculation module determines the optimal hardening depth automatically, but the hardening depth can be defined also individually. If the individual hardening depth is smaller than the optimal hardening depth, then the fatigue strength is reduced accordingly. The determination of the optimal hardening depth and reduction of fatigue strength with reduced hardening depth is based on: ‘Tobie, Thomas: Zur Gruebchen- und Zahnfusstragfaehigkeit einsatzgehaerteter Zahnraeder, Dissertation Technische Universitaet Muenchen (Lehrstuhl fuer Maschinenelemente, Forschungsstelle fuer Zahnraeder und Getriebebau) 2001, Section. 10.3: Eingliederung der Versuchsergebnisse in das Rechenverfahren nach DIN 3990’.
The technology factor \(Y_{T}\) considers the change of the strength of the tooth root by machining process.
\[\sigma _{Flim} = \sigma _{Flim0} Y_{T}\]
| \(\sigma _{Flim0}\) | Fatigue strength of the tooth root from material data |
| \(\sigma _{Flim}\) | Fatigue strength of the tooth root with influence of the technology factor |
| \(Y_{T}\) | Technology factor (see following table) |
| Technology Factor \(Y_{T}\) According to Linke6
| |
| Kind of Manufacturing of the Tooth Root | Technology Factor \(Y_{T}\) |
| Shot peening: | 1.2 to 1.4 |
| Applies for case-hardened or carbonitrided gears; not ground in the hardened layer |
|
| Rolling: | 1.3 to 1.5 |
| Applies for flame and induction hardened gears; not ground in the hardened layer |
|
| Grinding: | General: 0.7 |
| Applies for case-hardened or carbonitrided gears | for CBN grinding wheel: 1 |
| Shape cutting: | 1 |
| Does not apply for ground gears |
|
| 6 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser Verlag
Muenchen Wien, 1996, p. 320, table 6.5/6
| |
Click the ‘Question mark’ button to open the tables for the technology factor and mode of operation factor.
The fatigue strength of the tooth root \(\sigma _{Flim}\) is corrected with the influence of the mode of operation.
\[\sigma _{Flim} = \sigma _{Flim0} Y_{A}\]
| \(\sigma _{Flim0}\) | Fatigue strength of the tooth root from material data |
| \(\sigma _{Flim}\) | Fatigue strength of the tooth root with influence of the mode of operation factor |
| \(Y_{A}\) | Mode of operation factor (see following table) |
The following reference values can be used for the mode of operation factor \(Y_{A}\). DIN 3990 specifies identical values for swelling and alternating load.
| Mode of operation factor \(Y_{A}\) according to Linke7
| ||
| Mode of Operation | Mode of Operation Factor \(Y_{A}\) | Direction of Load |
| Swelling | 1 | 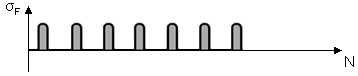 |
| Alternating | 0.7 | 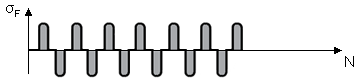 |
| Oscillating | 0.85 - 0.15 \(\frac {lgN_{rev}}{6}\) (for \(1\leq N_{rev} \leq 10^{6}\)) 0.7 (for \(N_{rev} > 10^{6}\)) | 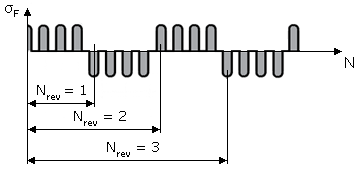 |
| Please Note: \(N_{rev}\) = Number of load direction changes during operation time
| ||
| 7 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser Verlag
Muenchen Wien, 1996, p. 321, table 6.5/7
| ||
The scuffing load capacity offers different extended input options. Click on the ‘Scuffing’ button and the extended input options appear.
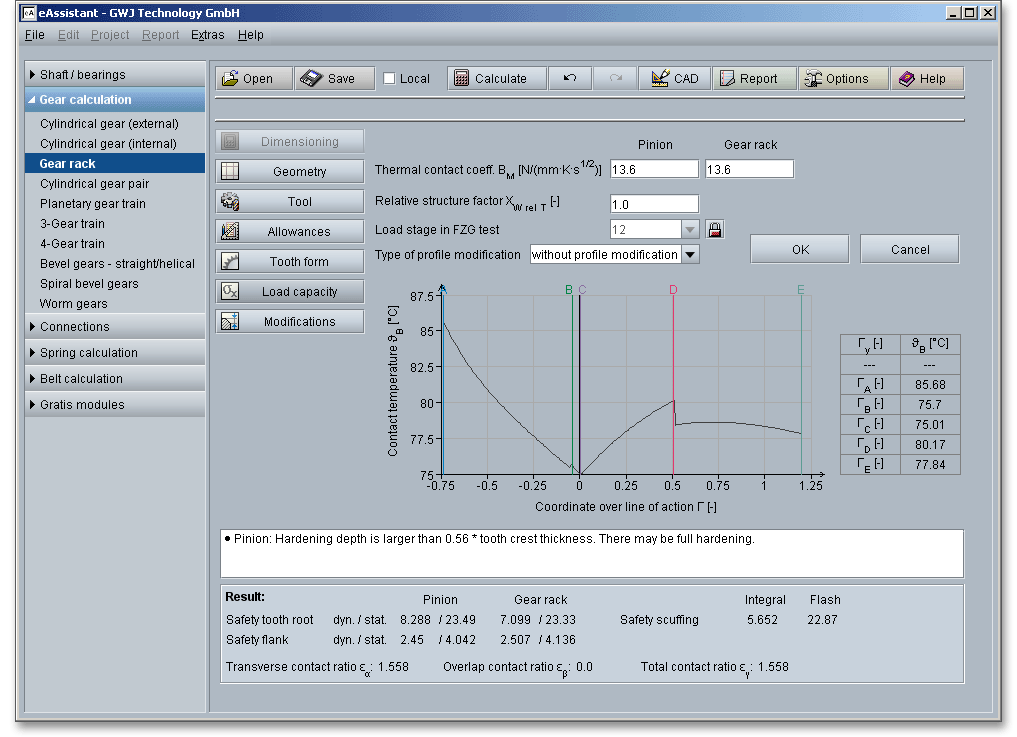
The thermal contact coefficient \(B_{M}\) is required for the determination of the flash factor. The flash factor considers the influence of the material properties of gear and pinion on the flash temperature.

The relative structure factor \(X_{WrelT}\) is primarily intended to take into account influence of the material properties on the scuffing load capacity and is determined by:
\[X_{WrelT} = \frac {X_{W}}{X_{WT}}\]
| \(X_{W}\) | The lower table provides the empirically determined relative structure factor. |
| \(X_{WT}\) | The relative structure factor for the test gears that are used for the determination of the scuffing |
| temperature. \(X_{WT}\) = 1.0 for the FZG gear test. |
| Material/Heat Treatment | Structure Factor \(X_{W}\) |
| Through-hardened steel | 1.00 |
| Phosphated steel | 1.25 |
| Copper plated steel | 1.50 |
| Bath and gas nitrided steel | 1.50 |
| Hardened carburized steel, with austenite content: | |
| - less than average | 1.15 |
| - average | 1.00 |
| - greater than average | 0.85 |
| Austenitic steel (stainless steel) | 0.45 |
| 8 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl
Hanser Verlag Muenchen Wien, 1996, p. 367, table 6.5/16
| |
Because scuffing is not a fatigue failure, a standard FZG gear test was developed to determine the scuffing load capacity of a lubricant under certain operating conditions. The gear test, known as FZG gear test (Institute for Machine Elements Gear Research Center, University Munich, Germany), is a standardized method according to DIN 51354. At the FZG, the different influences on scuffing are extensively investigated. The test is performed on a standard FZG test machine using standard test gears. Standardized, case-hardened and ground spur gears with a large one-side profile shift are used. The load is increased gradually on a FZG gear test rig with defined technical parameters. There are 12 load stages and the gears are inspected for scuffing after every load stage. Finally, the load stage is determined where scuffing of the gear teeth occurs and where the flank area is damaged by scratches. The higher the load stages, the better the industrial gear lubricants resistance to scuffing.
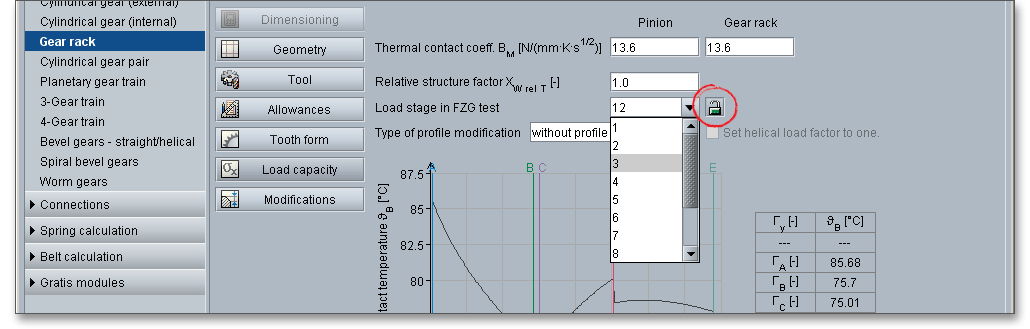
For high-duty gearings, it is possible to change the theoretical involute. Using the listbox to define the type of profile modification. You can select the following options:

The force distribution factor \(X_{\Gamma }\) evaluates the influence of the force distribution over several pairs of meshing teeth. A polygon-like shape over the line of action represents the progress of the force distribution factor. The values of the points A and E depend upon the type of profile modification. According to DIN 3990 (see Part 4, p. 17), the force distribution factor is as follows:
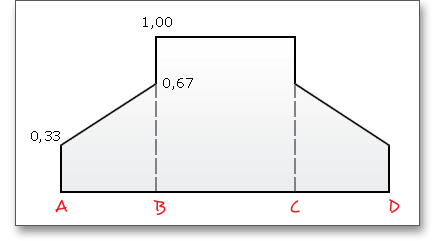
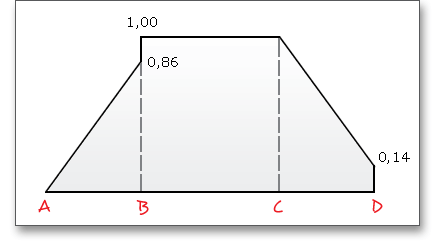
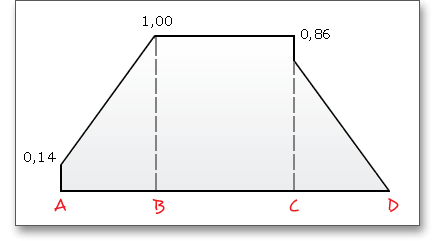
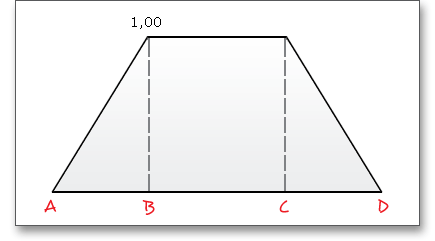
The contact temperature varies along the path of contact due to the progress of the flash temperature.
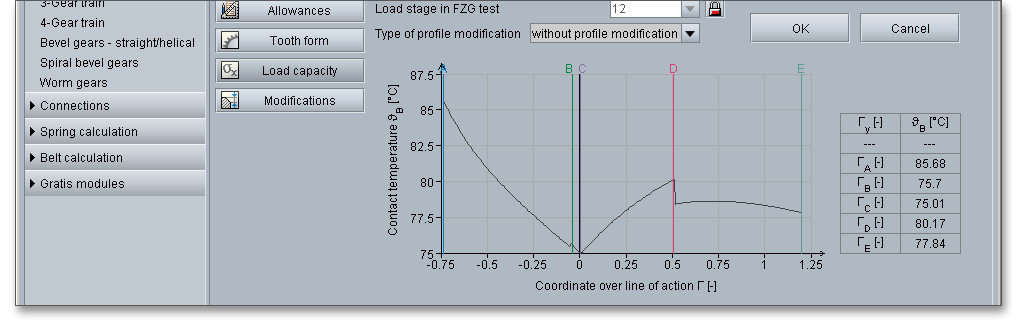
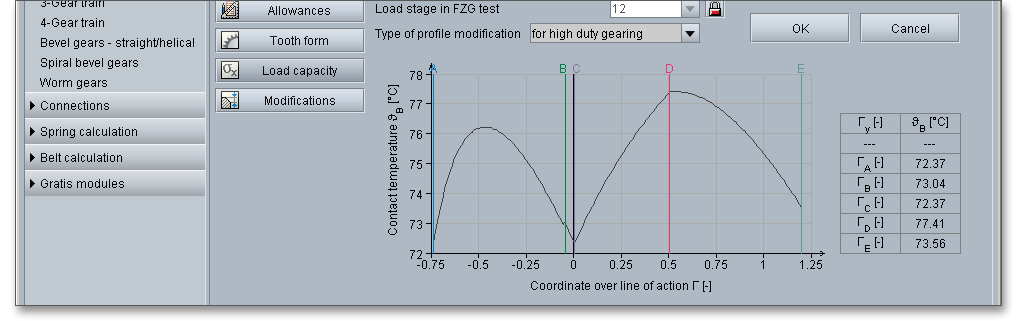
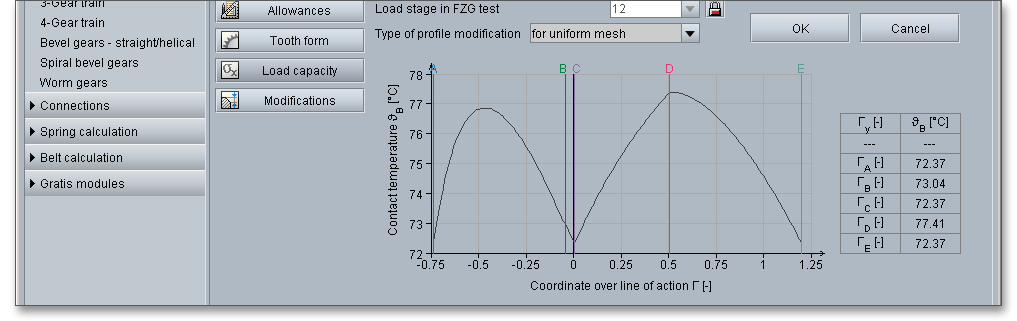
High surface temperatures due to high loads and slidings speeds can cause a lubricant film breakdown. Because of that, there are two calculation methods in ISO/TR 13989 that are based on different criteria for the development of a damage. The eAssistant software provides both the integral temperature method and flash temperature method:
The flash temperature is the temperature at which a gear-tooth surface is calculated to be hot enough to destroy the oil film and allow instantaneous welding at the contact point. The contact temperature \(\vartheta _{B}\) in any point of contact \(Y\) results from the sum of the bulk temperature \(\vartheta _{M}\) and the flash temperature \(\vartheta _{fla}\):
\[\vartheta _{B} = \vartheta _{M} + \vartheta _{fla}\]
According to the flash temperature method, there is no scuffing as long as the contact temperature \(\vartheta _{B}\) (as the sum of bulk temperature \(\vartheta _{M}\) and flash temperature \(\vartheta _{fla}\)) does not exceed the scuffing contact temperature in all points of contact. The scuffing temperature \(\vartheta _{S}\) to be a characteristic value for the material-lubricant-material system of a gear pair, to be determined by gear tests with the same material-lubricant-material system.
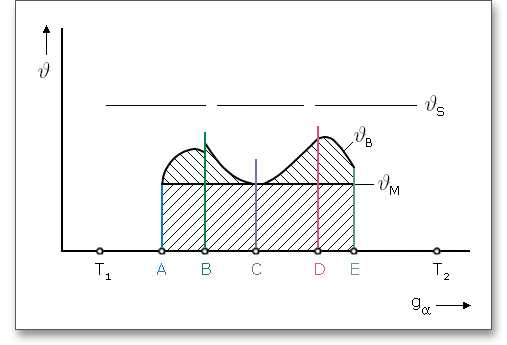
Please note: Points A to E mark the important points from the beginning to the end of the mesh.
The safety against scuffing \(S_{B}\) is determined according to the flash temperature method:
\[S_{B} = \frac {\vartheta _{S} - \vartheta _{oil}}{\vartheta _{Bmax} - \vartheta _{oil}} \geq S_{Bmin}\]
| \(\vartheta _{Bmax}\) | Maximum contact temperature along the path of contact |
| \(\vartheta _{oil}\) | Oil temperature before reaching the mesh |
| \(\vartheta _{S}\) | Scuffing temperature |
The safety factor \(S_{Bmin}\) is dependent on whether the gearing is put into operation after a good running-in period. With
a careful running-in period, there is no scuffing damage up to \(S_{Bmin} \approx 1\). Without a running-in period, there is no scuffing
up to \(S_{Bmin} \approx 3\) (according to Linke).
According to the integral temperature method, scuffing occurs when the integral temperature exceeds the scuffing integral temperature. The scuffing integral temperature is assumed as a characteristic value for the material-lubricant-material system of a gear pair and is determined from gear tests. The scuffing safety according the integral temperature method \(S_{intS}\) is calculated as follows:
\[S_{intS} = \frac {\vartheta _{intS}}{\vartheta _{int}} \geq S_{Smin}\]
| \(\vartheta _{intS}\) | Scuffing integral temperature |
| \(\vartheta _{int}\) | Integral temperature |
As uncertainties and inaccuracies in the assumptions cannot be excluded, it is necessary to introduce a safety factor. According to Linke, the following reference values can be used:
| \(S_{intS} < 1.0\) | In all probability, scuffing damages are expected to occur. |
| \(1.0 \leq S_{intS} \leq 2.0\) | For a careful running-in period of the gearing, good contact pattern and real assumed |
| loads, there are no scuffing damages to be expected. |
| \(S_{intS} > 2.0\) | There is no risk of scuffing. |
In addition to DIN 3990 Method B, it is possible to calculate the load capacity of tooth root and tooth flank according to ISO 6336 (2008) Method B. Select the ISO 6336 Method B from the listbox and the input fields are enabled.
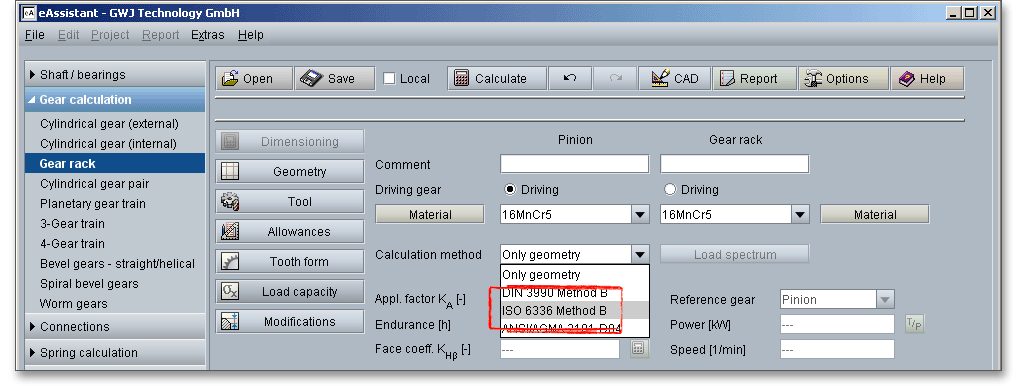
There is a strong similarity between the DIN 3990 standard and the ISO 6336 standard and most parts of the
load capacity calculation according to ISO 6336 correspond to DIN 3990. In fact, the ISO 6336 evolved from the
DIN 3990 standard. There are factors that influence the tooth root stress and tooth flank strength, but the
differences are minor and the influence on the safety of root, flank and scuffing is very low. One large difference
is the calculation of the helix angle factor \(Z_{\beta }\) as well as the calculation of the long life factors (\(Z_{NT}\) and \(Y_{NT}\)) for the tooth
root stress. Another difference between DIN 3990 and ISO 6336 is the critical stress point on the root fillet. ISO
6336 uses the tangency point of a \(60^{\circ }\) angle as the most critically stressed point on the root fillet for
internal gears. The DIN 3990 standard uses the tangency point of a \(30^{\circ }\) angle as the critical stress
point on the root fillet for external and internal gears as the basis for the calculation of the load
capacity.
The long life factor \(Y_{NT}\) accounts the higher tooth root stress and the long life factor \(Z_{NT}\) accounts the higher contact stress including static stress, which may be tolerable for a limited life (number of load cycles). The factors mainly depend on the quality of the material, heat treatment, number of load cycles as well as notch sensitivity, surface conditions and gear dimensions. The life factors \(Y_{NT}\) and \(Z_{NT}\) can be read from the following graph for the static and reference stress as a function of material and heat treatment.
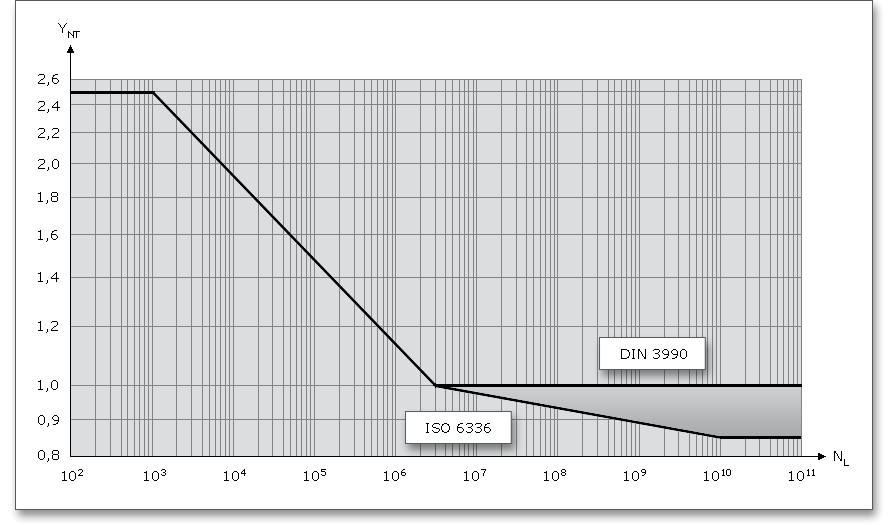
Long life factor \(Y_{NT}\):
With optimum lubrication, material and manufacturing \(Y_{NT}\) = 1.0 may be used for the number of load cycles \(N_{L} = 3 \cdot 10^{6}\). For
static stresses \(N_{L} \leq 10^{3}\), the long life factor is 2.5.
Long life factor \(Z_{NT}\):
With optimum lubrication, material and manufacturing \(Z_{NT}\) = 1.0 may be used for the number of load cycles \(N_{L} = 5 \cdot 10^7\). For
static stresses \(N_{L} \leq 10^{5}\), the long life factor is 1.6.

There are significant differences in the calculation of the life factors \(Y_{NT}\) and \(Z_{NT}\) when comparing DIN 3990 and ISO 6336. Values appropriate to the relevant number of load cycles, \(N_{L}\), are indicated by the S-N curve (also known as a Woehler curve). The S-N approach is different. The long life factor for the load capacity of the tooth root approaches 1.0 for the range of long life (depending on the material, usually at \(3 \cdot 10^6\) load cycles). In DIN 3990, the life factor remains 1.0 for higher number of load cycles. According to ISO 6336, the factor for materials decreases from 1.0 to 0.85 at \(10^{10}\) load cycles. Only after that, the factor remains 0.85 at \(10^{10}\) load cycles. For gears in the long life range, the calculations according to ISO 6336 result in significantly smaller safeties (15% lower) for tooth root and tooth flank. This also applies for the long life factor for flanks. Use the ‘Lock’ button to modify the long life factors \(Y_{NT}\) and \(Z_{NT}\). The input fields are enabled and you can define your own value for the factors. Please remember to keep the modified input field open or the default values will be used again.
Another difference between ISO and DIN is the determination of the mesh stiffness \(c_{\gamma }\). The mesh stiffness is
needed for the calculation of the face load factor \(K_{H\beta }\). The factor \(K_{H\beta }\) takes into account uneven distribution of load over
the facewidth due to mesh misalignment caused by inaccuracies in manufacture and elastic deformations. For
the calculation of the face load factor, ISO 6336 uses a mesh stiffness \(c_{\gamma }\) that is reduced by 15% in comparison to
the mean stiffness the DIN 3990 use for the calculation of \(K_{H\beta }\). This results in slightly lower face load
factors.
If the rim thickness is too thin and not sufficient to provide full support for the tooth root (e.g., for planetary gear
trains or internal gears), then this can be accounted for by the rim thickness factor \(Y_{B}\). \(Y_{B}\) is expressed as a function
of the tooth depth for external gears and as a function of the normal module for internal gears. The load capacity
decreases with a gear rim thickness \(s_{R} < 1.2 \cdot h_{t}\) for external gears or \(2.8 \cdot m_{n}\), for internal gears \(s_{R} < 3.5 \cdot m_{n}\) (ISO 6336 Edition 2006 - Was ist
neu?: Dr.-Ing. R. Hess, Dipl.-Ing. B. Kisters, A. Friedr. Flender AG, Bocholt, Tagungsbeitrag Dresdener
Maschinenelemente Kolloquium 2009).
Another difference is the determination of the helix angle factor \(Z_{\beta }\). Independent of the influence of the helix angle on the length of path of contact, this factor accounts for the influence of the helix angle on the load capacity of the tooth flanks, allowing for such variables as the distribution of load along the lines of contact. \(Z_{\beta }\) is dependent only on the helix angle, \(\beta \). The given formulae for the determination of the helix angle factor are different in DIN 3990 and ISO 6336. DIN 3990 gives the following formular to calculate the helix angle factor (\(\beta \) is the helix angle at reference circle):
\[Z_{\beta } = \sqrt {\cos \beta }\]
In ISO 6336, the helix angle factor is defined as follows:
\[Z_{\beta } = \frac {1}{\sqrt {\cos \beta }}\]
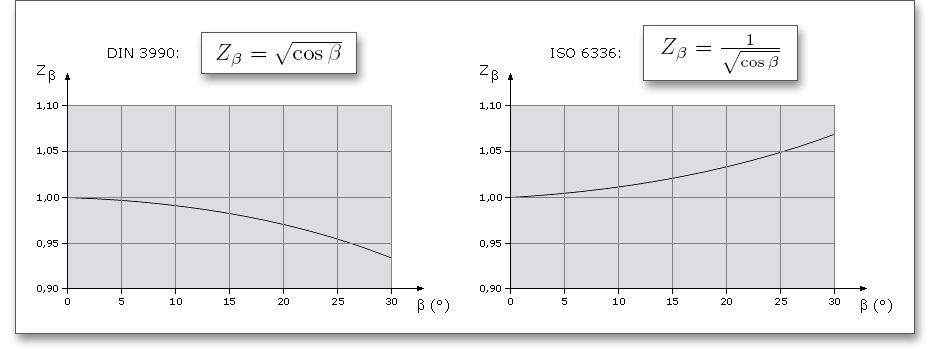
The work hardening factor \(Z_{W}\) has been revised in ISO 6336. This factor is used to take into consideration the
Hertzian pressure which serves as a basis for the calculation of the load capacity of the tooth flanks. The work
hardening factor accounts for the increase in surface durability due to meshing a steel gear with a hardened
or substantially harder pinion with smooth tooth flanks. In DIN 3990 and the previous version of
ISO 6336, the work hardening factor was dependent solely on the flank hardness of the softer
gear.
The increase in the surface durability of the soft gear depends not only on any work hardening of this gear, but
also on other influences such as flank surface roughness. In addition, the influence of the surface roughness is
addressed in ISO 6336. Tooth flank curvature, pitch line velocity and lubricant viscosity are taken into account in
the calculation. The work hardening factor is reduced for gears with hard, rough surface. Gear teeth with rough
surfaces may wear a softer mating teeth. Wear of the surface is not covered by ISO 6336. Especially for rough
pinion surfaces, values of \(Z_{W}\) < 1 may be evaluated. As in this range effects of wear can limit the surface
durability, \(Z_{W}\) is fixed at \(Z_{W}\) = 1.0 (ISO 6336 Edition 2006 - Was ist neu?: Dr.-Ing. R. Hess, Dipl.-Ing. B.
Kisters, A. Friedr. Flender AG, Bocholt, Tagungsbeitrag Dresdener Maschinenelemente Kolloquium
2009).
ISO 6336 does not provide a calculation method for scuffing. For the safety against scuffing, the Technical Report ISO/TR 13989 shall be preferably used. ISO/TR 13989 is a Technical Report (March 2000). This document is not to be regarded as an ‘International Standard’. It is proposed for provisional application so that information and experience of its use in practice may be gathered. The scuffing load capacity is calculated according to ISO/TR 13989 Part 1 (Flash temperature method) and Part 2 (Integral temperature method) as soon as you select ‘ISO 6336 Method B’.
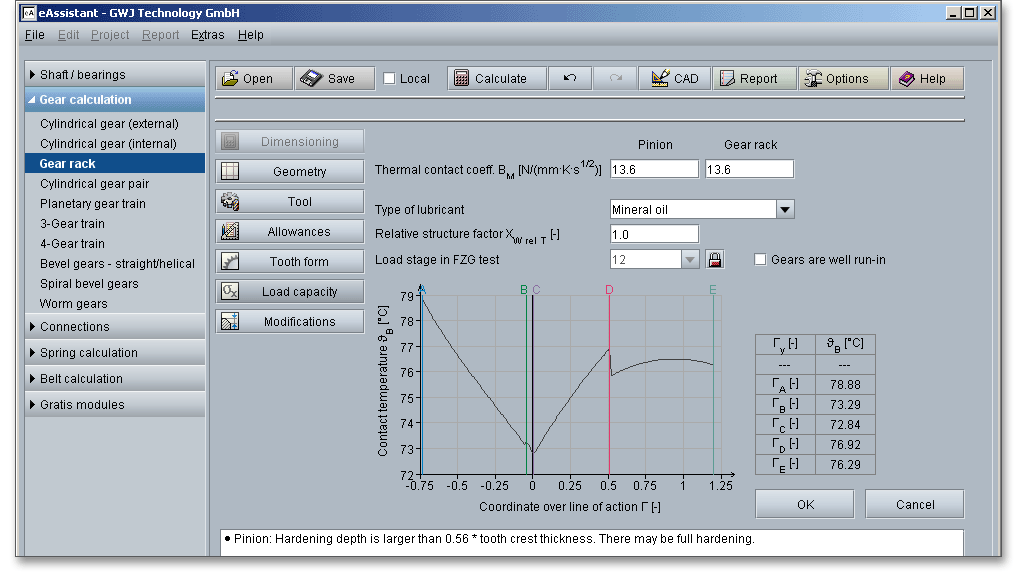
The thermal contact coefficient \(B_{M}\) is required for the determination of the flash factor. The flash factor considers
the influence of the material properties of gear and pinion on the flash temperature.
The lubricant factor \(X_{L}\) depends on the the type of lubricant. You can select the following types:
The relative structure factor \(X_{WrelT}\) is primarily intended to take into account influence of the material properties on the scuffing load capacity and is determined by:
\[X_{WrelT} = \frac {X_{W}}{X_{WT}}\]
| \(X_{W}\) | The lower table provides the empirically determined relative structure factor. |
| \(X_{WT}\) | The relative structure factor of test gears that are used for the determination of the scuffing |
| temperature. \(X_{WT}\) = 1.0 for the FZG gear test. |
| Structural Factor \(X_{W}\)9
| |
| Material/Heat Treatment | Structural Factor \(X_{W}\) |
| Through-hardened steel | 1.00 |
| Phosphated steel | 1.25 |
| Copper plated steel | 1.50 |
| Bath and gas nitrided steel | 1.50 |
| Hardened carburized steel, with austenite content: | |
| - less than average | 1.15 |
| - average (10% to 20%) | 1.00 |
| - greater than average | 0.85 |
| Austenitic steel (stainless steel) | 0.45 |
| 9 from: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag Muenchen Wien, 1996, p. 367, table 6.5/16
| |
Because scuffing is not a fatigue failure, a standard FZG gear test was developed to determine the scuffing load capacity of a lubricant under certain operating conditions. The gear test, known as FZG gear test (Institute for Machine Elements Gear Research Center, University Munich, Germany), is a standardized method according to DIN 51354. At the FZG, the different influences on scuffing are extensively investigated. The test is performed on a standard FZG test machine using standard test gears. Standardized, case-hardened and ground gears with a large one-side profile shift are used. The load is increased gradually on a FZG gear test rig with defined technical parameters. There are 12 load stages and the gears are inspected for scuffing after every load stage. Finally, the load stage is determined where scuffing of the gear teeth occurs and where the flank area is damaged by scratches. The higher the load stages, the better the industrial gear lubricants resistance to scuffing. Click the ‘Lock’ button in order to select a load stage.
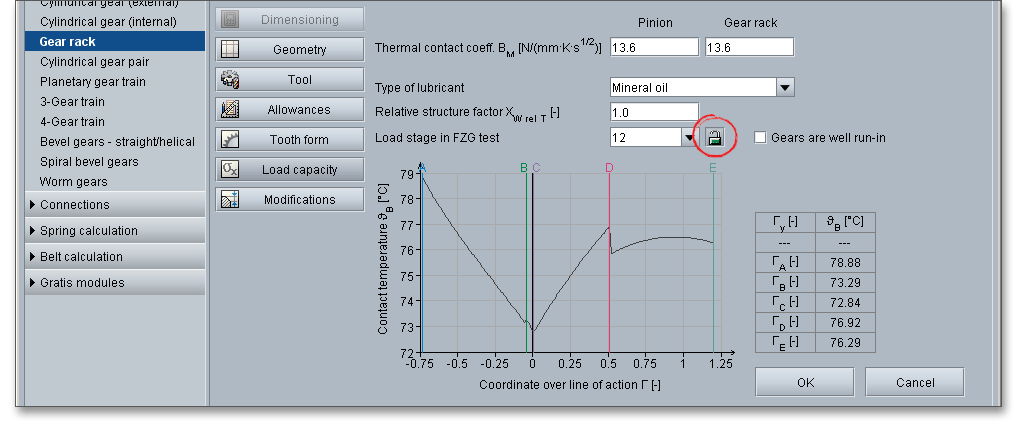
High surface temperatures due to high loads and slidings speeds can cause a lubricant film breakdown. Because of that, there are two calculation methods in ISO/TR 13989 that are based on different criteria for the development of a damage. The eAssistant software provides both the integral temperature method and flash temperature method:
The flash temperature is the temperature at which a gear-tooth surface is calculated to be hot enough to destroy the oil film and allow instantaneous welding at the contact point. The contact temperature \(\vartheta _{B}\) in any point of contact \(Y\) results from the sum of the bulk temperature \(\vartheta _{M}\) and the flash temperature \(\vartheta _{fla}\):
\[\vartheta _{B} = \vartheta _{M} + \vartheta _{fla}\]
According to the flash temperature method, there is no scuffing as long as the contact temperature \(\vartheta _{B}\) (as the sum of bulk temperature \(\vartheta _{M}\) and flash temperature \(\vartheta _{fla}\)) does not exceed the scuffing contact temperature in all points of contact. The scuffing temperature \(\vartheta _{S}\) to be a characteristic value for the material-lubricant-material system of a gear pair, to be determined by gear tests with the same material-lubricant-material system.
Please note: Points A to E mark the important points from the beginning to the end of the mesh.
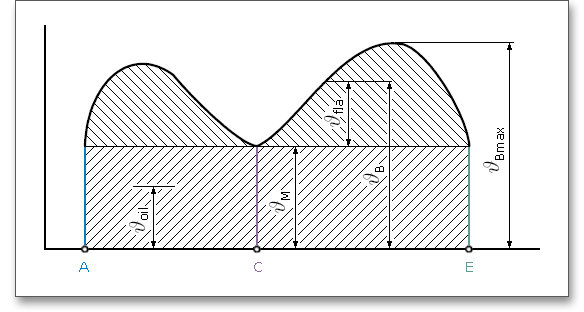
The safety against scuffing \(S_{B}\) is determined according to the flash temperature method:
\[S_{B} = \frac {\vartheta _{S} - \vartheta _{oil}}{\vartheta _{Bmax} - \vartheta _{oil}} \geq S_{Bmin}\]
| \(\vartheta _{Bmax}\) | Maximum contact temperature along the path of contact |
| \(\vartheta _{oil}\) | Oil temperature before reaching the mesh |
| \(\vartheta _{S}\) | Scuffing temperature |
The safety factor \(S_{Bmin}\) is dependent on whether the gearing is put into operation after a good running-in period. With
a careful running-in period, there is no scuffing damage up to \(S_{Bmin} \approx 1\). Without a running-in period, there is no scuffing
up to \(S_{Bmin} \approx 3\) (according to Linke).
According to the integral temperature method, scuffing occurs when the integral temperature exceeds the scuffing integral temperature. The scuffing integral temperature is assumed as a characteristic value for the material-lubricant-material system of a gear pair and is determined from gear tests. The scuffing safety according the integral temperature method \(S_{intS}\) is calculated as follows:
\[S_{intS} = \frac {\vartheta _{intS}}{\vartheta _{int}} \geq S_{Smin}\]
| \(\vartheta _{intS}\) | Scuffing integral temperature |
| \(\vartheta _{int}\) | Integral temperature |
As uncertainties and inaccuracies in the assumptions cannot be excluded, it is necessary to introduce a safety factor. According to Linke, the following reference values can be used:
| \(S_{intS} < 1.0\) | In all probability, scuffing damages are expected to occur. |
| \(1.0 \leq S_{intS} \leq 2.0\) | For a careful running-in period of the gearing, good contact pattern and real assumed |
| loads, there are no scuffing damages to be expected. |
| \(S_{intS} > 2.0\) | There is no risk of scuffing. |
The standard provides the calculation of safeties for the root and flank. Further the calculation of risk of scuffing is also available. Additional to the DIN 3990 and ISO 6336 standard, the ANSI/AGMA 2101-D04 provides also the calculation of wear. The eAssistant software calculates the wear as failure probability. Select ANSI/AGMA 2101-D04 from the listbox and the input fields are enabled. The following explains some factors from the standard.
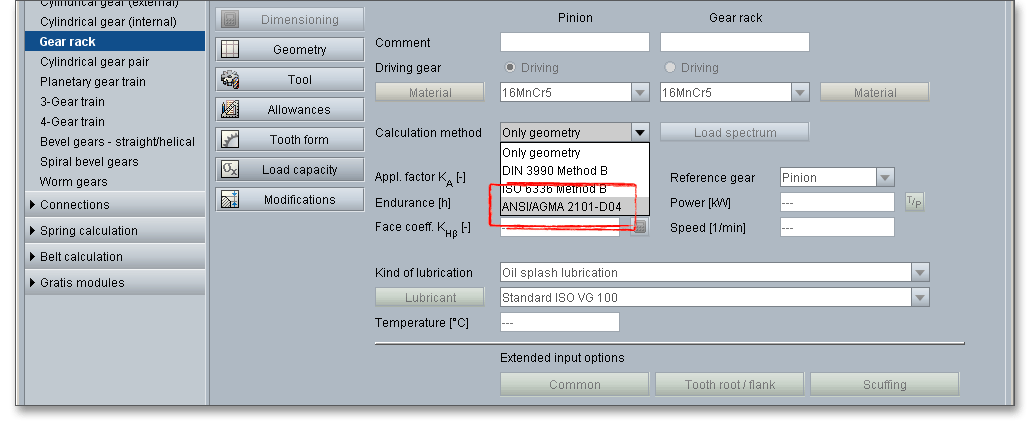
With the new edition of the ANSI/AGMA 2101-D04 (ANSI/AGMA 2001-D04 imperial unit edition, the application factor from ANSI/AGMA 2101-C95 was replaced by overload factor \(K_{O}\).

The overload factor is intended to make allowance for all externally applied loads in excess of the nominal
tangential load, \(F_{t}\), for a particular application. Overload factors can only be established after considerable field
experience is gained in a particular application.
For an overload factor of unity, this rating method includes the capacity to sustain a limited number of up
to 200 % momentary overload cycles (typically less than four starts in 8 hours, with a peak not
exceeding one second duration). Higher or more frequent momentary overloads shall be considered
separately.
In determining the overload factor \(K_{O}\), consideration should be given to the fact that many prime movers and driven
equipment, individually or in combination, develop momentary peak torques appreciably greater than those
determined by the nominal ratings of either the prime mover or the driven equipment. There are many possible
sources of overload which should be considered. Some of these are: system vibrations, acceleration torques,
overspeeds, variations in system operation, split path load sharing among multiple primemovers, and changes in
process load conditions.
The stress cycle factors, \(Z_{N}\) and \(Y_{N}\), adjust the allowable stress numbers for the required number of cycles of
operation. For the purpose of this standard, \(n_{L}\), the number of stress cycles is defined as the number of mesh
contacts, under load, of the gear tooth being analyzed.
AGMA allowable stress numbers are established for \(10^{7}\) unidirectional tooth load cycles at 99 % reliability. The
stress cycle factor adjusts the allowable stress numbers for design lives other than \(10^{7}\) cycles. The stress cycle
factor accounts for the S-N characteristics of the gear material as well as for the gradual increased tooth stress
which may occur from tooth wear, resulting in increased dynamic effects and from shifting load distributions
which may occur during the design life of the gearing.
Standard surface condition factor \(Z_{R}\) for gear teeth have not yet been established for cases where there is a
detrimental surface finish effect. In such cases, some surface finish factor greater than unity should be used.
The surface condition factor can be taken as unity provided the appropriate surface condition is
achieved.
The size factor KS reflects non-uniformity of material properties. It depends primarily on: tooth size, diameter of
parts, ratio of tooth size to diameter of part, facewidth, area of stress pattern, ratio of case depth to tooth
size, hardenability and heat treatment of materials. Standard size factors for gear teeth have not
yet been established for cases where there is a detrimental size effect. In such cases, some size
factor greater than unity should be used. The size factor may be taken as unity for most gears,
provided a proper choice of steel is made for the size of the part and its heat treatment and hardening
process.
The temperature factor \(Y_{\vartheta }\) is generally taken as unity when gears operate with temperatures of oil or gear blank not exceeding 120°C. When operating temperatures result in gear blank temperatures below 0°C, special care must be given. When operating at oil or gear blank temperature above 120°C, \(Y_{\vartheta }\) is given a value greater than 1.0 to allow for the effect of temperature on oil film and material properties. Consideration must be given to the loss of hardness and strength of some materials due to the tempering effect of temperatures over 150°C.
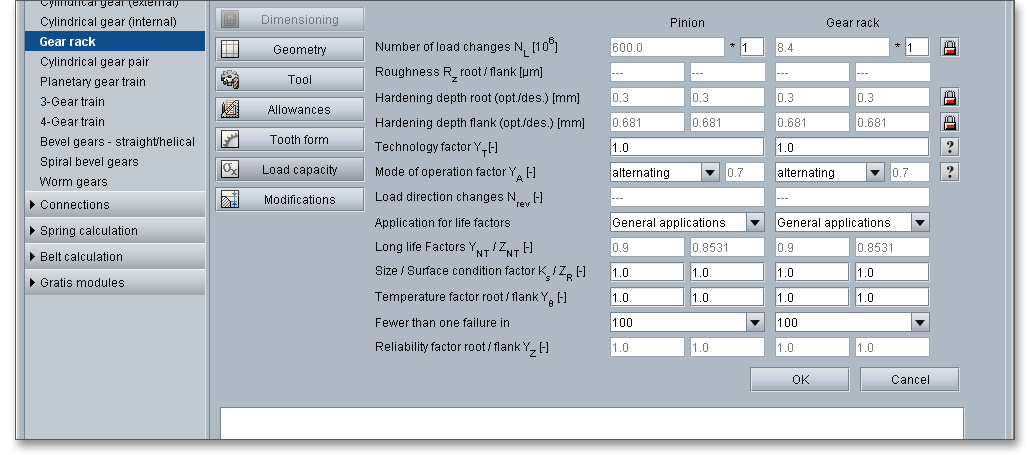
The reliability factors \(Y_{Z}\) account for the effect of the normal statistical distribution of failures found in materials testing. The allowable stress numbers given in ANSI/AGMA (tables 3 through 6) are based upon a statistical probability of one failure in 100 at \(10^{7}\) cycles. The following table contains reliability factors which may be used to modify these allowable stresses to change that probability. These numbers are based upon data developed for bending and pitting failure by the U.S. Navy. Other values may be used if specific data is available.
| Reliability Factor \(Y_{Z}\)110
| |
| Requirements of Application | \(Y_{Z}\) |
| Fewer than one failure in 10 000 | 1.50 |
| Fewer than one failure in 1000 | 1.25 |
| Fewer than one failure in 100 | 1.00 |
| Fewer than one failure in 10 | 0.852 |
| Fewer than one failure in 2 | 0.7023 |
| Notes: 1) Tooth breakage is sometimes considered a greater hazard than
pitting. In such cases a greater value of \(Y_{Z}\) is selected for bending. 2) At this value
plastic flow might occur rather than pitting. 3) From test data extrapolation.
| |
| 10 from: ANSI/AGMA 2001-D04: Fundamental Rating Factors and Calculation
Methods for Involute Spur and Helical Gear Teeth, 2016, p. 38, table 116
| |
The service factor \(C_{SF}\) has been used in previous AGMA standards to include the combined effects of overload,
reliability, life and other application related factors. This standard provides a means to account for: variations in
load (with overload factor), statistical variations in S-N data (with reliability factor), and the number of design
stress cycles (with stress cycle factor).
The AGMA service factor as traditionally used in gear applications depends on experience acquired in each
specific application. Product application standards can be a good source for the appropriate value of service
factor. Equations 28 and 29 of AGMA 2101-D04 are used to establish power ratings for unity service factor to
which established service factors may be applied using equation 30. When this is done, the stress cycle factor is
calculated using the number of cycles equivalent to a specific number of hours at a specific speed, to establish
power rating for unity service factors.
Where specific experience and satisfactory performance has been demonstrated by successful use of established service factors, values of \(Z_{N}\) and \(Y_{N}\) of 1.0 may be appropriate.
Manufacturing errors, misalignment in the assembly of the gears as well as displacement of the gears under load lead to non-uniform load carrying across the facewidth and move a significant concentration of load to the tooth edges. Intentional deviations from the involute profile (profile modification) and from the theoretical tooth trace (flank modification) are used to minimize the manufacturing inaccuracies and elastic deformations, to improve the running behavior and to reduce the noise of the gear pair.
There are different types of tooth corrections. Short and long linear or short and long circular tip and
root relief are typical tooth profile modifications. Lead crowning and end relief are common flank
modifications. These corrections tend to give better load distribution over the facewidth and can reduce the
effects of misalignment. Using profile or flank modification requires an appropriate degree of gear
accuracy. The minimum required gear manufacturing accuracy is DIN quality 7 or better. Design details
should be based on a careful estimate of the deformations and manufacturing deviations of the
gearing.
In case of gear tooth profile modification, parts of the involute profile are changed to reduce the load in that area. Profile modifications help gears to run more quietly and to regulate transmission errors.

Tip relief is a modification whereby material is removed at the tips of the gear tooth. In case of root relief, a small amount of material is removed near the root of the gear tooth. The modified tooth profile merges as continuously as possible into the theoretical tooth profile. Profile crowning can be seen as a combination of tip and root relief.
There are different types that can be chosen for the profile modification. A simple type of profile modification is
the linear tip relief on pinion and gear. However, it is also possible to execute only one gear with a tip and root
relief instead of both gears. The listbox allows to select linear and circular profile modification. The
linear relief results in the greatest material removal and thus the greatest relief in the effective flank
area.
When determining the lengths of the profile correction, a distinction is made between short and long profile modification. In case of long tip and root relief, the entire double contact area is corrected, while in the case of short execution, only half of the double contact area is removed. Either long or short reliefs are used on a gearing. The long profile modification is usually suitable for a quiet operation, while the short profile correction has better load behavior. As long as the overlap ratio is sufficient, a long profile correction is more suitable for helical gearing.
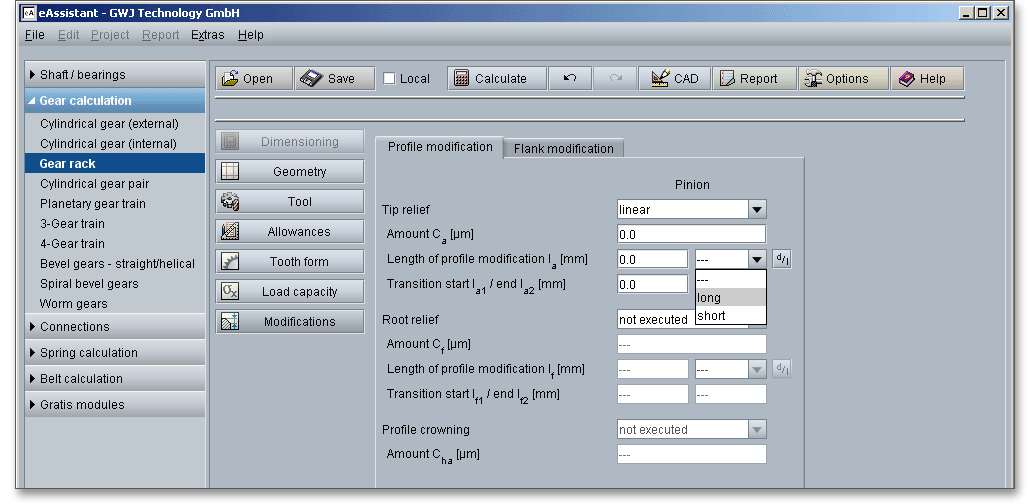
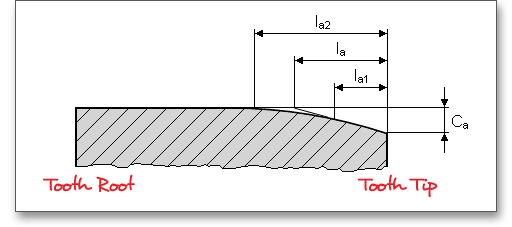
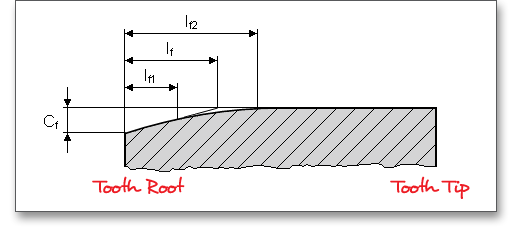
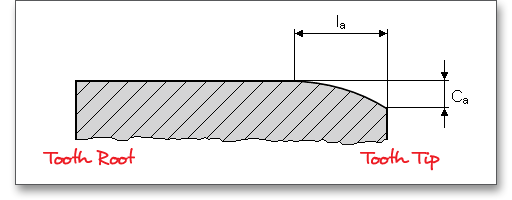
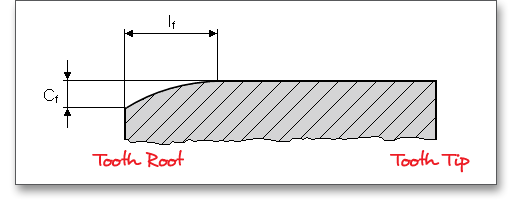
The linear tip and root relief is executed in the eAssistant with a transition rounding from the modified to the unmodified area. You can enter the start and end of the transition rounding in the corresponding input fields. For circular relief, the input of the transition start and transition end is not required.
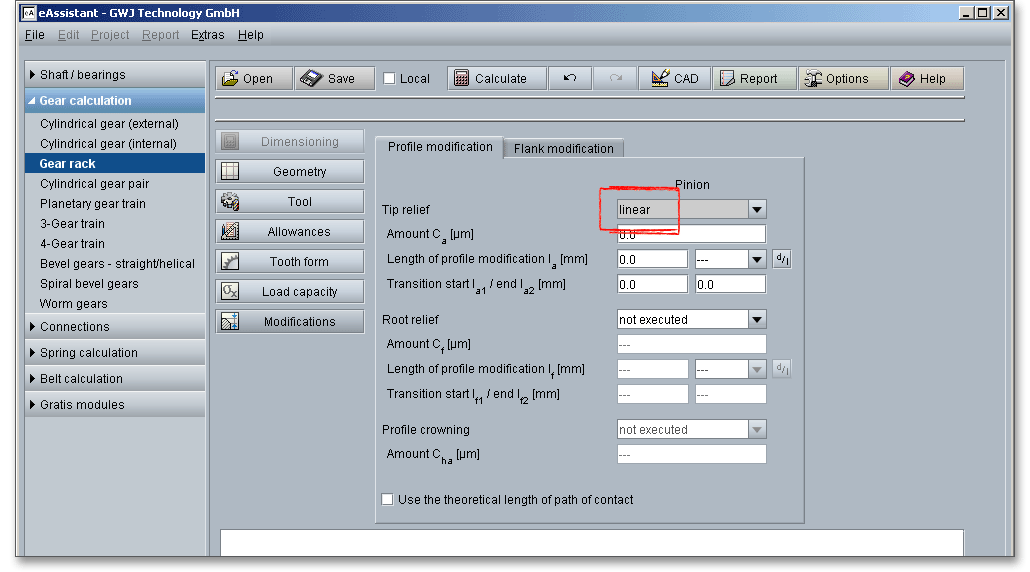
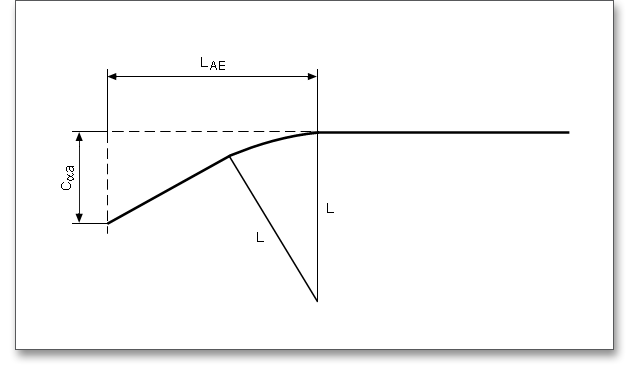
In case you know the relief length, you can simply enter this value into the input field. In case the length is unknown, select ‘short’ or ‘long’ from the listbox. The eAssistant software determines the relief length automatically. If a diameter is given on the drawing, it is possible to define the diameter. Click the ‘d/l’ button on the right side to switch between the input for diameter or length.
When you enable the checkbox ‘Use theoretical length of path of contact’, then the theoretical path of contact of a gear with a rack is used.
Profile crowning can be seen as a combination of tip relief and root relief. Material is removed from the tip and from the root of the tooth.
You can select symmetric profile crowning from the listbox and add a value for \(C_{ha}\) to the input field.
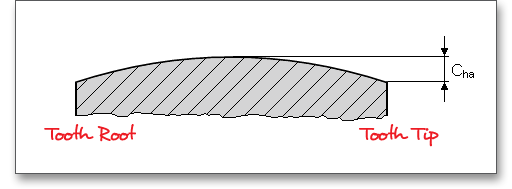
Gear flank modifications are intentional deviations from the theoretical tooth trace. Lead crowning and end relief are typical gear flank modifications and are advantageous for a better load distribution across the facewidth of the gear. Both can compensate for misalignment so that the stresses do not rise at the tooth ends.
Due to mesh misalignments, an overloading of the tooth ends occurs. Therefore, end relief is used to protect the tooth ends from overloading. Usually, the relief applied is the same at both ends of the teeth. In case crown shaving and crown grinding are not possible, then end relief is recommended.
End relief can be applied to both tooth ends or to the left or right end of the tooth.

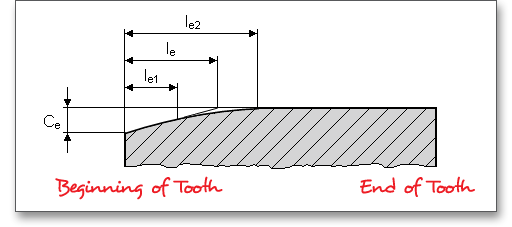
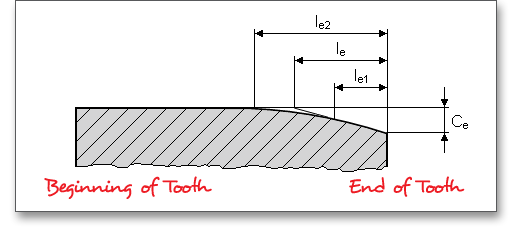
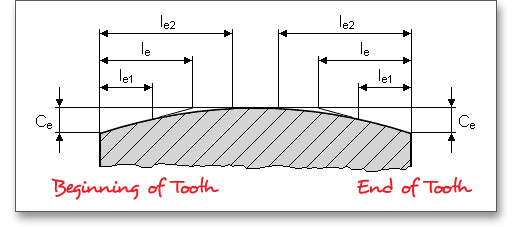
According to DIN 3990 Part 1, the height of end relief is calculated as follows:
For through-hardened gears: \(C_{e} \approx F_{\beta xcv}\) plus a manufacturing tolerance of 5 to 10 \(\mu m\). Thus, by analogy with \(F_{\beta xcv}\) (initial equivalent misalignment) in DIN 3990, \(C_{e}\) should be approximately:
\[C_{e} = f_{sh} + 1,5 \cdot f_{H\beta }\]
For surface hardened and nitrided gears: \(C_{e} \approx 0,5 \cdot F_{\beta x cv}\) plus a manufacturing tolerance of 5 to 10 \(\mu m\).
\(C_{e}\)should be approximately:
\[C_{e} = 0,5 \cdot (f_{sh} + 1,5 \cdot f_{H\beta })\]
When the gears are of such stiff construction that \(f_{sh}\) can for all practical purposes be neglected or when the helices have been modified to compensate deformation, the following is appropriate:
\[C_{e} = f_{H\beta }\]
60% to 70% of the above values is appropriate for very accurate and reliable gears with high tangential velocities.
According to DIN 3990 Part 1, the width (or length) of end relief can be determined as follows:
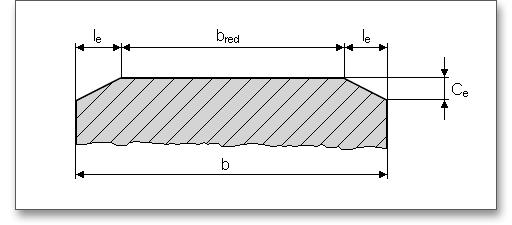
For approximately constant loading and higher tangential velocities:
\(l_{e}\)= kleinerer Wert von \(0,1 \cdot b\) oder \(1 \cdot m\)
The following is appropriate for variable loading, low and average speeds:
\[b_{red} = (0,5\ to\ 0,7) \cdot b\]
Lead crowning is a common way of crowning is the so-called lead crowning. This type is employed in order to compensate for manufacturing deviations and load-induced deformations of the gears and in particular to relieve the tooth-endloading.
Gears are usually crowned symmetrically about the mid-facewidth and the tooth center is slightly thicker than the tooth edges. The tooth flanks of the gear have a slight outward bulge in its center area. It is possible to select symmetrical and asymmetrical lead crowning from the listbox.
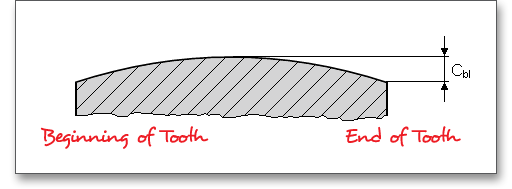
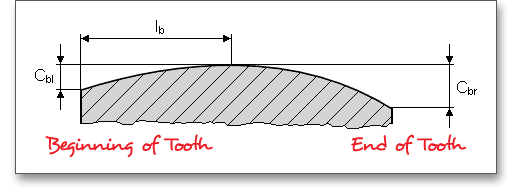
According to DIN 3990 Part 1, the height of lead crowning can be determined as follows:
\[C_{b} = 0,5 \cdot (f_{sh} + 1,5 \cdot f_{H\beta })\]
When the gears are of such stiff construction that \(f_{sh}\) can for all practical purposes be neglected or when the helices have been modified to compensate for deformation at mid-face width, the following value can be substituted:
\[C_{b} = f_{H\beta }\]
Subject to the restriction \(10 \leq C_{b} \leq 25\ \mu m\) plus a manufacturing tolerance of about 5 \(\mu m\), 60% to 70% of the above values are adequate for extremely accurate and reliable high speed gears.
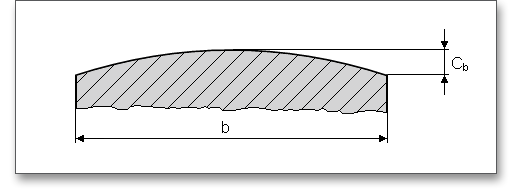
According to DIN 3990, the mesh misalignment \(f_{sh}\) is determined without taking crowning into account. This means that in the calculation of the load capacity (submask \(K_{H\beta }\), ‘no correction’ must be set. With regard to the suggested value of lead crowning calculated according to DIN 3990, it is always a value related to the effective sum of the modifications of pinion and gear in the contact area. This means that the modifications can only be carried out on one gear or divided between the pair. Therefore, the default value calculation for gear 1 and 2 always provides the same value. How this calculated value is then divided, if necessary, is decided by the user. If the value is first suggested for gear 1, it can then be divided between gear 1 and gear 2. This also applies to gear 2. When splitting the crowning amount between both gears, there are various distribution ratios. Often, the following approach is used here:
\[C_{b}^{2} = C_{b1}^{2} + C_{b2}^{2}\]
Therefore, only the value for the pairing is always generated as a default value via the calculator
button.
If parts of the flank of gear and mating gear mesh outside of the path of contact or if the contact ratio is \(\epsilon _{\gamma } < 1\), then meshing interferences may occur. A large profile shift as well as a very small tip clearance may cause meshing interferences. Interference takes place between the tip of the tooth of the gear and root fillet area of the mating tooth. In some cases, the interference may be eliminated by decreasing the addendum of only one gear teeth. Due to meshing interferences, operating noise, gear failure (e.g., tooth breakage) and an increased wear can occur. In case of a basic rack profile, meshing interferences can be manipulated or removed by the following:
To assure smooth continuous tooth action, a pair of teeth must already have come into engagement. Especially for spur gear pairs a low contact ratio can appear:
The condition for a smooth and continuous tooth action is:
\[\epsilon _{\gamma } = \epsilon _{\alpha } + \epsilon _{\beta } > 1\]
The result panel displays the total contact ratio. In case the condition \(\epsilon _{\gamma } = \epsilon _{\alpha } + \epsilon _{\beta } > 1\) is not fulfilled, the total contact ratio will be
marked in red. Furthermore, you will get an appropriate warning in the message window.
The calculation module provides a message window. This message window displays detailed information, helpful hints or warnings about problems. One of the main benefits of the program is that the software provides suggestions for correcting errors during the data input. If you check the message window carefully for any errors or warnings and follow the hints, you are able to find a solution to quickly resolve calculation problems.

The quick info tooltip provides additional information about all input fields and buttons. Move the mouse pointer over the input field or button, then you will get the additional information. This information will be displayed in the quick info line.
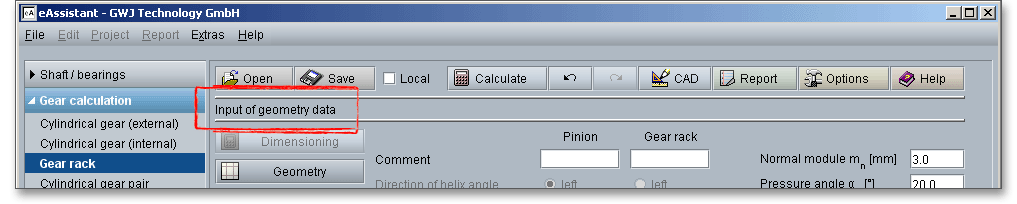
All results will be calculated during every input and will be displayed in the result panel. A recalculation occurs after every data input. Any changes that are made to the user interface take effect immediately. In case a minimum safety is not fulfilled, the result will be marked red. Press the Enter key or move to the next input field to complete the input. Alternatively, use the Tab key to jump from field to field or click the ‘Calculate’ button after every input. Your entries will be also confirmed and the calculation results will displayed automatically.

After the completion of your calculation, you can create a calculation report. Click on the ‘Report’ button.

The calculation report contains a table of contents. You can navigate through the report via the table of contents that provides links to the input values, results and figures.
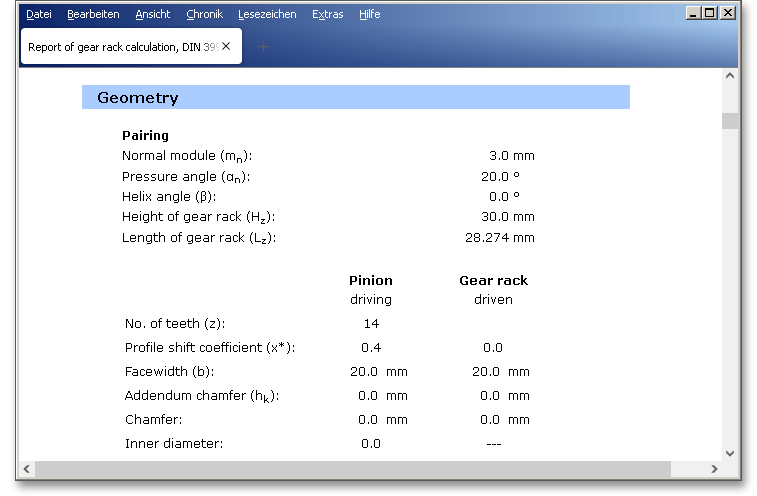
The report is available in HTML and PDF format. Calculation reports, saved in HTML format, can be opened in a web browser or in Word for Windows. You may also print or save the calculation report:
When the calculation is finished, it is easy to save the calculation. You can save your calculation either to the eAssistant server or to your computer. Click on the button ‘Save’.

Before you can save the calculation to your computer, you need to activate the checkbox ‘Local’ in the calculation module. A standard Windows dialog for saving files will appear. Now you will be able to save the calculation to your computer.
In case you do not activate the option in order to save your files locally, then a new window is opened and you can save the calculation to the eAssistant server. Please enter a name into the input field ‘Filename’ and click on the button ‘Save’.
The ‘Undo’ button allows you to reset your inputs to an older state. The ‘Redo’ button reverses the undo.

The top menu bar of the eAssistant software provides the button ‘CAD’.

The eAssistant plugin for various CAD systems (e.g., SOLIDWORKS, Solid Edge or Autodesk Inventor) enables
you to combine calculation and design very easily. On the basis of the eAssistant calculation, you can generate
spur gears in a 2D DXF format or create as a 3D part within seconds.
Click on the menu item ‘CAD \(\Rightarrow \) DXF Output’. Now you are able to create the accurate tooth form of any involute gearing in the 2D DXF format. Use the various settings for the DXF output.
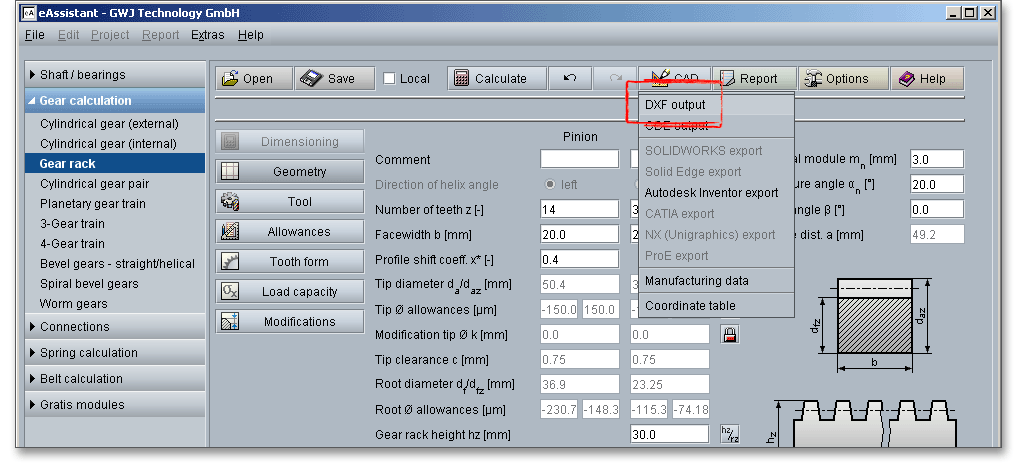
For the DXF output the following options are possible:
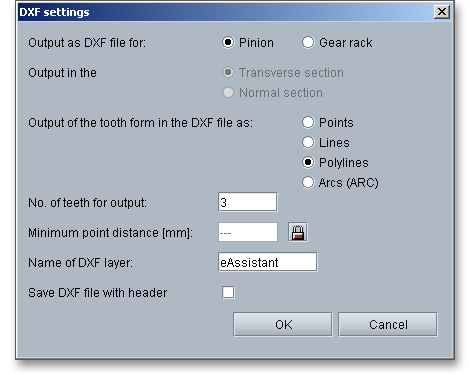
When you have defined all settings, then click on the button ‘OK’. A standard Windows dialog is opened to save the file.
Now you can save the DXF file to your computer. Enter a name for the file and click on the button ‘Save’. It is not
necessary to specify the file extension. The file is identified automatically.
With the integration of the standardised GDE format into the modules for gears and involute splines, eAssistant takes a step closer to a seamless data workflow. GDE stands for Gear Data Exchange. This format, which is defined in VDI/VDE guideline 2610, is already supported by many measuring machine manufacturers. With the GDE format, geometries of cylindrical gears and involute splines can be loaded directly from the software into the measuring machine. It only takes a few clicks to create a measuring program. This avoids transmission errors and allows to work with standard measuring instructions.

The eAssistant plugin for various CAD systems (e.g., SOLIDWORKS, Solid Edge, Autodesk Inventor) enables you to combine calculation and design very easily and fast. Based on your eAssistant calculation, you can generate external and internal spur and helical gears as a 3D part within seconds. A single menu pick in the eAssistant software transfers the eAssistant calculation data to the CAD system. Based on these parameters, the automatic creation of a 3D parametric model starts in the CAD system. Allowances, addendum chamfer, profile shift and profile modifications (tip and root relief) are taken into consideration.
The CAD model stores all features and dimensions as design parameters. The eAssistant calculation is linked
and associated to the part and can be opened at any time throughout the entire design phase.
This is also possible if one part contains different calculations. Click the button ‘CAD’ and select
the CAD plugin. Open the CAD system and start the generation by clicking the integrated button
‘eAssistant’.
Please note: First you need to download and install the right CAD plugin for your CAD system. The plugin is
available on our web site www.eAssistant.eu. After installation, an integrated button called ‘eAssistant’ appears
in the CAD system.
With just one click, the design table with all manufacturing details can be placed on the drawing. The appearance and size of that table is individually configurable. There is no need to manually add all design table parameters to the drawing. For further information, please visit our web site www.eAssistant.eu or read the manual.
The button ‘CAD \(\Rightarrow \) Manufacturing data’ allows to save the manufacturing data to a text file.
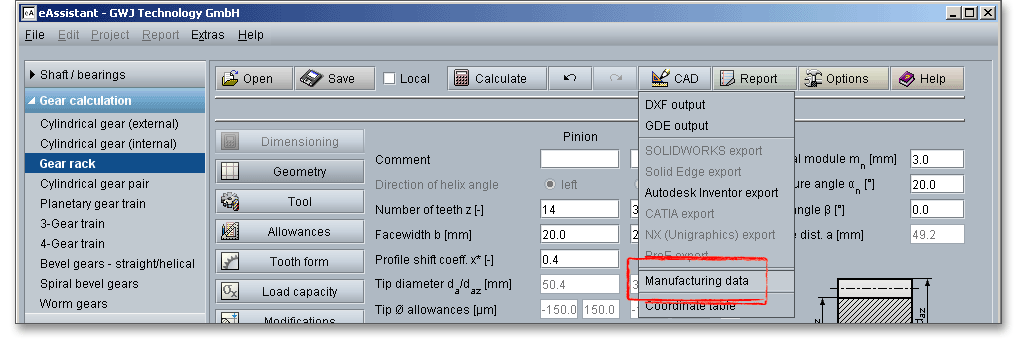
The gear tooth form geometry of a tooth space can be exported as a coordinate text file in transverse section as well as in normal section.
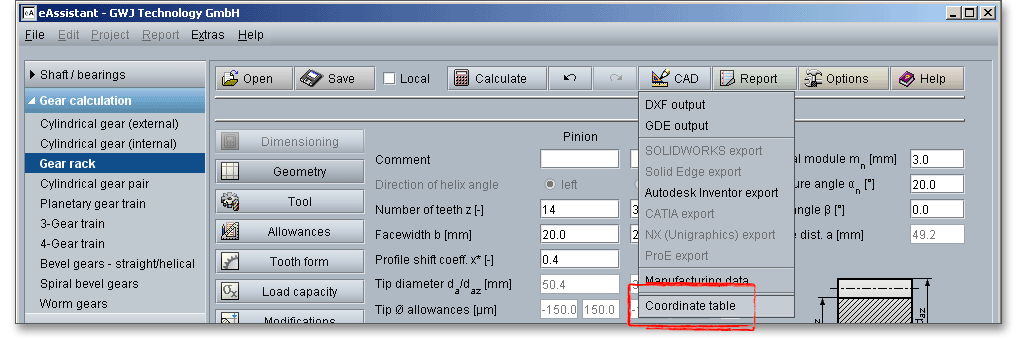
Click on the button ‘Options’ in the top menu bar of the eAssistant software.

This option allows you to change some general settings: